
题目列表(包括答案和解析)
有一项符合要求的
1.已知全集U=R,集合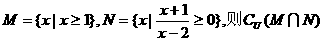
A.{x|x<2} B.{x|x≤2} C.{x|-1<x≤2} D.{x|-1≤x<2}
(17)(本小题满分12分)
已知平面内三点A(3,0),B(0,3),C(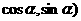 ,O为坐标原点.
,O为坐标原点.
(1) 若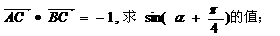
(2) 若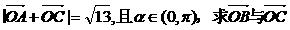 的夹角。
的夹角。
(18)(本小题满分12分)
盒子中装着有标数字1,2,3,4,5的上卡片各2张,从盒子中任取3张卡片,每张卡片被取出的可能性都相等,用 表示取出的3张卡片上的最大数字,求:
表示取出的3张卡片上的最大数字,求:
(1)取出的3张卡片上的数字互不相同的概率;
(2)随机变量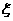 的概率分布和数学期望;
的概率分布和数学期望;
(19)(本小题满分12分)
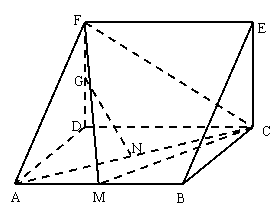 如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF
如图,在三棱柱BCE-ADF中,四边形ABCD是正方形,DF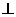 平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
平面ABCD,M、N分别是AB、AC的中点,G是DF上的一点.
(1)求证: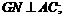
(2)若FG=GD,求证:GA//平面FMC.
(3)若DF=DA,求二面角F-MC-D的正弦值
(20)(本小题满分12分)
设椭圆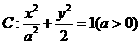 的左右焦点分别为
的左右焦点分别为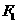 、
、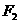 ,
, 是椭圆
是椭圆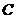 上的一点,且
上的一点,且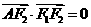 ,坐标原点
,坐标原点 到直线
到直线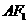 的距离为
的距离为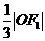 .
.
(Ⅰ)求椭圆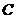 的方程;
的方程;
(Ⅱ)设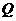 是椭圆
是椭圆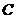 上的一点,过点
上的一点,过点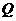 的直线
的直线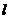 交
交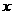 轴于点
轴于点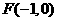 ,交
,交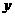 轴于点
轴于点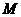 ,若
,若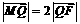 ,求直线
,求直线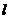 的斜率.
的斜率.
(21)(本小题满分12分)
已知函数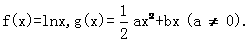
(I)若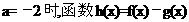 在其定义域是增函数,求b的取值范围;
在其定义域是增函数,求b的取值范围;
(II)在(I)的结论下,设函数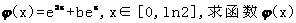 的最小值;
的最小值;
(III)设函数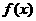 的图象C1与函数
的图象C1与函数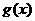 的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
的图象C2交于点P、Q,过线段PQ的中点R作x轴的垂线分别交C1、C2于点M、N,问是否存在点R,使C1在M处的切线与C2在N处的切线平行?若存在,求出R的横坐标;若不存在,请说明理由.
 (22) 请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
(22) 请考生在A、B、C三题中任选一题作答,如果多做,则按所做的第一题记分。作答时,用2B铅笔在答题卡上把所选题目对应的标号涂黑。
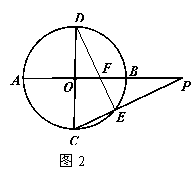
(22) A (本小题满分10分)选修4-1:几何证明选讲
如图2所示,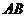 与
与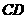 是⊙O的直径,
是⊙O的直径,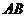
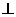
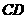 ,
,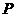 是
是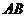 延长线上一点,连
延长线上一点,连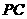 交⊙O于点
交⊙O于点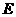 ,连
,连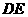 交
交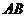 于点
于点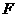 ,若
,若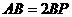 .
.
求证: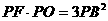
(22) B (本小题满分10分)选修4-4:坐标系与参数方程
在曲线 :
: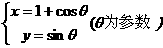 上求一点,使它到直线
上求一点,使它到直线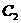 :
: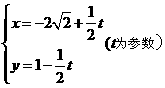 的距离最小,并求出该点坐标和最小距离。
的距离最小,并求出该点坐标和最小距离。
.
(22) C (本小题满分10分)选修4-5:不等式选讲
若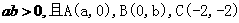 三点共线,求
三点共线,求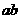 的最小值。
的最小值。
08高考理科数学第二次月考模拟试题
(13)若命题“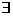 x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
x∈R,使x2+(a-1)x+1<0”是假命题,则实数a的取值范围为
.
(14)在区间[1, 5 ]上分别取一个实数,记为m ,则方程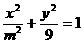 表示焦点在x轴上的椭圆的概率是____________________
表示焦点在x轴上的椭圆的概率是____________________
(15)若三角形内切圆半径为 ,三边长分别为
,三边长分别为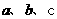 ,则三角形的面积
,则三角形的面积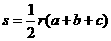 ,根据类比思想,若四面体内切球半径为
,根据类比思想,若四面体内切球半径为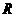 ,其四个面的面积分别为
,其四个面的面积分别为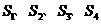 ,则四面体的体积
,则四面体的体积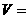 ________
________
(16)某小卖部为了了解热茶销售量y(杯)与气温x(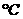 )之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
)之间的关系,随机统计了某4天卖出的热茶的杯数与当天气温,并制作了对照表:
气温x(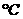 ) ) |
18 |
13 |
10 |
-1 |
|
杯数y |
24 |
34 |
38 |
64 |
由表中数据算得线性回归方程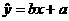 中的
中的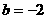 ,预测当气温为
,预测当气温为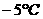 时,热茶销售量为____杯.(回归系数
时,热茶销售量为____杯.(回归系数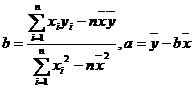 )
)
22.在f(m,n)中,m、n、f(m,n)均为非负整数,且对任何m,n有:
(Ⅰ)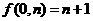 ;
;
(Ⅱ)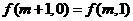 ;
;
(Ⅲ)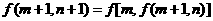
试求:(I)f(1,0)的值;
(II)f(1,n)关于n的表达式;
(III)f(3,n)关于n的表达式.
20.(本小题满分12分)已知函数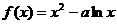 在(1,2
在(1,2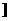 是增函数,
是增函数,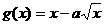 在(0,1)为减函数.
在(0,1)为减函数.
(Ⅰ)求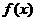 、
、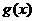 的表达式;
的表达式;
(Ⅱ)求证:当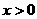 时,方程
时,方程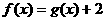 有唯一解.
有唯一解.
 21.在△ABC中,sinA、sinB、sinC构成公差为正的等差数列,且其周长为12.以
21.在△ABC中,sinA、sinB、sinC构成公差为正的等差数列,且其周长为12.以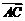 为x轴,AC的中垂线为y轴建立直角坐标系xoy.
为x轴,AC的中垂线为y轴建立直角坐标系xoy.
(Ⅰ)证明存在两个定点E、F,使得|BE|+|BF|为定长;
并求出点E、F的坐标及点B的轨迹Γ;
(Ⅱ)设P为轨迹Γ上的任一点,点M、N分别在射线
PA、PC上,动点Q满足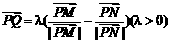 ,
,
经过点A且以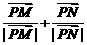 为方向向量的直线与动
为方向向量的直线与动
点Q的轨迹交于点R,试问:是否存在一个定点D,
使得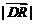 为定值?若存在,求出点D的坐标;若不存在,说明理由?
为定值?若存在,求出点D的坐标;若不存在,说明理由?
19.(本小题满分12分)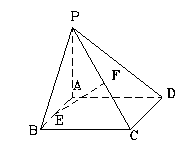 在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
在四棱锥P-ABCD中,底面ABCD是矩形,侧棱PA垂直于底面,E、F分别是AB、PC的中点.
(I)求证: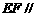 平面PAD;
平面PAD;
(II)当平面PCD与平面ABCD成多大二面角时,
直线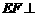 平面PCD?
平面PCD?
18.(本小题满分12分)某次有奖竞猜活动中,主持人准备了A、B两个相互独立的问题, 并且宣布:观众答对问题A可获奖金a元,答对问题B可获奖金2a元;先答哪个题由观众自由选择;只有第1个问题答对,才能再答第2个问题,否则中止答题。若你被选为幸运观众,且假设你答对问题A、B的概率分别为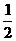 、
、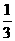 .你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由.
.你觉得应先回答哪个问题才能使你获得奖金的期望较大?说明理由.
17.(本小题满分12分)已知函数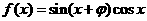 的图像关于原点
的图像关于原点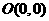 对称,试求函数
对称,试求函数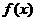 的解析式.
的解析式.
16.若连续且不恒等于的零的函数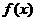 满足
满足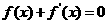 ,试写出一个符合题意的函数
,试写出一个符合题意的函数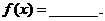
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com