
题目列表(包括答案和解析)
6.下列命题中,正确的是( C )
A.若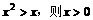 B.若
B.若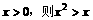
C.若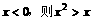 D.若
D.若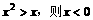
5.若全集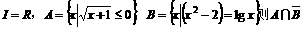 是( B )
是( B )
A.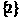 B.
B.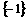 C.
C.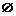 D.
D.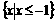
4.三个数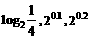 的大小关系是 ( B )
的大小关系是 ( B )
(A)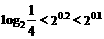 (B)
(B)
(C)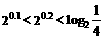 (D)
(D)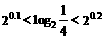
3.不等式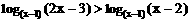 成立的一个充分但不必要条件是 ( B )
成立的一个充分但不必要条件是 ( B )
(A)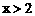 (B)
(B)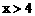 (C)
(C)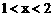 (D)
(D)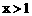
2.当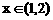 时,不等式
时,不等式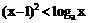 恒成立,则
恒成立,则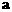 的取值范围是( B
)
的取值范围是( B
)
(A)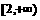 (B)(1,2) (C)
(B)(1,2) (C)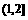 (D)(0,1)
(D)(0,1)
[不等式的解法练习1]
1.不等式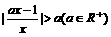 的解集是 ( D )
的解集是 ( D )
(A){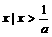 }
(B){
}
(B){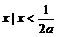 }
}
(C){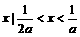 }
(D){
}
(D){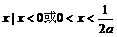 }
}
不等式的解法
[例1]
解不等式: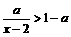
解:原不等式可化为: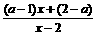 >0,
>0,
即[(a-1)x+(2-a)](x-2)>0.
当a>1时,原不等式与(x-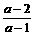 )(x-2)>0同解.
)(x-2)>0同解.
若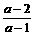 ≥2,即0≤a<1时,原不等式无解;若
≥2,即0≤a<1时,原不等式无解;若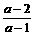 <2,即a<0或a>1,于是a>1时原不等式的解为(-∞,
<2,即a<0或a>1,于是a>1时原不等式的解为(-∞,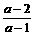 )∪(2,+∞).
)∪(2,+∞).
当a<1时,若a<0,解集为(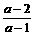 ,2);若0<a<1,解集为(2,
,2);若0<a<1,解集为(2,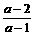 )
)
综上所述:
当a>1时解集为(-∞,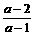 )∪(2,+∞);
)∪(2,+∞);
当0<a<1时,解集为(2,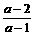 );
);
当a=0时,解集为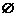 ;
;
当a<0时,解集为(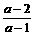 ,2).
,2).
[例2]
设不等式x2-2ax+a+2≤0的解集为M,如果M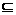 [1,4],求实数a的取值
[1,4],求实数a的取值
范围.
解:M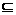 [1,4]有n种情况:其一是M=
[1,4]有n种情况:其一是M=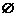 ,此时Δ<0;其二是M≠
,此时Δ<0;其二是M≠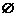 ,此时Δ>0,分三种情况计算a的取值范围.
,此时Δ>0,分三种情况计算a的取值范围.
设f(x)=x2 -2ax+a+2,有Δ=(-2a)2-(4a+2)=4(a2-a-2)
(1)当Δ<0时,-1<a<2,M=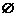
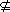 [1,4]
[1,4]
(2)当Δ=0时,a=-1或2.当a=-1时M={-1}?[1,4];当a=2时,m={2}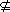 [1,4].
[1,4].
(3)当Δ>0时,a<-1或a>2.设方程f(x)=0的两根x1,x2,且x1<x2,那么M=[x1,x2],M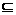 [1,4]
[1,4] 1≤x1<x2≤4
1≤x1<x2≤4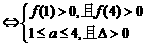
即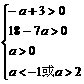 ,解得:2<a<
,解得:2<a<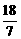 ,
,
∴M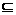 [1,4]时,a的取值范围是(-1,
[1,4]时,a的取值范围是(-1,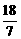 ).
).
[例3]
解关于x的不等式: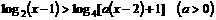 .
.
解:原不等式等价于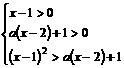 ①,即
①,即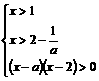 .
.
由于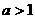 ,所以
,所以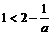 ,所以,上述不等式等价于
,所以,上述不等式等价于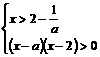 ②
②
解答这个含参数的不等式组,必然需要分类讨论,此时,分类的标准的确定就成了解答的关键.如何确定这一标准?
(1)当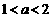 时,不等式组②等价于
时,不等式组②等价于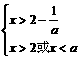
此时,由于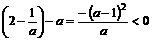 ,所以
,所以 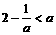 .
.
从而 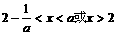 .
.
(2)当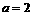 时,不等式组②等价于
时,不等式组②等价于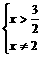
所以 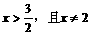 .
.
(3)当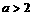 时,不等式组②等价于
时,不等式组②等价于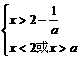
此时,由于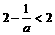 ,所以,
,所以,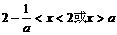 .
.
综上可知:
当 时,原不等式的解集为
时,原不等式的解集为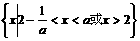 ;
;
当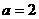 时,原不等式的解集为
时,原不等式的解集为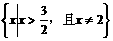 ;
;
当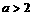 时,原不等式的解集为
时,原不等式的解集为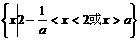 .
.
[例4]
解关于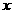 的不等式:
的不等式: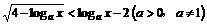
解:原不等式等价于
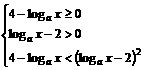
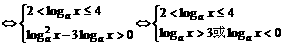
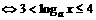 ,∴当
,∴当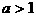 时,原不等式的解集为
时,原不等式的解集为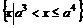
当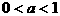 时,原不等式的解集为
时,原不等式的解集为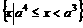
[例5]
设函数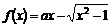 ,
,
(1)当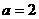 时,解不等式
时,解不等式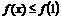 ;
;
(2)求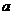 的取值范围,使得函数
的取值范围,使得函数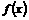 在
在 上为单调函数.
上为单调函数.
讲解:(1)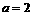 时,
时,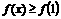 可化为:
可化为: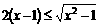 ,等价于:
,等价于:
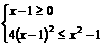 ① 或
① 或 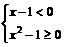 ②
②
解①得 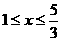 ,解②得
,解②得 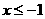 .
.
所以,原不等式的解集为
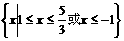 .
.
(2)任取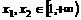 ,且
,且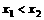 ,则
,则
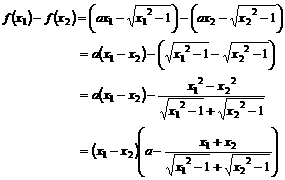
要使函数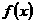 在
在 上为单调函数,需且只需:
上为单调函数,需且只需:
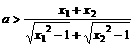 恒成立,(或
恒成立,(或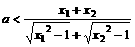 恒成立).
恒成立).
因此,只要求出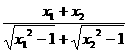 在条件“
在条件“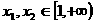 ,且
,且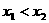 ”之下的最大、最小值即可.为了探求这个代数式的最值,我们可以考虑极端情况,如:
”之下的最大、最小值即可.为了探求这个代数式的最值,我们可以考虑极端情况,如: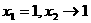 ,容易知道,此时
,容易知道,此时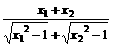
 ;若考虑
;若考虑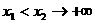 ,则不难看出,此时
,则不难看出,此时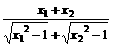
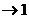 ,至此我们可以看出:要使得函数
,至此我们可以看出:要使得函数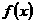 为单调函数,只需
为单调函数,只需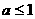 .
.
事实上,当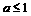 时,由于
时,由于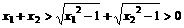 恒成立,所以,
恒成立,所以,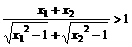 .所以,在条件“
.所以,在条件“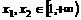 ,且
,且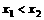 ”之下,必有:
”之下,必有: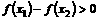 .
.
所以,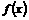 在区间
在区间 上单调递减.
上单调递减.
当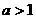 时,由(1)可以看出:特例
时,由(1)可以看出:特例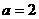 的情况下,存在
的情况下,存在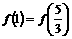 .由此可以猜想:函数
.由此可以猜想:函数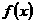 在区间
在区间 上不是单调函数.为了说明这一点,只需找到
上不是单调函数.为了说明这一点,只需找到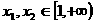 ,使得
,使得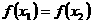 即可.简便起见,不妨取
即可.简便起见,不妨取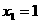 ,此时,可求得
,此时,可求得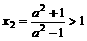 ,也即:
,也即: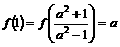 ,所以,
,所以,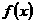 在区间
在区间 上不是单调函数.
上不是单调函数.
另解: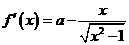 ,对
,对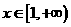 ,易知:
,易知:
当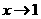 时,
时,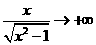 ;当
;当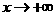 时,
时,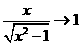 ;
;
所以当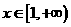 时,
时,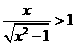 ,
,
从而只须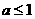 ,必有
,必有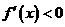 ,函数在
,函数在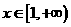 上单调递减。
上单调递减。
[例6] 已知f(x)是定义在[-1,1]上的奇函数,且f(1)=1,若m、n∈[-1,1],
m+n≠0时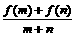 >0.
>0.
(1)用定义证明f(x)在[-1,1]上是增函数;
(2)解不等式:f(x+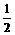 )<f(
)<f(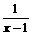 );
);
(3)若f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,求实数t的取值范围.
解:(1)证明:任取x1<x2,且x1,x2∈[-1,1],
则f(x1)-f(x2)=f(x1)+f(-x2)=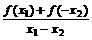 ·(x1-x2)
·(x1-x2)
∵-1≤x1<x2≤1,
∴x1+(-x2)≠0,由已知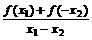 >0,又 x1-x2<0,
>0,又 x1-x2<0,
∴f(x1)-f(x2)<0,即f(x)在[-1,1]上为增函数.
(2)解:∵f(x)在[-1,1]上为增函数,
∴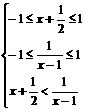 解得:{x|-
解得:{x|-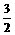 ≤x<-1,x∈R}
≤x<-1,x∈R}
(3)解:由(1)可知f(x)在[-1,1]上为增函数,且f(1)=1,
故对x∈[-1,1],恒有f(x)≤1,
所以要f(x)≤t2-2at+1对所有x∈[-1,1],a∈[-1,1]恒成立,
即要t2-2at+1≥1成立,故t2-2at≥0,
记g(a)=t2-2at,对a∈[-1,1],g(a)≥0,
只需g(a)在[-1,1]上的最小值大于等于0,
g(-1)≥0,g(1)≥0,解得,t≤-2或t=0或t≥2.
∴t的取值范围是:{t|t≤-2或t=0或t≥2}.
[例7]
给出一个不等式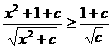 (x∈R)。
(x∈R)。
经验证:当c=1, 2, 3时,对于x取一切实数,不等式都成立。
试问:当c取任何正数时,不等式对任何实数x是否都成立?若能成立,请给出证明;若不成立,请求出c的取值范围,使不等式对任何实数x都能成立。
解:令f(x)=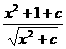 ,设u=
,设u=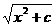 (u≥
(u≥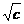 )
)
则f(x)=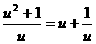 (u≥
(u≥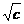 )
)
∴f(x)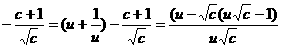
要使不等式成立,即f(x)-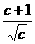 ≥0
≥0
∵u≥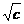 >0 ∴只须u
>0 ∴只须u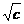 -1≥0
-1≥0
∴u2c≥1 u2≥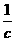 ∴x2+c≥
∴x2+c≥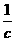
∴x2≥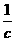 -c 故当c=
-c 故当c=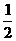 时,
时,
原不等式不是对一切实数x都成立,即原不等式对一切实数x不都成立
要使原不等式对一切实数x都成立,即使x2≥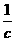 -c对一切实数都成立。
-c对一切实数都成立。
∵x2≥0 故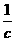 -c≤0
-c≤0
∴c≥1(c>0) ∴c≥1时,原不等式对一切实数x都能成立。
不等式的证明
[例1]
已知 ,求证:
,求证: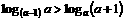
解1: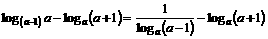
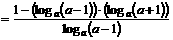 .
.
因为 ,所以,
,所以,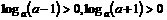 ,所以,
,所以,
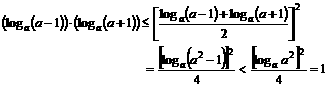
所以,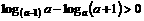 ,命题得证.
,命题得证.
解2:因为 ,所以,
,所以,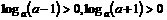 ,所以,
,所以,
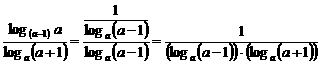 ,
,
由解1可知:上式>1.故命题得证.
[例2]
已知a>0,b>0,且a+b=1。求证:(a+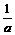 )(b+
)(b+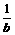 )≥
)≥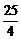 .
.
证法一:(分析综合法)
欲证原式,即证4(ab)2+4(a2+b2)-25ab+4≥0,即证4(ab)2-33(ab)+8≥0,
即证ab≤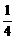 或ab≥8.
或ab≥8.
∵a>0,b>0,a+b=1,∴ab≥8不可能成立
∵1=a+b≥2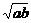 ,∴ab≤
,∴ab≤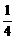 ,从而得证.
,从而得证.
证法二:(均值代换法)
设a=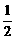 +t1,b=
+t1,b=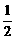 +t2.
+t2.
∵a+b=1,a>0,b>0,∴t1+t2=0,|t1|<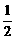 ,|t2|<
,|t2|<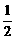
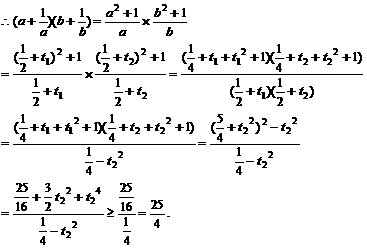
显然当且仅当t=0,即a=b=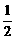 时,等号成立.
时,等号成立.
证法三:(比较法)
∵a+b=1,a>0,b>0,∴a+b≥2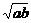 ,∴ab≤
,∴ab≤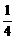
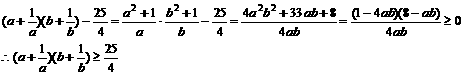
证法四:(综合法)
∵a+b=1, a>0,b>0,∴a+b≥2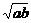 ,∴ab≤
,∴ab≤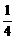 .
.
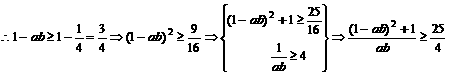
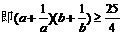
证法五:(三角代换法)
∵
a>0,b>0,a+b=1,故令a=sin2α,b=cos2α,α∈(0,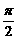 )
)
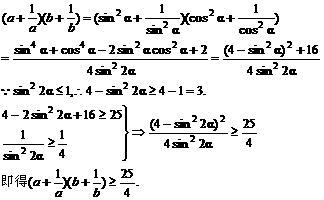 2
2
[例3]
证明不等式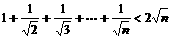 (n∈N*)
(n∈N*)
证法一:(1)当n等于1时,不等式左端等于1,右端等于2,所以不等式成立;
(2)假设n=k(k≥1)时,不等式成立,即1+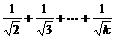 <2
<2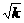 ,
,
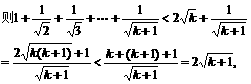
∴当n=k+1时,不等式成立.
综合(1)、(2)得:当n∈N*时,都有1+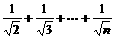 <2
<2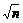 .
.
另从k到k+1时的证明还有下列证法:
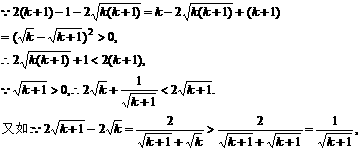
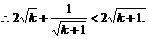
证法二:对任意k∈N*,都有:
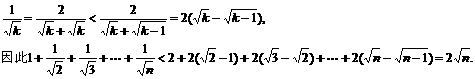
证法三:设f(n)=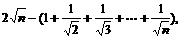
那么对任意k∈N?* 都有:
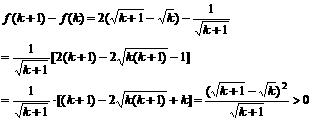
∴f(k+1)>f(k)
因此,对任意n∈N* 都有f(n)>f(n-1)>…>f(1)=1>0,
∴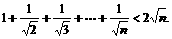
不等式的应用
[例1]

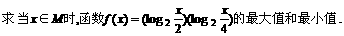
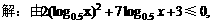
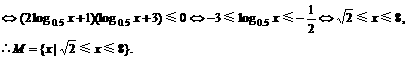

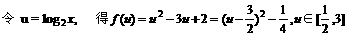
根据复合函数的单调性得:
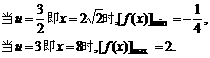
[例2]
例2、已知函数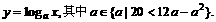
(1)判断函数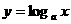 的增减性;
的增减性;
(2)若命题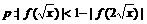 为真命题,求实数x的取值范围.
为真命题,求实数x的取值范围.
解:(1)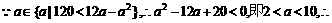 函数
函数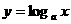 是增函数;
是增函数;
(2)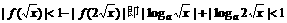 ,必有
,必有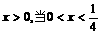 时,
时,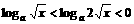 ,不等式化为
,不等式化为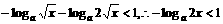 ,
,
故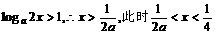 ;当
;当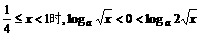 ,
,
不等式化为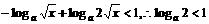 ,这显然成立,此时
,这显然成立,此时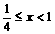 ;
;
当 时,
时,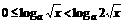 ,
,
不等式化为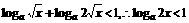
故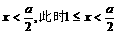 ;
;
综上所述知,使命题p为真命题的x的取值范围是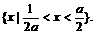
[例3]
(1994年)已知函数
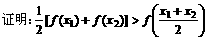
解: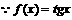
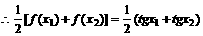
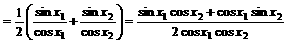
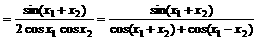
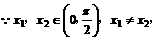
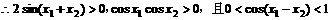
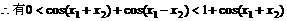
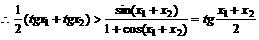
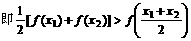
[例4]
(1995年)设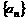 是由正数组成的等比数列,
是由正数组成的等比数列, 项之和。
项之和。
(1)证明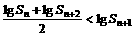
(2)是否存在常数C>0,使得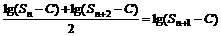 成立?并证明你的结论。
成立?并证明你的结论。
证明:(I)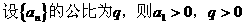
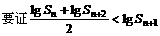
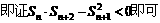
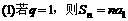
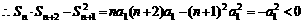
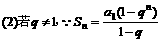
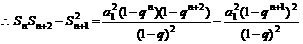
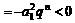
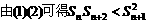
根据对数函数的单调性,可得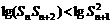
即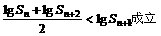
(2)不存在常数C使等式成立。
证法一:因为要使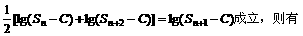
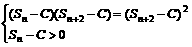
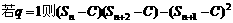
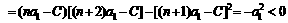

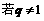
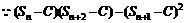
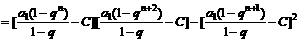

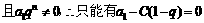
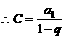 ;
;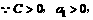
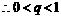

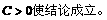
综合上面的证明可见不存在常数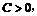
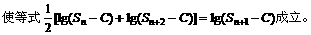
还可以直接用反证法证明:
证法二:假设存在常数C>0,使等式能够成立,则有
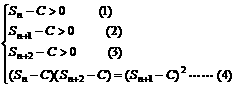
由(4)可得: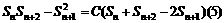
由平均值不等式可知
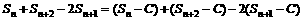
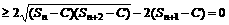
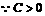
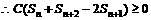
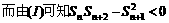
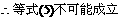
 =
=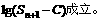
[例5]
(1990年)设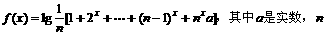 是任意给定的自然数,且
是任意给定的自然数,且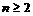 。
。
(1)如果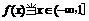 时有意义,求a的取值范围。
时有意义,求a的取值范围。
(2)如果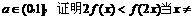 0时成立。
0时成立。
解:(I)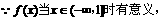
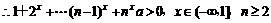 ,
,
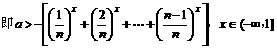
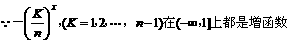
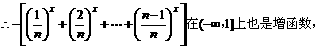
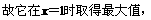
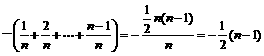
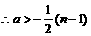 ;
;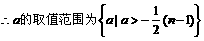
(2)证法一:
根据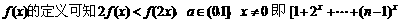
+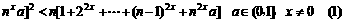
下面用数学归纳法证之。
A. 设n=2时若
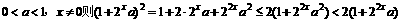 ,即(1)成立。
,即(1)成立。
若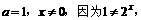
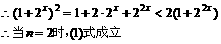
B. 设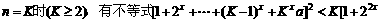
+…+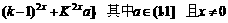
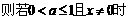
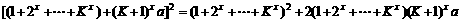
+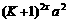
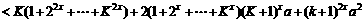
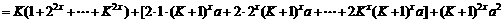
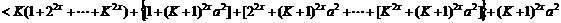
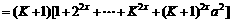
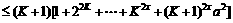
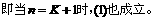

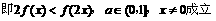
证法二:
只需证明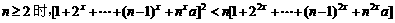 ,
,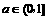 ,
,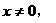
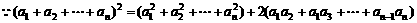
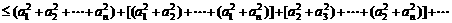
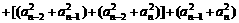
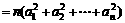
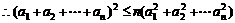
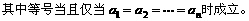
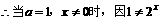
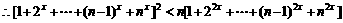
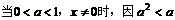
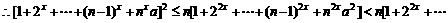
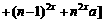
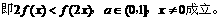
[例6]
如图,ΔABC是某屋顶的断面,CD⊥AB,横梁AB的长是竖梁CD长的2倍.设计时应使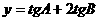 保持最小,试确定D点的位置,并求y的最小值.
保持最小,试确定D点的位置,并求y的最小值.
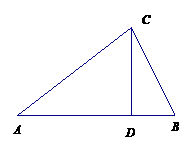 解:设AD=x,CD=1,
解:设AD=x,CD=1,
则AB=2,BD=2–x,(0<x<2)
令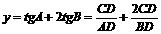

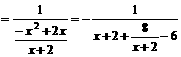
∵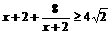 ;当且仅当
;当且仅当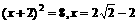 时取等号
时取等号
∴当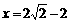 时,y取得最小值
时,y取得最小值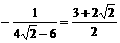
此时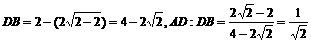
答:取AD:DB=1: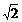 时,y有最小值
时,y有最小值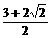
[例7]
在一容器内装有浓度为r%的溶液a升,注入浓度为p%的溶液 升,搅匀后再倒出溶液
升,搅匀后再倒出溶液 升,这叫做一次操作。
升,这叫做一次操作。
(I)设第n次操作后容器内溶液的浓度为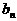 (每次注入的溶液都是p%), 计算
(每次注入的溶液都是p%), 计算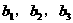 ,并归纳出
,并归纳出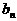 的计算公式(不要求证明)
的计算公式(不要求证明)
(II)设 要使容器内溶液浓度不小于q%,问至少要进行上述操作多少次?(已知
要使容器内溶液浓度不小于q%,问至少要进行上述操作多少次?(已知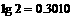 )
)
解: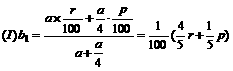

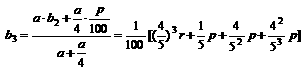
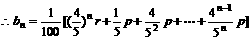
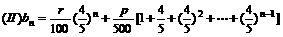
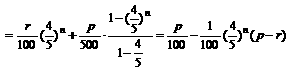
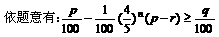
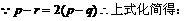
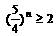
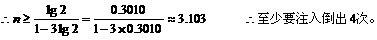
[例8]
某商场经过市场调查分析后得知,2003年从年初开始的前n个月内,对某种商品需求的累计数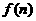 (万件)近似地满足下列关系:
(万件)近似地满足下列关系:
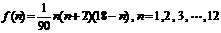
(Ⅰ)问这一年内,哪几个月需求量超过1.3万件?
(Ⅱ)若在全年销售中,将该产品都在每月初等量投放市场,为了保证该商品全年不脱销,每月初至少要投放多少件商品?(精确到件)
解:(Ⅰ)首先,第n个月的月需求量=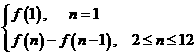
∵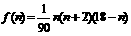 ,
,
∴ 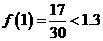 .
.
当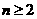 时,
时,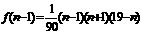
∴ 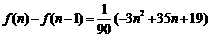
令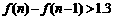 ,即
,即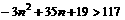 ,解得:
,解得: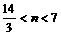 ,
,
∵ n∈N, ∴n = 5 ,6
即这一年的5、6两个月的需求量超过1.3万件.
(Ⅱ)设每月初等量投放商品a万件,要使商品不脱销,对于第n个月来说,不仅有本月投放市场的a万件商品,还有前几个月未销售完的商品.所以,需且只需: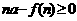 ,
,
∴ 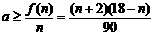
又∵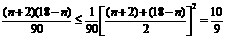 ∴
∴ 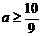
即每月初至少要投放11112件商品,才能保证全年不脱销.
[例9] 一根水平放置的长方体形枕木的安全负荷与它的宽度a成正比,与它的厚度d的平方成正比,与它的长度l的平方成反比.
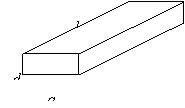 (Ⅰ)将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?
(Ⅰ)将此枕木翻转90°(即宽度变为了厚度),枕木的安全负荷变大吗?为什么?
(Ⅱ)现有一根横断面为半圆(半圆的半径为R)的木材,用它来截取成长方体形的枕木,木材长度即为枕木规定的长度,问如何截取,可使安全负荷最大?
解:(Ⅰ)由题可设安全负荷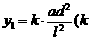 为正常数),则翻转90º后,安全负荷
为正常数),则翻转90º后,安全负荷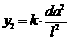 .
.
因为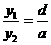 ,所以,当
,所以,当 时,
时, .安全负荷变大;
.安全负荷变大;
当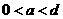 时,
时,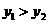 ,安全负荷变小.
,安全负荷变小.
(2)如图,设截取的枕木宽为a,高为d,则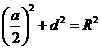 ,即
,即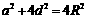 .
.
∵ 枕木长度不变,∴u=ad2最大时,安全负荷最大
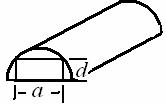 ∴
∴ 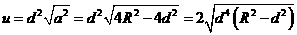
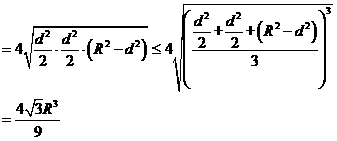
当且仅当 ,
,
即取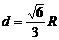 ,
,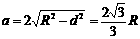 时,u最大, 即安全负荷最大.
时,u最大, 即安全负荷最大.
[例10]
现有流量均为300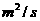 的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2
的两条河流A、B会合于某处后,不断混合,它们的含沙量分别为2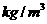 和0.2
和0.2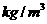 .假设从汇合处开始,沿岸设有若干个观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100
.假设从汇合处开始,沿岸设有若干个观测点,两股水流在流经相邻两个观测点的过程中,其混合效果相当于两股水流在1秒钟内交换100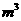 的水量,即从A股流入B股100
的水量,即从A股流入B股100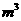 水,经混合后,又从B股流入A股100
水,经混合后,又从B股流入A股100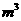 水并混合.问:从第几个观测点开始,两股河水的含沙量之差小于0.01
水并混合.问:从第几个观测点开始,两股河水的含沙量之差小于0.01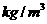 (不考虑泥沙沉淀)?
(不考虑泥沙沉淀)?
解:本题的不等关系为“两股河水的含沙量之差小于0.01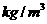 ”.但直接建构这样的不等关系较为困难.为表达方便,我们分别用
”.但直接建构这样的不等关系较为困难.为表达方便,我们分别用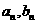 来表示河水在流经第n个观测点时,A水流和B水流的含沙量.
来表示河水在流经第n个观测点时,A水流和B水流的含沙量.
则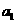 =2
=2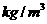 ,
,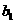 =0.2
=0.2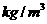 ,且
,且
 .(*)
.(*)
由于题目中的问题是针对两股河水的含沙量之差,所以,我们不妨直接考虑数列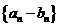 .
.
由(*)可得:
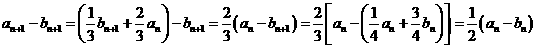
所以,数列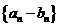 是以
是以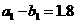 为首项,以
为首项,以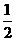 为公比的等比数列.
为公比的等比数列.
所以,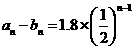 .
.
由题,令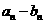 < 0.01,得
< 0.01,得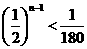 .所以,
.所以,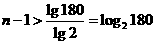 .
.
由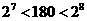 得
得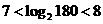 ,所以,
,所以,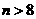 .
.
即从第9个观测点开始,两股水流的含沙量之差小于0.01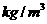 .
.
[例11]
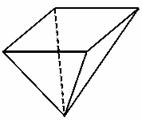 用一块钢锭烧铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器(如右图)设容器高为h米,盖子边长为a米,
用一块钢锭烧铸一个厚度均匀,且表面积为2平方米的正四棱锥形有盖容器(如右图)设容器高为h米,盖子边长为a米,
(1)求a关于h的解析式;
(2)设容器的容积为V立方米,则当h为何值时,V最大?求出V的最大值(求解本题时,不计容器厚度)
解:①设h′是正四棱锥的斜高,由题设可得:
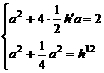 消去
消去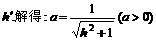
②由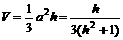 (h>0)
(h>0)
得: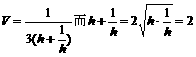
所以V≤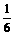 ,当且仅当h=
,当且仅当h=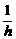 即h=1时取等号
即h=1时取等号
故当h=1米时,V有最大值,V的最大值为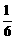 立方米.
立方米.
7.强化不等式的应用高考中除单独考查不等式的试题外,常在一些函数、数列、立体几何、解析几何和实际应用问题的试题中涉及不等式的知识,加强不等式应用能力,是提高解综合题能力的关键.因此,在复习时应加强这方面训练,提高应用意识,总结不等式的应用规律,才能提高解决问题的能力. 如在实际问题应用中,主要有构造不等式求解或构造函数求函数的最值等方法,求最值时要注意等号成立的条件,避免不必要的错误.
6.重视数学思想方法的复习根据本章上述的命题趋向我们迎考复习时应加强数学思想方法的复习.在复习不等式的解法时,加强等价转化思想的训练与复习.解不等式的过程是一个等价转化的过程,通过等价转化可简化不等式(组),以快速、准确求解.加强分类讨论思想的复习.在解不等式或证不等式的过程中,如含参数等问题,一般要对参数进行分类讨论.复习时,学生要学会分析引起分类讨论的原因,合理的分类,做到不重不漏.加强函数与方程思想在不等式中的应用训练.不等式、函数、方程三者密不可分,相互联系、互相转化.如求参数的取值范围问题,函数与方程思想是解决这类问题的重要方法.在不等式的证明中,加强化归思想的复习,证不等式的过程是一个把已知条件向要证结论的一个转化过程,既可考查学生的基础知识,又可考查学生分析问题和解决问题的能力,正因为证不等式是高考考查学生代数推理能力的重要素材,复习时应引起我们的足够重视.利用函数f(x)=x+ (a>0)的单调性解决有关最值问题是近几年高考中的热点,应加强这方面的训练和指导.
4.熟练掌握利用平均值不等式求最值的方法及其使用条件,并重视在几何和实际问题中的应用。
5,通过训练,使学生掌握等价转化思想和化归思想,培养学生的代数推理能力,提高学生应用不等式知识解决问题的能力.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com