
题目列表(包括答案和解析)
3.设函数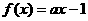 ,且
,且 的图象过点
的图象过点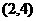 ,则
,则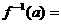
A.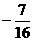 B.
B.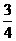 C.
C.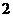 D.
D.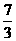
2.已知数列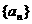 为等差数列,且
为等差数列,且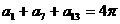 ,则
,则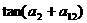
A. B.
B.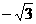 C.
C.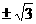 D.
D.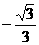
1.已知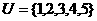 ,
,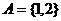 ,
,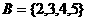 ,则
,则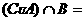
A.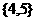 B.
B.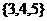 C.
C.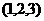 D.
D.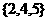
22. 已知函数
(1)若函数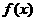 存在单调递减区间,求
存在单调递减区间,求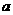 的取值范围;
的取值范围;
(2)若 且关于x的方程
且关于x的方程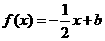 在
在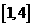 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数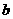 的取值范围;
的取值范围;
(3)设各项为正的数列 满足:
满足: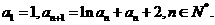 求证:
求证: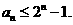
21. 标准椭圆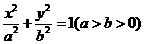 的两焦点为
的两焦点为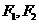 ,
,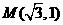 在椭圆上,且
在椭圆上,且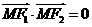 .
.
(1)求椭圆方程;
(2)若N在椭圆上,O为原点,直线 的方向向量为
的方向向量为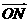 ,若
,若 交椭圆于A、B两点,且NA、NB与
交椭圆于A、B两点,且NA、NB与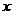 轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
轴围成的三角形是等腰三角形(两腰所在的直线是NA、NB),则称N点为椭圆的特征点,求该椭圆的特征点.
20. 已知等差数列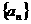 满足:
满足: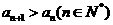 ,
,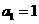 ,该数列的前三项分别加上1,1,3后顺次成为等比数列
,该数列的前三项分别加上1,1,3后顺次成为等比数列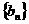 的前三项.
的前三项.
(1)分别求数列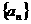 ,
,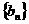 的通项公式
的通项公式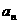 ,
, ;
;
(2)设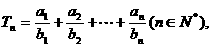 若
若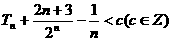 恒成立,求c的最小值.
恒成立,求c的最小值.
19. 如图:在各棱长均为2的三棱柱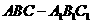 中,
中, ,侧面
,侧面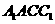
 底面
底面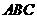 ,
,
(1)求棱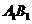 与平面
与平面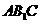 所成的角的大小;
所成的角的大小;
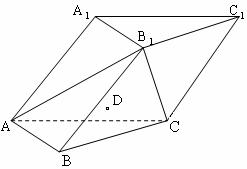 (2)已知D点满足
(2)已知D点满足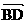 =
=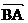 +
+ ,在直线
,在直线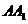 上是否
上是否
存在点P,使DP∥平面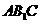 ?若存在,确定P点的
?若存在,确定P点的
位置,若不存在,请说明理由.
18. 美国次贷危机引发2008年全球金融动荡,波及中国股市,甲、乙、丙、丁四人打算趁目前股市低迷之际“抄底”,.若四人商定在圈定的6只股票中各自随机购买一只(假定购买时每支股票的基本情况完全相同).
(1)求甲、乙、丙、丁四人恰好买到同一只股票的概率;
(2)求甲、乙、丙、丁四人中至多有两人买到同一只股票的概率;
(3)(只理科做)由于国家采取了积极的救市措施,股市渐趋“回暖”.若某人今天按上一交易日的收盘价20元/股,买入某只股票1000股,且预计今天收盘时,该只股票比上一交易日的收盘价上涨10%(涨停)的概率为0.6.持平的概率为0.2,否则将下跌10%(跌停),求此人今天获利的数学期望(不考虑佣金、印花税等交易费用).
17. 已知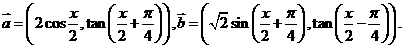 令
令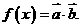
(1)求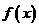 的单调增区间;
的单调增区间;
(2)若 时,
时,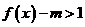 恒成立,求
恒成立,求 的取值范围.
的取值范围.
16. 对一切实数,令 为不大于
为不大于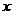 的最大整数,则函数
的最大整数,则函数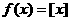 称为高斯函数或取整函数.若
称为高斯函数或取整函数.若
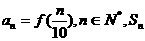 为数列
为数列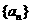 的前
的前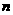 项和,则
项和,则 = .
= .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com