
题目列表(包括答案和解析)
19. 解:(1)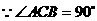 即
即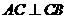
又平面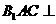 平面
平面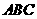
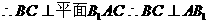 ………………4分
………………4分
(2)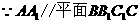
∴点 到平面
到平面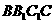 的距离即求点
的距离即求点 到平面
到平面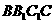 的距离
的距离
取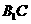 中点
中点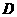 ,连结
,连结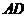
∵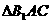 为等边三角形
为等边三角形
 ∴
∴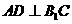
又由(1)知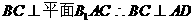
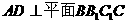
又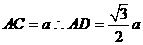
∴点 到平面
到平面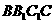 的距离即点
的距离即点 到平面
到平面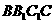 的距离为
的距离为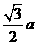 ………………8分
………………8分
(3)二面角 即二面角
即二面角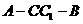
过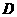 作
作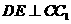 ,垂足为点
,垂足为点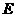 ,连结
,连结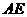
由(2)及三垂线定理知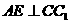
∴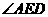 为二面角
为二面角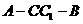 的平面角
的平面角
由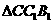 ∽
∽ 得
得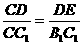
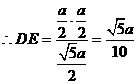
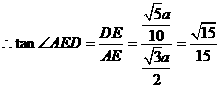
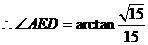 …12分
…12分
解法2:(1)如图,取 中点
中点 ,连结
,连结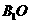
∵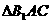 为等边三角形
为等边三角形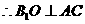
又∵平面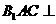 平面
平面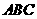
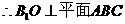
建立空间直角坐标系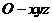 ,则有
,则有
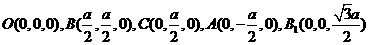
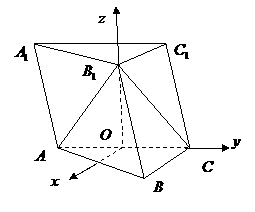
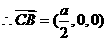 ,
,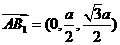
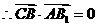 即
即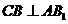 ………………4分
………………4分
(2)设平面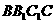 的一个法向量为
的一个法向量为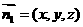
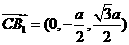
由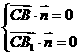 得
得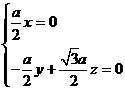 令
令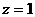 得
得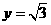
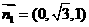
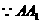 ∥
∥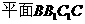 ∴点
∴点 到平面
到平面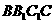 的距离即求点
的距离即求点 到平面
到平面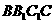 的距离
的距离
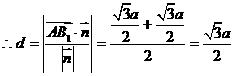 ………………………………8分
………………………………8分
(3)平面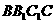 的一个法向量为
的一个法向量为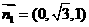
设平面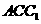 的一个法向量为
的一个法向量为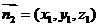
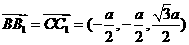 ,
,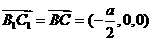
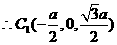
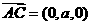
由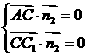 得
得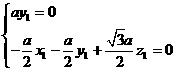 令
令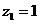 得
得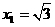
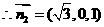
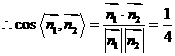
∴二面角 的大小为
的大小为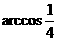 …………………………………12分
…………………………………12分
18. 解:(1)恰有两门学科被选择的概率为
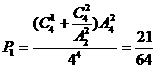 ………………………………6分
………………………………6分
(2)至少有两人被录取的概率为
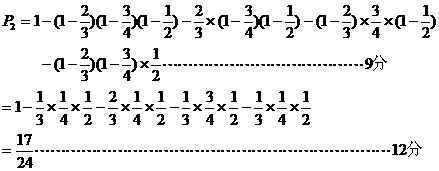
17. (1)由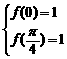 得:
得: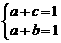 , ……………………………… 2分
, ……………………………… 2分
即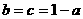 ,
,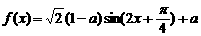 ……………… 4分
……………… 4分
当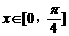 时,
时,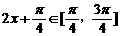 ,
,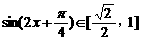
因为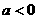 ,有
,有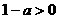 ,
,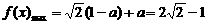 ,得
,得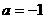
故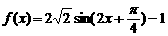 …………………………… 8分
…………………………… 8分
(2)∵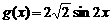 是奇函数,且将
是奇函数,且将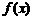 的图象先向右平移
的图象先向右平移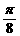 个单位,再向上平移1个单位,可以得到
个单位,再向上平移1个单位,可以得到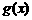 的图象,∴
的图象,∴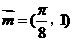 是满足条件的一个平移向量.……12分
是满足条件的一个平移向量.……12分
13. 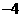 14.
14. 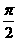 15.
15.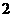 16. ①②③
16. ①②③
22.(本小题满分14分)已知函数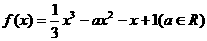
(1)若函数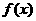 在
在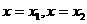 处取得极值,且
处取得极值,且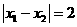 ,求
,求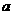 的值及
的值及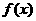 的单调区间;
的单调区间;
(2)若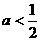 ,讨论曲线
,讨论曲线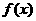 与
与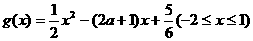 的交点个数.
的交点个数.
 年江西省八校联合考试数学(文)
年江西省八校联合考试数学(文)
21.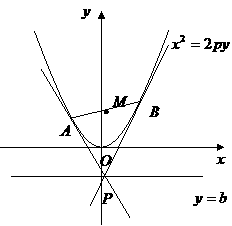 (本小题满分12分)如图,已知抛物线
(本小题满分12分)如图,已知抛物线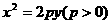 和直线
和直线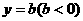 ,点
,点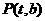 在直线
在直线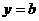 上移动,过点
上移动,过点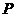 作抛物线的两条切线,切点分别为
作抛物线的两条切线,切点分别为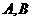 ,线段
,线段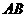 的中点为
的中点为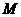 .
.
(1)求点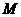 的轨迹;
的轨迹;
(2)求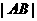 的最小值;
的最小值;
20.(本小题满分12分)已知各项均为正数的数列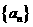 的前
的前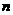 项和为
项和为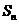 ,且
,且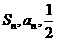 成等差数列.
成等差数列.
(1)求数列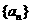 的通项公式; (2)若
的通项公式; (2)若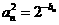 ,设
,设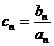 求数列
求数列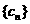 的前项和
的前项和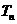 .
.
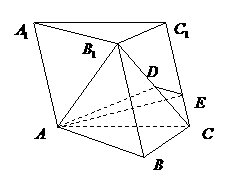
19.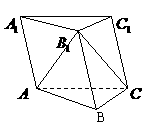 (本小题满分12分)如图,在斜三棱柱
(本小题满分12分)如图,在斜三棱柱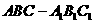 中,平面
中,平面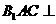 平面
平面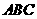 ,
, 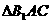 为等边三角形,
为等边三角形,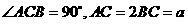 .
.
(1)求证: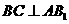 ;
;
(2)求点 到平面
到平面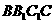 的距离;
的距离;
(3)求二面角 的大小.
的大小.
18.(本小题满分12分)某校奥赛辅导班报名正在进行,甲、乙、丙、丁四名学生跃跃欲试,现有四门学科(数学、物理、化学、信息技术)可供选择,每位学生只能任选其中一科.
(1)求恰有两门学科被选择的概率;
(2)已知报名后,丁已指定被录取.另外,甲被录取的概率为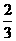 ,乙被录取的概率为
,乙被录取的概率为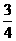 ,丙被录取的概率为
,丙被录取的概率为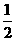 ,求甲、乙、丙三人中至少有两人被录取的概率.
,求甲、乙、丙三人中至少有两人被录取的概率.
17.(本题满分12分)已知函数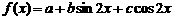
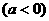 的图象经过点
的图象经过点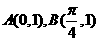 ,且当
,且当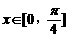 时,
时,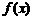 的最大值为
的最大值为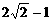 .
.
(1)求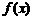 的解析式;
的解析式;
(2)是否存在向量 ,使得将
,使得将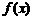 的图象按照向量
的图象按照向量 平移后可以得到一个奇函数的图象?若存在,请求出满足条件的一个
平移后可以得到一个奇函数的图象?若存在,请求出满足条件的一个 ;若不存在,请说明理由.
;若不存在,请说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com