
题目列表(包括答案和解析)
13、在下列关于直线l、m与平面α、β的命题中,真命题是 ( )
(A)若l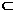 β,且α⊥β,则l⊥α. (B)若l⊥β,且α∥β,则l⊥α.
β,且α⊥β,则l⊥α. (B)若l⊥β,且α∥β,则l⊥α.
(C)若α∩β=m,且l∥m,则l∥α (D)若l⊥β,且α⊥β,则l∥α.
20. 已知函数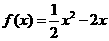 ,
,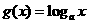 。如果函数
。如果函数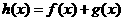 没有极值点,且
没有极值点,且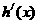 存在零点。(1)求
存在零点。(1)求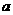 的值;(2)判断方程
的值;(2)判断方程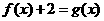 根的个数并说明理由;(3)设点
根的个数并说明理由;(3)设点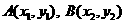
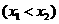 是函数
是函数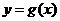 图象上的两点,平行于AB 的切线以
图象上的两点,平行于AB 的切线以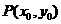 为切点,求证:
为切点,求证: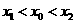 。
。
19. 在直角坐标平面上有一点列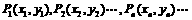 ,对一切正整数n,点
,对一切正整数n,点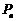 位于函数
位于函数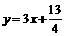 的图象上,且
的图象上,且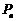 的横坐标构成以
的横坐标构成以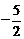 为首项,
为首项,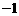 为公差的等差数列
为公差的等差数列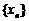 .
.
⑴求点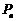 的坐标;⑵设抛物线列
的坐标;⑵设抛物线列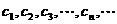 中的每一条的对称轴都垂直于
中的每一条的对称轴都垂直于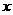 轴,第
轴,第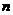 条抛物线
条抛物线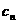 的顶点为
的顶点为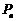 ,且过点
,且过点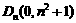 ,设与抛物线
,设与抛物线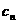 相切于
相切于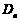 的直线斜率为
的直线斜率为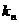 ,求:
,求: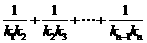 ;⑶设
;⑶设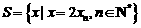 ,
,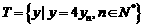 ,等差数列{
,等差数列{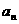 }的任一项
}的任一项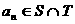 ,其中
,其中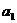 是
是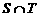 中的最大数,
中的最大数,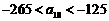 ,求{
,求{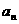 }的通项公式。
}的通项公式。
18.已知圆A: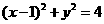 与
与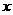 轴负半轴交于B点,过B的弦BE与
轴负半轴交于B点,过B的弦BE与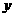 轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆。(1)求椭圆的方程;(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值。
轴正半轴交于D点,且2BD=DE,曲线C是以A,B为焦点且过D点的椭圆。(1)求椭圆的方程;(2)点P在椭圆C上运动,点Q在圆A上运动,求PQ+PD的最大值。
17.已知向量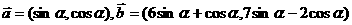 ,设函数
,设函数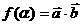 .
.
(Ⅰ)求函数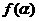 的最大值;
的最大值;
(Ⅱ)在锐角三角形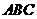 中,角
中,角 、
、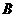 、
、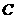 的对边分别为
的对边分别为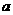 、
、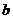 、
、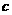 ,
,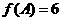 , 且
, 且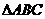 的面积为
的面积为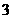 ,
,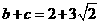
 ,求
,求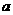 的值.
的值.
16. 在直三棱柱ABC-A1B1C1中,AB1⊥BC1,AB=CC1=a,BC=b.
(1)设E、F分别为AB1、BC1的中点,求证:EF∥平面ABC;(2)求证:AC⊥AB;(3)求四面体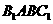 的体积.
的体积.
15.已知关于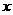 的一元二次方程
的一元二次方程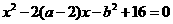 .
.
(Ⅰ)若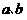 是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
是一枚骰子掷两次所得到的点数,求方程有两正根的概率;
(Ⅱ)若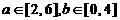 ,求方程没有实根的概率.
,求方程没有实根的概率.
14.下列说法:①当 ;②
;②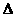 ABC中,
ABC中,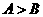 是
是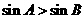 成立的充要条件;③函数
成立的充要条件;③函数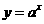 的图象可以由函数
的图象可以由函数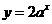 (其中
(其中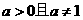 )平移得到;④已知
)平移得到;④已知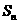 是等差数列
是等差数列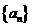 的前
的前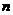 项和,若
项和,若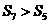 ,则
,则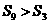 .;⑤函数
.;⑤函数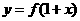 与函数
与函数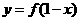 的图象关于直线
的图象关于直线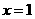 对称。其中正确的命题的序号为 ▲
对称。其中正确的命题的序号为 ▲
13.若函数式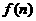 表示
表示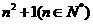 的各位上的数字之和,如
的各位上的数字之和,如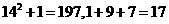 ,所以
,所以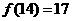 ,记
,记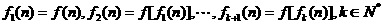 ,则
,则
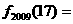 ▲
▲
12.已知点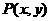 满足
满足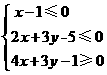 ,点
,点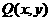 在圆
在圆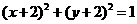 上,则
上,则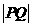 的最大值与最小值为
▲
的最大值与最小值为
▲
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com