
题目列表(包括答案和解析)
2.设集合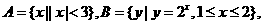 则
则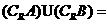 ( )
( )
A.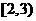 B.
B.
 C.
C. D.
D.
1.复数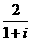 的模的值为( )
的模的值为( )
A.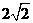 B.2 C.
B.2 C.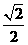 D.
D.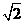
(17)(本小题满分10分)
已知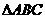 的内角
的内角 、
、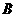 、
、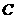 所对的边分别为
所对的边分别为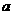 、
、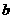 、
、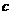 ,向量
,向量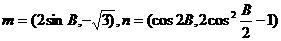 ,且
,且 ∥
∥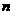 ,
,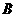 为锐角.
为锐角.
(Ⅰ)求角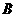 的大小;
的大小;
(Ⅱ)如果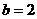 ,求
,求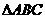 的面积
的面积 的最大值.
的最大值.
(18)(本小题满分12分)
某车间在两天内,每天生产10件某产品,其中第一天、第二天分别生产出了1件、2件次品.而质检部门每天要从生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(Ⅰ)求第一天产品通过检查的概率;
(Ⅱ)若厂内对车间生产的产品采用记分制:两天全不通过检查得0分;通过1天、2天分别得1分、2分.求该车间这两天的所得分 的数学期望.
的数学期望.
(19)(本小题满分12分)
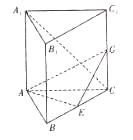 如图,在直三棱柱
如图,在直三棱柱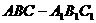 中,
中,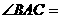 90°,
90°,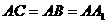 ,
,
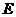 是
是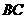 的中点.
的中点.
(Ⅰ)求异面直线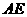 与
与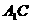 所成的角;
所成的角;
(Ⅱ)若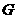 为
为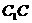 上一点,且
上一点,且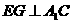 ,求二面角
,求二面角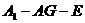 的大小.
的大小.
(20)(本小题满分12分)
已知函数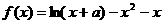 在
在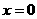 处取得极值.
处取得极值.
(Ⅰ)求实数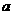 的值;
的值;
(Ⅱ)若关于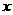 的方程
的方程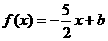 在区间
在区间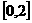 上恰有两个不同的实数根,求实
上恰有两个不同的实数根,求实
数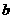 的取值范围.
的取值范围.
(21)(本小题满分12分)
已知点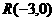 ,点
,点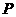 在
在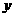 轴上,点
轴上,点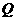 在
在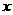 轴的正半轴上,点
轴的正半轴上,点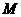 在直线
在直线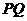 上,且
上,且
满足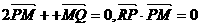 .
.
(Ⅰ)当点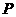 在
在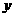 轴上移动时,求点
轴上移动时,求点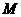 的轨迹
的轨迹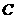 的方程;
的方程;
(Ⅱ)设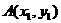 、
、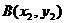 为轨迹
为轨迹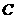 上两点,且
上两点,且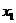 >1,
>1, 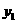 >0,
>0,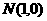 ,求实数
,求实数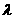 ,
,
使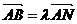 ,且
,且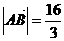 .
.
(22)(本小题满分12分)
设数列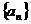 、
、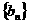 满足
满足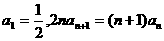 ,且
,且
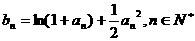 .
.
(Ⅰ)求数列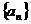 的通项公式;
的通项公式;
(Ⅱ)对一切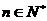 ,证明
,证明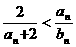 成立;
成立;
(Ⅲ)记数列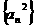 、
、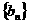 的前
的前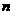 项和分别是
项和分别是 、
、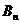 ,证明:
,证明: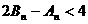 .
.
2009年高考桂林市、崇左市、贺州市、防城港市联合调研考试
(13)以点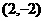 为圆心并且与圆
为圆心并且与圆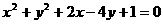 相外切的圆的方程是 .
相外切的圆的方程是 .
(14)已知等差数列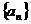 的前20项的和为100,那么
的前20项的和为100,那么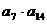 的最大值为
.
的最大值为
.
(15)设 为坐标原点,点
为坐标原点,点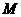 坐标为
坐标为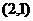 ,若
,若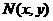 满足不等式组:
满足不等式组: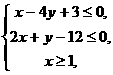 则
则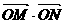 的最大值为
.
的最大值为
.
(16)过双曲线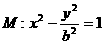 的左顶点
的左顶点 作斜率为
作斜率为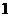 的直线
的直线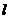 ,若
,若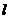 与双曲线
与双曲线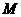 的两条渐近线相交与
的两条渐近线相交与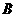 、
、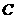 两点,且
两点,且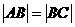 ,则双曲线
,则双曲线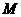 的离心率为
.
的离心率为
.
(1) 已知集合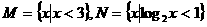 ,则
,则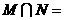
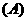
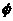 .
. 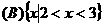 .
. 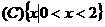 .
. 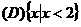 .
.
(2) 设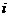 为虚数单位,则
为虚数单位,则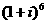 展开式中的第三项为
展开式中的第三项为
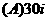 .
. 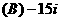 .
.
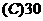 .
.
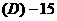 .
.
(3) 已知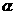 、
、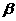 是不同的平面,
是不同的平面, 、
、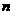 是不同的直线,则下列命题不正确的是
是不同的直线,则下列命题不正确的是
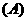 若
若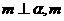 ∥
∥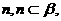 则
则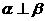 .
. 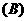 若
若 ∥
∥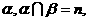 则
则 ∥
∥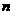
 若
若 ∥
∥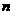 ,
,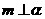 ,则
,则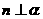 .
.
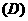 若
若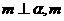
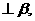 则
则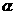 ∥
∥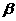 .
.
(4) 下列函数中,在区间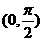 上为增函数且以
上为增函数且以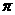 为周期的函数是
为周期的函数是
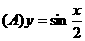 .
. 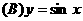 .
. 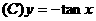 .
. 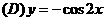 .
.
(5) 若抛物线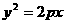 的焦点与椭圆
的焦点与椭圆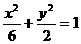 的右焦点重合,则
的右焦点重合,则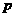 的值为
的值为
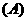 2.
2.
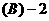 .
.
 4.
4. 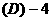 .
.
(6) 函数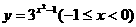 的反函数是
的反函数是
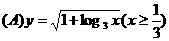 .
.
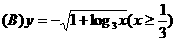 .
.
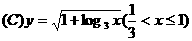 .
. 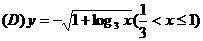 .
.
(7) 对于函数:①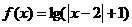 ;②
;②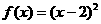 ;③
;③ .有如下三个命题:
.有如下三个命题:
命题甲: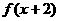 是偶函数;
是偶函数;
命题乙: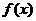 在
在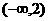 上是减函数,在
上是减函数,在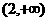 上是增函数;
上是增函数;
命题丙: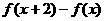 在
在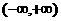 上是增函数.
上是增函数.
能使命题甲、乙、丙均为真的所有函数的序号是
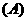 ①③.
①③.
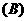 ①②.
①②.
 ③.
③.
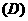 ②.
②.
(8) 有七名同学站成一排找毕业纪念照,其中甲必须站在正中间,并且乙、丙两位同学要站在一起,则不同的站法有
 240种.
240种.
 192种.
192种.  96种.
96种.  48种.
48种.
(9) 设函数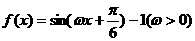 的导数
的导数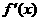 最大值为3,则
最大值为3,则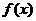 的图像的一条对称轴的方程是
的图像的一条对称轴的方程是
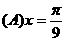 .
.
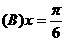 .
.
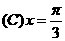 .
. 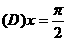 .
.
(10) 已知向量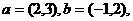 若
若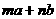 与
与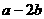 共线,则
共线,则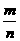 等于
等于
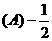 .
.
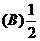 .
.
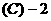 .
.
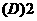 .
.
(11) 若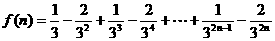 (其中
(其中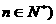 ,则
,则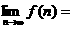
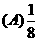 .
.
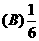 .
.
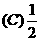 .
.
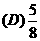 .
.
(12) 从点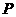 出发的三条射线
出发的三条射线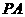 、
、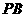 、
、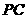 两两成60°角,且分别与球
两两成60°角,且分别与球 相切于
相切于 、
、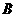 、
、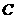 三点.若球的体积为
三点.若球的体积为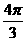 ,则
,则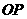 的长度为
的长度为
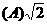 .
.
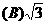 .
.
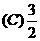 .
.
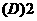 .
.
第Ⅱ卷
22.已知数列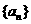 满足
满足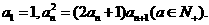
(I)求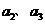 及
及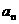 ;
;
(Ⅱ)设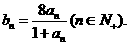 求证
求证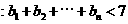
21.已知椭圆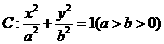 过点
过点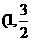 ),且离心率
),且离心率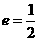 .
.
(I)求椭圆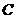 的方程;
的方程;
(Ⅱ)设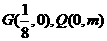 若椭圆
若椭圆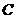 上存在横坐标不同的两点
上存在横坐标不同的两点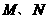 ,使
,使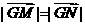 ,且
,且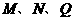 共线,求实数
共线,求实数 的取值范围。
的取值范围。
20.已知函数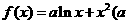 为实常数).
为实常数).
(I)求函数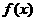 在区间
在区间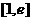 上的最小值及相应的
上的最小值及相应的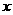 值;
值;
(Ⅱ)若存在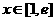 ,使得
,使得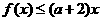 成立,求实数
成立,求实数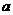 的取值范围。
的取值范围。
19.美国次贷危机引发2008年全球金融动荡,波及中国两大股市.甲、乙、丙三人打算趁股市低迷之际投资股市,三人商定在圈定的10支股票中各自独立随即购买一支。
(I)求甲、乙、丙三人中至少有两人买到同一支股票的概率;
(Ⅱ)由于国家采取了积极的救市措施,股市渐趋回暖,若甲今天按上交易日的收盘价20远/股买入1000股,且雨季今天收盘时,该股涨停(比上一交易日的收盘价上涨10%)的概率为0.5,持平的概率为0.2,否则将下跌5%,求甲今天获利的数学期望(不考虑交易税)。
18.如图,在矩形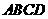 中,
中,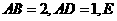 是
是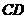 的中点,以
的中点,以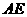 为折痕将
为折痕将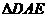 向
向
上折起。使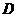 为
为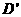 ,且平面
,且平面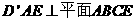
(I)求证: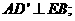
(Ⅱ)求直线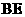 与平面
与平面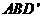 所成角的大小。
所成角的大小。

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com