
题目列表(包括答案和解析)
2. 辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,时速在
辆汽车通过某一段公路时的时速的频率分布直方图如右图所示,时速在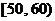 的汽车大约有
的汽车大约有
A.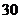 辆
B.
辆
B. 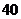 辆 C.
辆 C.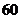 辆 D.80辆
辆 D.80辆
1. 在复平面内,复数
在复平面内,复数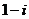 对应的点与原点的距离是
对应的点与原点的距离是
A. l
B.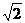 C.2
D.2
C.2
D.2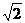
21. (本题满分14分)
解:(Ⅰ)点C的轨迹方程为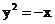 ,.............................4'
,.............................4'
(Ⅱ).由方程组
|
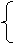 y2=-x,
y2=-x,
y=k(x+1)
ky2+y-k=0.
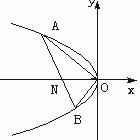 设A(x1,y1)、B(x2,y2),由韦达定理
设A(x1,y1)、B(x2,y2),由韦达定理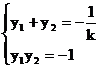 .............6'
.............6'
∵A、B在抛物线y2=-x上,
∴y12=-x1,y22=-x2,y12·y22=x1x2.
设直线l与x轴交于点N,则N(-1,0)
∵S△OAB=S△OAN+S△OBN
=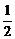 |ON||y1|+
|ON||y1|+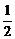 |ON||y2|
|ON||y2|
=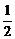 |ON|·|y1-y2|,
|ON|·|y1-y2|,
∴S△OAB=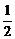 ·1·
·1·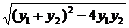
=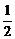
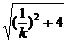 .............................................8'
.............................................8'
∵S△OAB=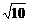 ,
,
∴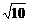 =
=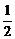
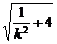 .解得k=±
.解得k=±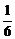 ...................................10'
...................................10'
(Ⅲ)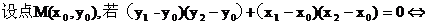
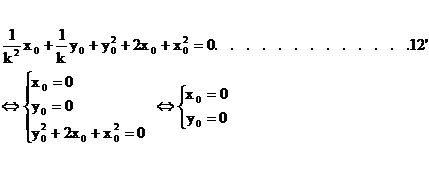
故存在唯一的合乎题意的点M(0,0).............................14'
20.(本小题满分13分)
解:(Ⅰ) 由f(x)为奇函数知b=d=0.......................2'
又f’(-1)=0且f(-1)=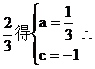 f(x)=
f(x)=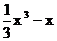 ..........4'
..........4'
(Ⅱ)由(Ⅰ)知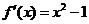
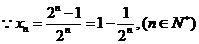 ,
,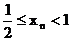 .. .........6'
.. .........6'
因为当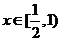 时,
时,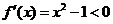 ,即函数
,即函数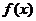 在
在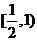 上递减
上递减
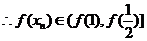 ,即
,即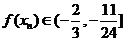 ..............8'
..............8'
又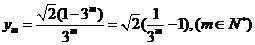 ,
,
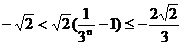 ................................10'
................................10'
又因为当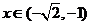 时,
时,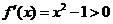 ,即函数
,即函数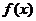 在
在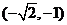 上递增;
上递增;
当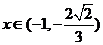 时,
时,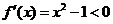 ,即函数
,即函数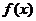 在
在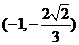 上递减
上递减
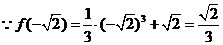 ,
,
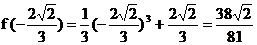
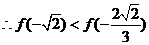 ,
,
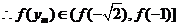 ,
,
即: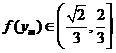 ............................................12'
............................................12'
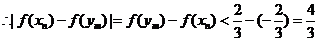 ....................13'
....................13'
19.(本小题满分12分)

(Ⅱ)由题设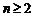 时,
时,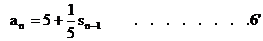

由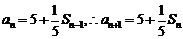 ,两式相减得:
,两式相减得:
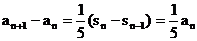
 ,
,
又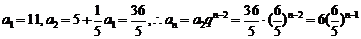 ,
,
由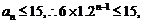
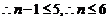 ..............................................10'
..............................................10'
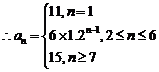 ...........................................12'
...........................................12'
18.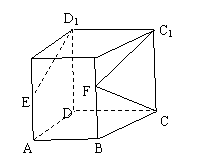 (本小题满分12分)
(本小题满分12分)
|

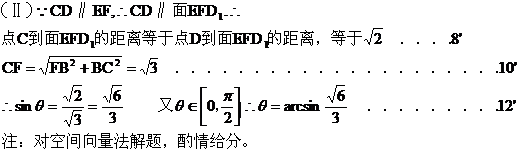
17.(本小题满分12分)
解:记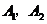 分别表示甲取得良好、优秀,
分别表示甲取得良好、优秀,
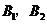 分别表示乙取得合格、良好,
分别表示乙取得合格、良好,
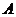 表示在一轮竞赛中,甲取得的成绩优于乙取得的成绩
表示在一轮竞赛中,甲取得的成绩优于乙取得的成绩
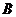 表示在三轮竞赛中至少有两轮甲取得的成绩优于乙取得的成绩,
表示在三轮竞赛中至少有两轮甲取得的成绩优于乙取得的成绩,
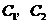 分别表示三轮中恰有两轮,三轮甲取得的成绩优于乙取得的成绩.则
分别表示三轮中恰有两轮,三轮甲取得的成绩优于乙取得的成绩.则
(Ⅰ)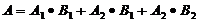 ,···················· 2分
,···················· 2分
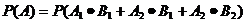
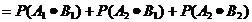
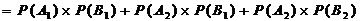
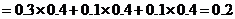 .···················· 6分
.···················· 6分
(Ⅱ)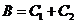 ,···························· 8分
,···························· 8分
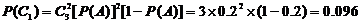 ,
,
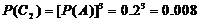 ,
,
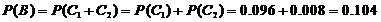 .········· 12分
.········· 12分
13. 2;
14. 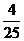 ;
15. 55,220.
;
15. 55,220.
11.
4,
12. 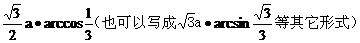
 ;
;
21.(本题满分14分)
已知动圆C过定点F(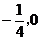 ),且与直线x=
),且与直线x=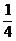 相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)
相切,圆心C的轨迹记为E.,曲线E与直线l:y=k(x+1)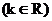 相交于A、B两点.
相交于A、B两点.
(Ⅰ)求曲线E的方程;
(Ⅱ)当△OAB的面积等于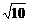 时,求k的值;
时,求k的值;
(Ⅲ)在曲线E上,是否存在与k的取值无关的定点M,使得MA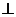 MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由.
MB?若存在,求出所有符合条件的定点M;若不存在,请说明理由.
文科数学评分细则
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com