
题目列表(包括答案和解析)
1.若向量a=(1,1),b=(-1,1),c=(4,2),则c=
A.3a+b
B. 3a-b
C.-a+3b
D. a+3b
(17)(本小题满分10分)
等比数列{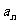 }的前n 项和为
}的前n 项和为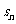 ,已知
,已知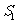 ,
,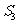 ,
,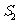 成等差数列
成等差数列
(1)求{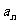 }的公比q;
}的公比q;
(2)求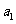 -
-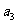 =3,求
=3,求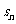
(18)(本小题满分12分)
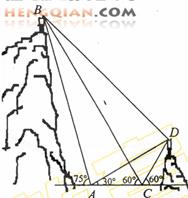
如图,A,B,C,D都在同一个与水平面垂直的平面内,B,D为两岛上的两座灯塔的塔顶。测量船于水面A处测得B点和D点的仰角分别为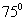 ,
,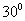 ,于水面C处测得B点和D点的仰角均为
,于水面C处测得B点和D点的仰角均为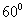 ,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,
,AC=0.1km。试探究图中B,D间距离与另外哪两点距离相等,然后求B,D的距离(计算结果精确到0.01km,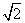
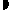 1.414,
1.414,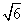
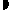 2.449)
2.449)
(19)(本小题满分12分)
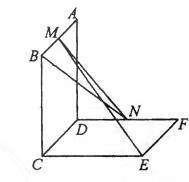
如图,已知两个正方形ABCD 和DCEF不在同一平面内,M,N分别为AB,DF的中点。
(I)若CD=2,平面ABCD ⊥平面DCEF,求直线MN的长;
(II)用反证法证明:直线ME 与 BN 是两条异面直线。
(20)(本小题满分12分)
某企业有两个分厂生产某种零件,按规定内径尺寸(单位:mm)的值落在(29.94,30.06)的零件为优质品。从两个分厂生产的零件中个抽出500件,量其内径尺寸,的结果如下表:
甲厂
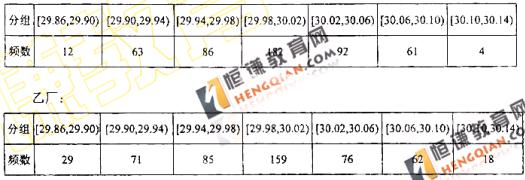
(1) 试分别估计两个分厂生产的零件的优质品率;
(2)
由于以上统计数据填下面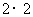 列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
列联表,并问是否有99%的把握认为“两个分厂生产的零件的质量有差异”。
|
|
甲 厂 |
乙 厂 |
合计 |
|
优质品 |
|
|
|
|
非优质品 |
|
|
|
|
合计 |
|
|
|
附: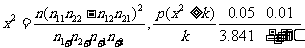
(21)(本小题满分12分)
设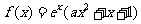 ,且曲线y=f(x)在x=1处的切线与x轴平行。
,且曲线y=f(x)在x=1处的切线与x轴平行。
(I) 求a的值,并讨论f(x)的单调性;
(II)
证明:当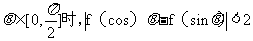
(22)(本小题满分12分)
已知,椭圆C以过点A(1,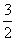 ),两个焦点为(-1,0)(1,0)。
),两个焦点为(-1,0)(1,0)。
(1) 求椭圆C的方程;
(2) E,F是椭圆C上的两个动点,如果直线AE的斜率与AF的斜率互为相反数,证明直线EF的斜率为定值,并求出这个定值。
(1)已知集合M=﹛x|-3<x 5﹜,N=﹛x|x<-5或x>5﹜,则M
5﹜,N=﹛x|x<-5或x>5﹜,则M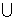 N=
N=
(A) ﹛x|x<-5或x>-3﹜ (B) ﹛x|-5<x<5﹜
(C) ﹛x|-3<x<5﹜ (D) ﹛x|x<-3或x>5﹜
(2)已知复数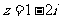 ,那么
,那么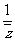 =
=
(A)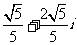 (B)
(B)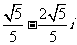 (C)
(C)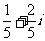 (D)
(D)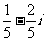
(3)已知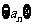 为等差数列,且
为等差数列,且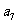 -2
-2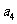 =-1,
=-1, 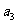 =0,则公差d=
=0,则公差d=
(A)-2 (B)-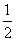 (C)
(C)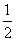 (D)2
(D)2
(4)平面向量a与b的夹角为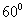 ,a=(2,0), | b |=1,则 | a+2b |=
,a=(2,0), | b |=1,则 | a+2b |=
(A)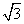 (B)2
(B)2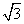 (C)4 (D)12
(C)4 (D)12
(5)如果把地球看成一个球体,则地球上的北纬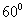 纬线长和赤道长的比值为
纬线长和赤道长的比值为
0.(A)0.8 (B)75 (C)0.5 (D)0.25
(6) 已知函数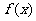 满足:x
满足:x 4,则
4,则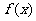 =
=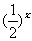 ;当x<4时
;当x<4时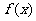 =
=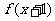 ,则
,则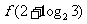 =
=
(A)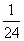 (B)
(B)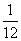 (C)
(C)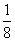 (D)
(D)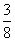
(7) 已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C
的方程为
(A)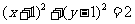 (B)
(B) 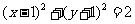
(C)
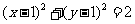 (D)
(D) 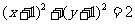

10)某店一个月的收入和支出总共记录了 N个数据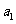 ,
,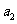 ,。。。
,。。。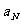 ,其中收入记为
,其中收入记为
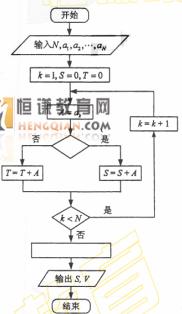
正数,支出记为负数。该店用右边的程序框图计算月总收入S和月净盈利V,那么在图中空白的判断框和处理框中,应分别填入下列四个选项中的
(A)A>0,V=S-T
(B) A<0,V=S-T
(C) A>0, V=S+T
(D)A<0, V=S+T
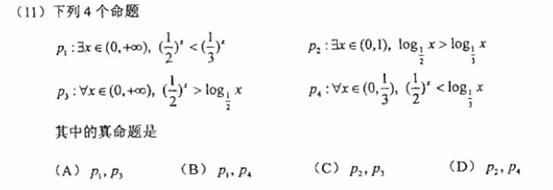
(12)已知偶函数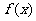 在区间
在区间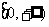 单调增加,则满足
单调增加,则满足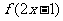 <
<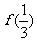 的x 取值范围是
的x 取值范围是
(A)(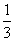 ,
,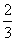 ) (B) [
) (B) [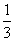 ,
,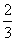 ) (C)y=(
) (C)y=(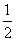 ,
,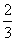 ) (D) [
) (D) [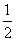 ,
,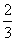 )
)
2009年普通高等学校招生全国统一考试(辽宁卷)
数学(文科类)
第II卷
二-填空题:本大题共4小题,每小题5分。
(13)在平面直角坐标系xoy中,四边形ABCD的边AB//DC,AD//BC,已知点A(-2,0),B(6,8),C(8,6),则D点的坐标为___________.
(14)已知函数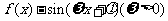 的图象如图所示,
的图象如图所示,
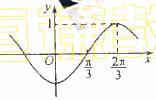
则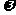 =
= 
(15)若函数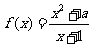 在
在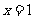 处取极值,则
处取极值,则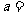
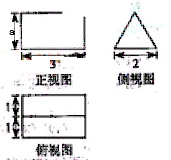
(16)设某几何体的三视图如下(尺寸的长度单位为m)。
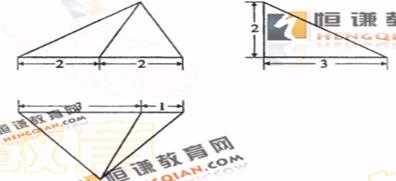
则该几何体的体积为 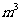
(17)(本小题满分12分)
在⊿ABC中,BC=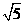 ,AC=3,sinC=2sinA
,AC=3,sinC=2sinA
(I) 求AB的值:
(II) 求sin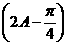 的值
的值
(18)(本小题满分12分)
在10件产品中,有3件一等品,4件二等品,3件三等品。从这10件产品中任取3件,求:
(I) 取出的3件产品中一等品件数X的分布列和数学期望;
(II) 取出的3件产品中一等品件数多于二等品件数的概率。
(19)(本小题满分12分)
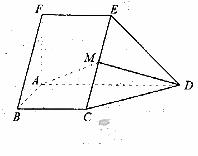 如图,在五面体ABCDEF中,FA
如图,在五面体ABCDEF中,FA 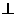 平面ABCD, AD//BC//FE,AB
平面ABCD, AD//BC//FE,AB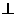 AD,M为EC的中点,AF=AB=BC=FE=
AD,M为EC的中点,AF=AB=BC=FE=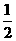 AD
AD
(I) 求异面直线BF与DE所成的角的大小;
(II) 证明平面AMD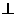 平面CDE;
平面CDE;
(III)求二面角A-CD-E的余弦值。
(20)(本小题满分12分)
已知函数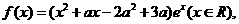 其中
其中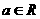
(1) 当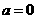 时,求曲线
时,求曲线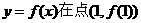 处的切线的斜率;
处的切线的斜率;
(2) 当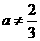 时,求函数
时,求函数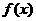 的单调区间与极值。
的单调区间与极值。
(21)(本小题满分14分)
以知椭圆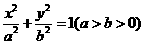 的两个焦点分别为
的两个焦点分别为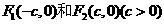 ,过点
,过点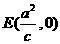 的直线与椭圆相交与
的直线与椭圆相交与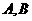 两点,且
两点,且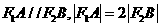 。
。
(1) 求椭圆的离心率;
(2) 求直线AB的斜率;
(3) 设点C与点A关于坐标原点对称,直线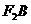 上有一点
上有一点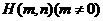 在
在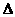
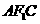 的外接圆上,求
的外接圆上,求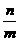 的值
的值
(22)(本小题满分14分)
已知等差数列{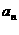 }的公差为d(d
}的公差为d(d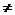 0),等比数列{
0),等比数列{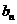 }的公比为q(q>1)。设
}的公比为q(q>1)。设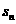 =
=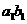 +
+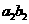 …..+
…..+ 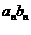 ,
,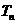 =
=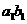 -
-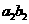 +…..+(-1
+…..+(-1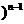
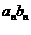 ,n
,n
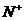
(I)
若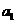 =
=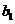 = 1,d=2,q=3,求
= 1,d=2,q=3,求 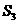 的值;
的值;
(II)
若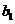 =1,证明(1-q)
=1,证明(1-q)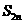 -(1+q)
-(1+q)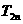 =
=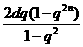 ,n
,n
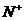 ;
;
(Ⅲ) 若正数n满足2 n
n q,设
q,设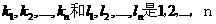 的两个不同的排列,
的两个不同的排列, 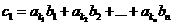 ,
, 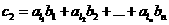 证明
证明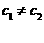 。
。
本资料由《七彩教育网》 提供!
 (11)某学院的A,B,C三个专业共有1200名学生,为了调
(11)某学院的A,B,C三个专业共有1200名学生,为了调
查这些学生勤工俭学的情况,拟采用分层抽样的方法抽取
一个容量为120的样本。已知该学院的A专业有380名学生,
B专业有420名学生,则在该学院的C专业应抽取____名学生。
(12)如图是一个几何体的三视图,若它的体积是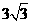 ,则
,则
a=_______
(13) 设直线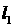 的参数方程为
的参数方程为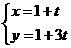 (t为参数),直线
(t为参数),直线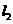 的方程为y=3x+4则
的方程为y=3x+4则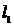 与
与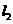 的距离为_______
的距离为_______
(14)若圆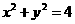 与圆
与圆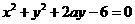 (a>0)的公共弦的长为
(a>0)的公共弦的长为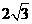 ,
,
则a=___________
(15)在四边形ABCD中,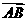 =
=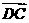 =(1,1),
=(1,1),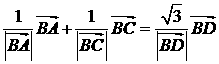 ,则四边形ABCD的面积是
,则四边形ABCD的面积是
(16)用数字0,1,2,3,4,5,6组成没有重复数字的四位数,其中个位、十位和百位上的数字之和为偶数的四位数共有 个(用数字作答)
22. (本小题满分14分)
已知椭圆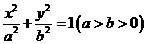 的两个焦点分别为
的两个焦点分别为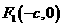 和
和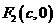 ,过点
,过点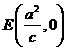 的直线与椭圆相交于
的直线与椭圆相交于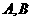 两点,且
两点,且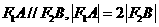
(1)求椭圆的离心率
(2)求直线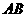 的斜率
的斜率
(3)设点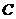 与点
与点 关于坐标原点对称,直线
关于坐标原点对称,直线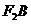 上有一点
上有一点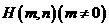 在
在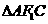 的外接圆上,求
的外接圆上,求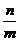 的值
的值
本资料由《七彩教育网》 提供!
21. (本小题满分14分)
设函数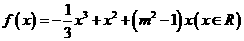 ,其中
,其中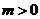
(1)当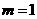 时,求曲线
时,求曲线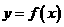 在点
在点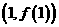 处的切线的斜率
处的切线的斜率
(2)求函数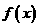 的单调区间与极值
的单调区间与极值
(3)已知函数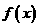 有三个互不相同的零点
有三个互不相同的零点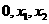 ,且
,且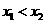 ,若对任意的
,若对任意的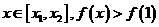 恒成立,求
恒成立,求 的取值范围
的取值范围
20. (本小题满分12分)
已知等差数列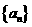 的公差不为0.设
的公差不为0.设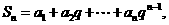
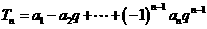
(1)若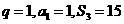 ,求数列
,求数列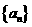 的通项公式
的通项公式
(2)若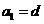 ,且
,且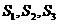 成等比数列,求
成等比数列,求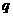 的值
的值
(3)若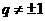 ,证明
,证明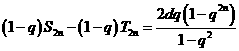
19. (本小题满分12分)
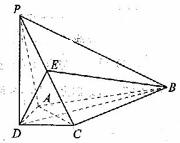 如图,在四棱锥
如图,在四棱锥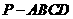 中,
中,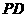
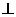 平面
平面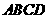 ,
,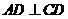 ,
,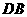 平分
平分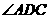 ,
,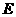 为的
为的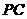 中点,
中点,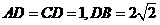
(1)证明: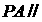 平面
平面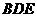
(2)证明: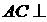 平面
平面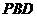
(3)求直线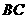 与平面
与平面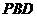 所成角的正切值
所成角的正切值
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com