
题目列表(包括答案和解析)
22. 解:(1) 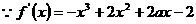
由题意可得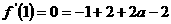
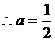 …………………2分
…………………2分
(2)由(1)知
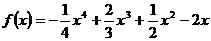
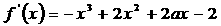 =
=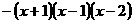
由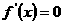 得
得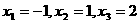
当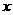 变化时,
变化时,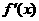 与
与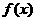 的变化情况如下表:
的变化情况如下表:
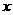 |
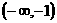 |
-1 |
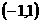 |
1 |
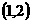 |
2 |
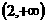 |
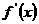 |
+ |
0 |
-- |
0 |
+ |
0 |
--- |
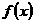 |
 |
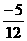 |
 |
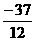 |
 |
 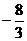 |
 |
从而可知,当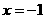 时,函数
时,函数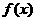 取得极大值
取得极大值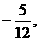
当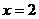 时, 函数
时, 函数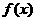 取得极大值
取得极大值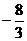 ,极小值
,极小值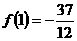
作出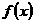 的大致图像
的大致图像
因关于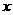 的方程
的方程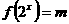 有三个不同的实数解,令
有三个不同的实数解,令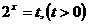 ,即关于
,即关于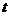 的方程
的方程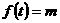 在
在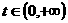 上有三个不同的实数解.即
上有三个不同的实数解.即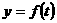 的图像与直线
的图像与直线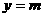 在
在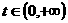 上有三个不同的交点,而
上有三个不同的交点,而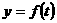 的图像与
的图像与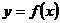 的图像一致.又有
的图像一致.又有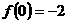 ,由图可知,
,由图可知,
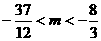 ……………………7分
……………………7分
(3)当函数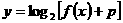 的图像与坐标轴无交点,分以下两种情况:
的图像与坐标轴无交点,分以下两种情况:
(1) 当函数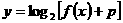 的图像与
的图像与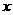 轴无交点时,则必须有
轴无交点时,则必须有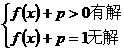 ,即
,即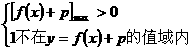 ,
,
而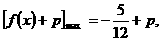 函数
函数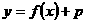 的值域为
的值域为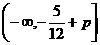 ,
,

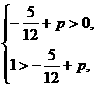 解得
解得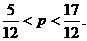
(2)当函数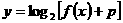 的图像与
的图像与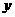 轴无交点时,则必须有
轴无交点时,则必须有
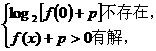 即
即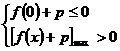 ,即
,即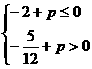
解得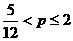 ,
,
综上, 实数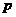 的取值范围为
的取值范围为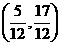 ………………….14分
………………….14分
21、(1)设椭圆C的方程为
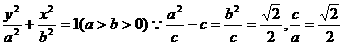
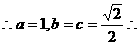 椭圆C的方程为
椭圆C的方程为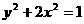 ………………4分
………………4分
(2)由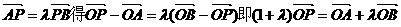
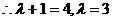 设
设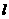 与椭圆C交点为
与椭圆C交点为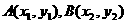
将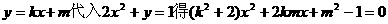
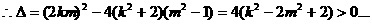 ①
①
则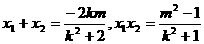
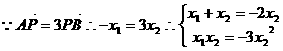
消去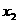 得
得 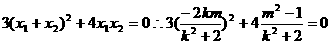
即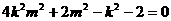
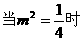
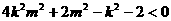
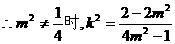 由①得
由①得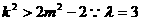
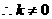
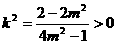
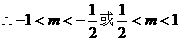
综上所述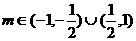 ………………………………12分
………………………………12分
20、(1)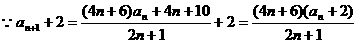
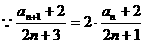
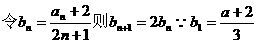
当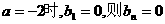
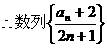 不是等比数列,
不是等比数列,
当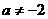 时,
时,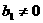 ,数列
,数列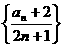 是等比数列且公比为2,………4分
是等比数列且公比为2,………4分
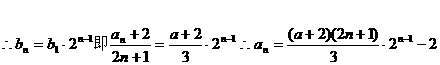 ……6分
……6分
(2)由(1)得当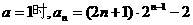
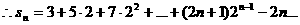 1°
1°
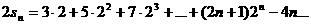 2°
2°
1°-2°及-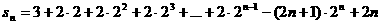
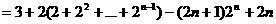
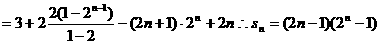 ………12分
………12分
19、19.解法一:(1)易求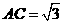 ,从而
,从而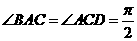 ,由三垂线定理知:
,由三垂线定理知: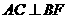 。………3分
。………3分
(2)法一:易求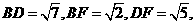 由勾股定理知
由勾股定理知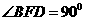 ,设点
,设点 在面
在面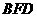 内的射影为
内的射影为 ,过
,过 作
作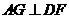 于
于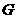 ,连结
,连结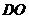 ,则
,则 为二面角
为二面角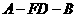 的平面角。在
的平面角。在 中由面积法易求
中由面积法易求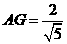 ,由体积法求得点
,由体积法求得点 到面
到面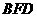 的距离是
的距离是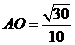 ,所以
,所以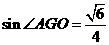 ,所以求二面角
,所以求二面角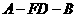 的大小为
的大小为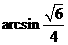 。………8分
。………8分
法二:易求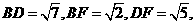 由勾股定理知
由勾股定理知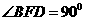 ,过
,过 作
作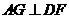 于
于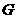 ,又过
,又过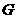 作
作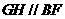 交
交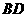 于
于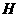 ,连结
,连结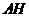 。则易证
。则易证 为二面角
为二面角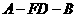 的平面角。在
的平面角。在 中由面积法易求
中由面积法易求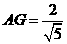 ,从而
,从而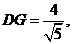 于是
于是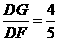 ,所以
,所以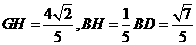 ,在
,在 中由余弦定理求得
中由余弦定理求得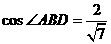 。再在
。再在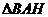 中由余弦定理求得
中由余弦定理求得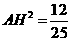 。最后在
。最后在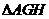 中由余弦定理求得
中由余弦定理求得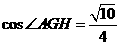 ,所以求二面角
,所以求二面角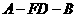 的大小为
的大小为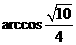 。
。
(3)设AC与BD交于O,则OF//CM,所以CM//平面FBD,当P点在M或C时,三棱锥P-BFD的体积的最小。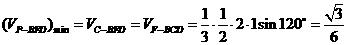 。………12分
。………12分
解法二:空间向量解法,略。
18. 解:(1)设袋中数学题的个数为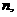 则
则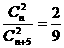 …………2分
…………2分
化简: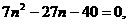
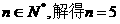 ,即有5个数学题。…6分
,即有5个数学题。…6分
(2)由题知A.B.C.D,4个题中该生做 对2题,做错2题,其中:
A.B.C在三题中做对1个做错2个而D题做对的概率为:
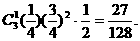 …………8分
…………8分
A.B.C三题中做对2个做错1个而D题做错的概率为:
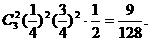 …………10分
…………10分
由互斥事件概率公式知所求概率为:
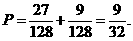 …………12分
…………12分
17.(本题满分12分)
解:(1)f(x)=1+cos2x+sin2x=2sin(2x+)+1. …………………2分
因为-≤x≤,所以-≤2x+≤.……………4分
所以-≤sin(2x+)≤1.所以-1≤2sin(2x+)≤2
所以f(x)∈[0,3].即函数f(x)在[-,]上的值域为[0,3].………6分
(2)由f(C)=2得,2sin(2C+)+1=2,所以sin(2C+)=.
在△ABC中,因为0<C<p,所以<2C+<.
所以2C+=.所以C=,所以A+B=.………………………8分
因为2sinB=cos(A-C)-cos(A+C).所以2sinB=2sinAsinC. ………10分
因为B=-A,C=.所以2sin(-A)=sinA.
即cosA+sinA=sinA.即(-1)sinA=cosA.
所以tanA===.……………………12分
13、119 14、80 15、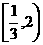 16、①④
16、①④
22. (本题满分14分)
(本题满分14分)
已知函数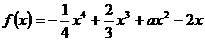 ,在区间
,在区间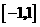 上为减函数,在区间
上为减函数,在区间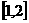 上为增函数。
上为增函数。
(I)求实数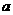 的值;
的值;
(II)若关于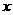 的方程
的方程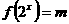 有三个不同实数解,求实数
有三个不同实数解,求实数 的取值范围;
的取值范围;
(III)若函数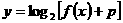 的图像与坐标轴无交点,求实数
的图像与坐标轴无交点,求实数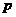 的取值范围;
的取值范围;
四川省江油市2009级高考适应性考试
数 学(文史类)
一选择题:本大共12小题,每小题5分,在每小题的四个选项中只有一个是正确的.
21、 (本题满分12分)椭圆C的中心在原点O,焦点在
(本题满分12分)椭圆C的中心在原点O,焦点在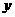 轴上,焦点到相应准线的距离以及离心率均为
轴上,焦点到相应准线的距离以及离心率均为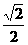 ,直线
,直线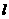 与
与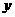 轴交于点
轴交于点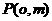 与椭圆C交于相异两点A、B且
与椭圆C交于相异两点A、B且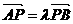 。
。
(1)求椭圆方程;
(2)若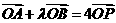 ,求
,求 的取值范围。
的取值范围。
20、(本题满分12分)已知数列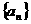 满足
满足
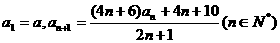
(1)试判断数列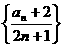 是否为等比数列?若不是,说明理由?若是,求通项
是否为等比数列?若不是,说明理由?若是,求通项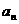 ;
;
(2)如果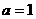 时,数列
时,数列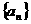 的前n项和为
的前n项和为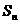 ,求
,求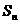
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com