
题目列表(包括答案和解析)
4.若向量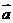 ,
,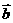 满足
满足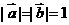 ,且
,且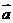 ·
·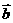 +
+
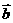 ·
·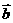 =
=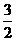 ,则向量
,则向量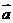 、
、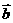 的夹角为( )
的夹角为( )
A.30° B.45°
C.60° D.90°
3.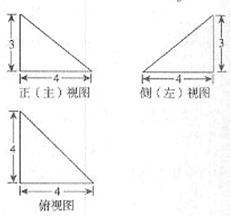 右图是一个几何体的三视图,则该几何体
右图是一个几何体的三视图,则该几何体
的体积为( )
A.6
B.8
C.16
D.24
2.下列函数中,在其定义域内既是奇函数又是减函数的是( )
A.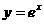 B.
B.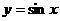 C.
C.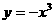 D.
D.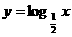
1.设全集U=R,集合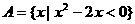 ,
,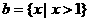 ,则集合A
,则集合A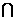 CUB=( )
CUB=( )
A.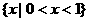 B.
B.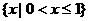
C.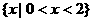 D.
D.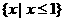
21.解:(Ⅰ)由题意知抛物线的焦点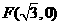
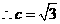 ……………………………………………………………………………1分
……………………………………………………………………………1分
又 椭圆的短轴的两个端点与
椭圆的短轴的两个端点与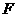 构成正三角形
构成正三角形
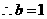
 椭圆的方程为
椭圆的方程为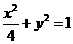 ……………………………………………………3分
……………………………………………………3分
(Ⅱ)当直线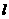 的斜率存在时,设其斜率为
的斜率存在时,设其斜率为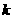 ,则
,则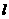 的方程为:
的方程为: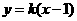
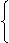
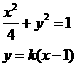
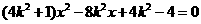
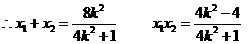 ………………………………………5分
………………………………………5分
则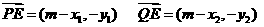

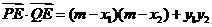
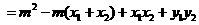
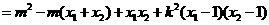
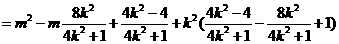
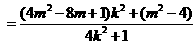 ……………………………………7分
……………………………………7分
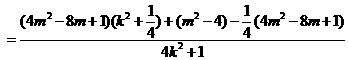
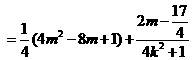 ……………………………………9分
……………………………………9分
当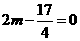 即
即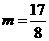 时
时 为定值
为定值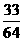 …………………………10分
…………………………10分
当直线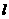 的斜率不存在时,
的斜率不存在时,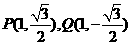
由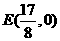 可得
可得
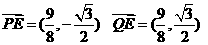
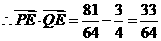
综上所述当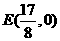 时,
时,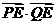 为定值
为定值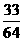 ……………………………………12分
……………………………………12分
21.(本小题满分12分)
已知椭圆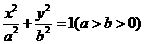 的一个焦点与抛物线
的一个焦点与抛物线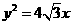 的焦点
的焦点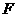 重合,且椭圆短轴的两个端点与
重合,且椭圆短轴的两个端点与 构成正三角形。
构成正三角形。
(Ⅰ)求椭圆的方程;
(Ⅱ)若过点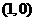 的直线
的直线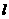 与椭圆交于不同两点
与椭圆交于不同两点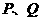 ,试问在
,试问在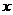 轴上是否存在定点
轴上是否存在定点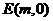 ,使
,使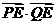 恒为定值?若存在,求出
恒为定值?若存在,求出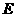 的坐标及定值;若不存在,请说明理由。
的坐标及定值;若不存在,请说明理由。
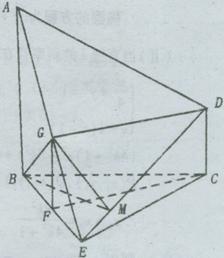
20.解:(Ⅰ)当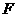 为
为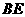 的中点时,
的中点时,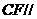 平面
平面 ………………………………………1分
………………………………………1分
证明:取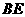 的中点
的中点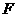 、
、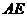 的中点
的中点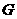 ,连结
,连结
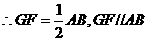
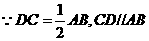 B
B
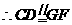
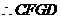 是平行四边形……………………3分
是平行四边形……………………3分
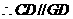
 平面
平面 …………………………4分
…………………………4分
(Ⅱ) 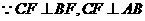
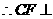 平面
平面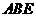
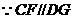
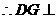 平面
平面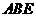 ……………………………………………………………………6分
……………………………………………………………………6分
 平面
平面
 平面
平面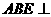 平面
平面 ……………………………………………………………7分
……………………………………………………………7分
(Ⅲ) 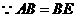
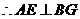
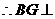 平面
平面
过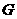 作
作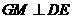 ,连结
,连结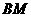 ,则
,则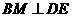
则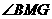 为二面角
为二面角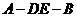 的平面角………………………………………9分
的平面角………………………………………9分
设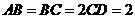 ,则
,则
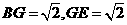
在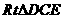 中,
中,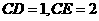
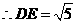
又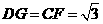
由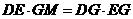 得
得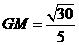 …………………………………………11分
…………………………………………11分
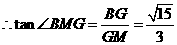
 面角
面角 的正切值
的正切值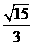 ………………………………………………12分
………………………………………………12分
20. (本小题满分12分)
(本小题满分12分)
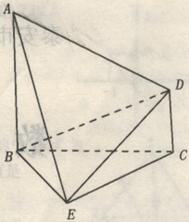
如图,已知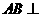 平面
平面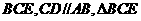 是正三角
是正三角
形,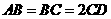 。
。
(Ⅰ)在线段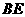 上是否存在一点
上是否存在一点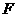 ,使
,使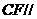 平面
平面 ?
?
(Ⅱ)求证:平面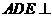 平面
平面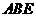 ;
;
(Ⅲ)求二面角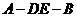 的正切值。
的正切值。
18.解:(Ⅰ) 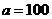
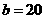
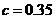
由频率分布表可得成绩不低予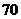 分的概率为:
分的概率为:
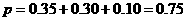 ……………………………………………………………4分
……………………………………………………………4分
(Ⅱ)由频率分布表可知,“成绩低予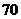 分”的概率为
分”的概率为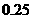
 按成绩分层抽样抽取
按成绩分层抽样抽取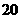 人时.“成绩低于
人时.“成绩低于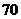 分”的应抽取
分”的应抽取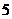 人………………6分
人………………6分
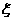 的取值为
的取值为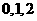
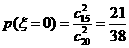
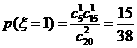
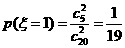
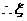 的分布列为
的分布列为
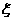

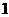
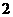
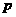
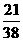
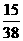
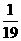
………………………………………………………9分
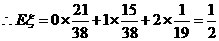 ………………………………………………12分
………………………………………………12分
18.(本小题满分12分)
某校举行了“环保知识竞赛”,为了解本次竞赛成 频率分布表
|
分组 |
频数 |
频率 |
|
[50,60) |
5 |
0.05 |
|
[60,70) |
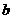 |
0.20 |
|
[70,80) |
35 |
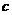 |
|
[80,90) |
30 |
0.30 |
|
[90,100) |
10 |
0.10 |
|
合计 |
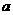 |
1.00 |
绩情况,从中随机抽取部分学生的成绩(得分均为整数,
满分100分),进行统计,请根据频率分布表中所提供
的数据,解答下列问题:
(Ⅰ)求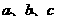 的值及随机抽取一考生其成绩不
的值及随机抽取一考生其成绩不
低于70分的概率;
(Ⅱ)按成绩分层抽样抽取20人参加社区志愿者活
动,并从中指派2名学生担任负责人,记这2名学生中
“成绩低于70分”的人数为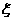 ,求
,求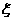 的分布列及期望。
的分布列及期望。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com