
题目列表(包括答案和解析)
3.如果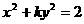 表示焦点在
表示焦点在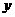 轴上的椭圆,那么实数
轴上的椭圆,那么实数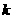 的取值范围是( )
的取值范围是( )
A.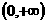 B.
B.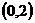 C.
C.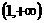 D.
D.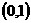
2.若椭圆的对称轴为坐标轴,长轴长与短轴长的和为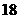 ,焦距为
,焦距为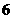 ,则椭圆的方程为( )
,则椭圆的方程为( )
A.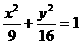 B.
B.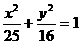
C.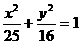 或
或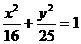 D.以上都不对
D.以上都不对
1. 已知椭圆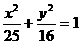 上的一点
上的一点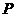 到椭圆一个焦点的距离为
到椭圆一个焦点的距离为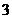 ,则
,则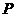 到另一焦点距离为( )
到另一焦点距离为( )
A.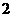 B.
B.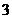 C.
C.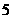 D.
D.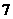
12.(1)由题意,可设所求椭圆的标准方程为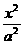 +
+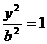
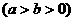 ,其半焦距
,其半焦距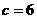 。
。
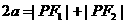
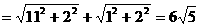 , ∴
, ∴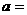
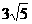 ,
,
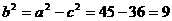 ,故所求椭圆的标准方程为
,故所求椭圆的标准方程为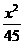 +
+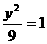 ;
;
(2)点P(5,2)、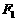 (-6,0)、
(-6,0)、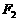 (6,0)关于直线y=x的对称点分别为:
(6,0)关于直线y=x的对称点分别为:
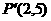 、
、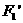 (0,-6)、
(0,-6)、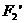 (0,6)
(0,6)
设所求双曲线的标准方程为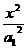 -
-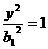
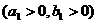 ,由题意知半焦距
,由题意知半焦距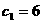 ,
,
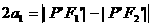
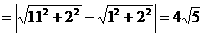 , ∴
, ∴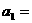
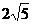 ,
,
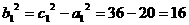 ,故所求双曲线的标准方程为
,故所求双曲线的标准方程为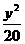 -
-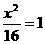 .
.
11.解:由共同的焦点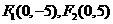 ,可设椭圆方程为
,可设椭圆方程为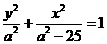 ;
;
双曲线方程为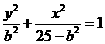 ,点
,点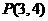 在椭圆上,
在椭圆上,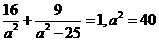
双曲线的过点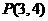 的渐近线为
的渐近线为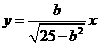 ,即
,即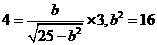
所以椭圆方程为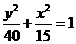 ;双曲线方程为
;双曲线方程为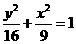
10.
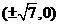 渐近线方程为
渐近线方程为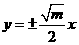 ,得
,得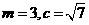 ,且焦点在
,且焦点在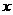 轴上.
轴上.
9.
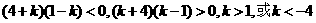 .
.
8.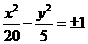 设双曲线的方程为
设双曲线的方程为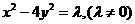 ,焦距
,焦距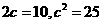
当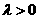 时,
时,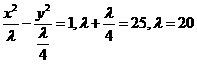 ;
;
当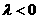 时,
时,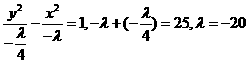
7.D.由题意知,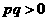 .若
.若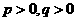 ,则双曲线的焦点在
,则双曲线的焦点在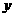 轴上,而在选择支A,C中,椭圆的焦点都在
轴上,而在选择支A,C中,椭圆的焦点都在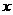 轴上,而选择支B,D不表示椭圆;
轴上,而选择支B,D不表示椭圆;
若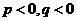 ,选择支A,C不表示椭圆,双曲线的半焦距平方
,选择支A,C不表示椭圆,双曲线的半焦距平方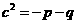 ,双曲线的焦点在
,双曲线的焦点在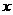 轴上,选择支D的方程符合题意.
轴上,选择支D的方程符合题意.
6. C[思路分析]:由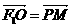 知四边形
知四边形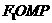 是平行四边形,又
是平行四边形,又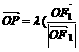
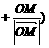 知
知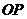 平分
平分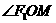 ,即
,即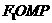 是菱形,设
是菱形,设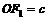 ,则
,则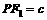 .
.
又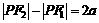 ,∴
,∴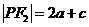 ,由双曲线的第二定义知:
,由双曲线的第二定义知: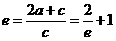 ,且
,且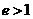 ,∴
,∴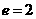 ,故选
,故选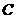 .
.
[命题分析]:考查圆锥曲线的第一、二定义及与向量的综合应用,思维的灵活性.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com