
题目列表(包括答案和解析)
1.设a=2-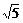 ,b=
,b=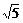 -2,c=5-2
-2,c=5-2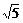 ,则a、b、c之间的大小关系为____________.
,则a、b、c之间的大小关系为____________.
解析:a=2-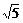 =
=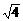 -
-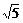 <0,∴b>0.c=5-2
<0,∴b>0.c=5-2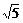 =
=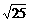 -
-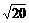 >0.
>0.
b-c=3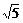 -7=
-7=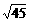 -
-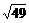 <0.∴c>b>a.答案:c>b>a
<0.∴c>b>a.答案:c>b>a
3、判断符号;4、作出结论.
[新题导练].
1、作差;2、变形:配方、因式分解、通分、分母(分子)有理化等;
8.今有一块边长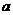 的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,
的正三角形的厚纸,从这块厚纸的三个角,按右图那样切下三个全等的四边形后,做成一个无盖的盒子,要使这个盒子容积最大,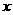 值应为多少?
值应为多少?
解:折成盒子后底面正三角形的边长为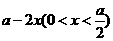 ,高为
,高为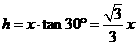
设:容积为V,则
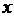

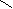
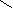

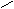
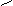
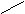
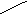

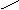




|

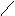






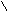

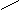
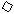
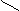
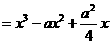


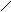
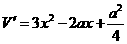
令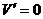 得
得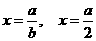 (舍去)
(舍去)
当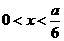 时,
时,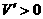 ;当
;当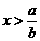 时,
时,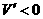
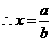 时,
时,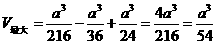
答: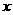 为
为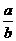 时,盒子的容积最大为
时,盒子的容积最大为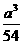
|

|
版权所有:()
版权所有:()
7. (广东省2008届六校第二次联考)设某物体一天中的温度T是时间t的函数,已知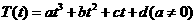 ,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
,其中温度的单位是℃,时间的单位是小时.中午12:00相应的t=0,中午12:00以后相应的t取正数,中午12:00以前相应的t取负数(如早上8:00相应的t=-4,下午16:00相应的t=4).若测得该物体在早上8:00的温度为8℃,中午12:00的温度为60℃,下午13:00的温度为58℃,且已知该物体的温度早上8:00与下午16:00有相同的变化率.
(1)求该物体的温度T关于时间t的函数关系式;
(2)该物体在上午10:00到下午14:00这段时间中(包括端点)何时温度最高?最高温度是多少?
解:(1) 因为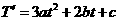 , ………………………2分
, ………………………2分
而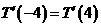 , 故
, 故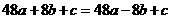 , ………………………3分
, ………………………3分

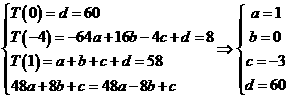 . …………………6分
. …………………6分
∴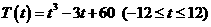 . …………………………………7分
. …………………………………7分
(2) 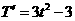 , 由
, 由 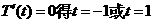 ……………………9分
……………………9分
当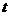 在
在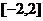 上变化时,
上变化时, 的变化情况如下表:
的变化情况如下表:
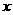 |
-2 |
(-2,-1) |
-1 |
(-1,1) |
1 |
(1,2) |
2 |
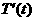 |
|
+ |
0 |
- |
0 |
+ |
|
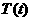 |
58 |
增函数 |
极大值62 |
减函数 |
极小值58 |
增函数 |
62 |
…………………………………12分
由上表知当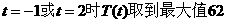 ,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
,说明在上午11:00与下午14:00,该物体温度最高,最高温度是62℃.
6.在长为100千米的铁路线AB旁的C处有一个工厂,工厂与铁路的距离CA为20千米.由铁路上的B处向工厂提供原料,公路与铁路每吨千米的货物运价比为5∶3,为节约运费,在铁路的D处修一货物转运站,设AD距离为x千米,沿CD直线修一条公路(如图).
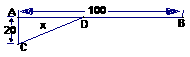 (1)将每吨货物运费y(元)表示成x的函数.
(1)将每吨货物运费y(元)表示成x的函数.
(2)当x为何值时运费最省?
解:(1)设公路与铁路每吨千米的货物运价分别为5k、3k(元)(k为常数)AD=x,则DB=100-x.
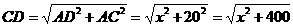
∴每吨货物运费y=(100-x)·3k+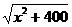 ·5k(元)
·5k(元)
(2)令y′=-3k+5k·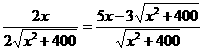 ·k=0
·k=0
∴5x-3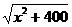 =0
=0
∵x>0,∴解得x=15
当0<x<15时,y′<0;当x>15时,y′>0
∴当x=15时,y有最小值.
答:当x为15千米时运费最省 .
5. 质量为5 kg的物体运动的速度为v=(18t-3t2) m/s,在时间t=2 s时所受外力为______N.
分析:本题主要考查导数的物理意义即速度v(t)对时间的导数是该时刻的加速度.
解:∵v′=18-6t,∴v′|t=2=18-6×2=6.∴t=2时物体所受外力F为6×5=30.
综合拔高训练
4. 要做一个圆锥形漏斗,其母线长为20cm,要使体积为最大,则其高应为____________.
|
|

|
 解:设圆锥底面半径为r,高为
解:设圆锥底面半径为r,高为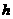 ,则
,则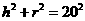 ,
, ,
, 圆锥体积一天
圆锥体积一天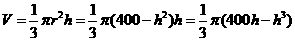 ,令
,令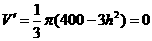 得
得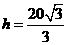 ,当
,当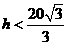 时,
时,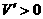 ;
;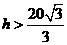 时,
时,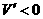

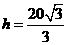 时,V最大,当应填
时,V最大,当应填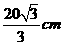
3.要建造一个长方体形状的仓库,其内部的高为3m,长和宽的和为20m,则仓库容积的最大值为 1800m3 .
解:设长为 ,则宽为
,则宽为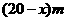 ,仓库的容积为V
,仓库的容积为V
则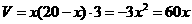
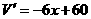 ,令
,令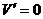 得
得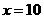
当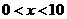 时,
时,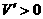 ;当
;当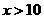 时,
时,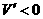

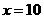 时,
时,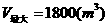
2.(2008·深圳6校)某日中午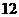 时整,甲船自
时整,甲船自 处以
处以 的速度向正东行驶,乙船自
的速度向正东行驶,乙船自 的正北
的正北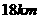 处以
处以 的速度向正南行驶,则当日
的速度向正南行驶,则当日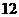 时
时 分时两船之间距离对时间的变化率是_____________.
分时两船之间距离对时间的变化率是_____________.
解析:距离对时间的变化率即瞬时速度。即此时距离函数对时间变量的导数。将物理学概念与数学中的导数概念迁移到实际应用题中来。易求得从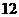 点开始,
点开始,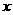 小时时甲乙两船的距离
小时时甲乙两船的距离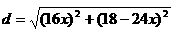
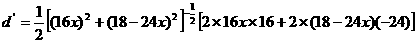 ,
,
当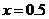 时,
时,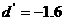
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com