
题目列表(包括答案和解析)
7、若曲线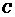 :
: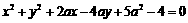 上所有的点均在第二象限内,则
上所有的点均在第二象限内,则 的取值范围为( )
的取值范围为( )
A.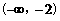 B.
B.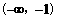
C.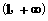 D.
D.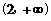
6、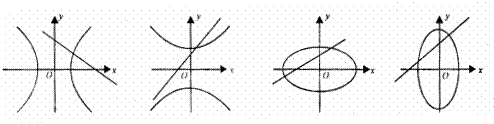 已知方程
已知方程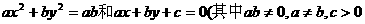 ,它们所表示的曲线可能是(
)
,它们所表示的曲线可能是(
)
A. B. C. D.
5、一个体积为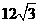 的正三棱柱的三视图如图所示,则这个
的正三棱柱的三视图如图所示,则这个
三棱柱的左视图的面积为( )
A.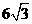 B.8
B.8
C.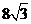 D.12
D.12
4、已知等差数列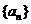 的前
的前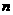 项和为
项和为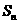 ,且满足
,且满足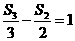 ,则数列
,则数列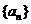 的公差是( )
的公差是( )
 A.
A.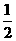 B.1 C.2 D.3
B.1 C.2 D.3
3、设0<x<1,则a=2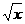 ,b=1+x, c=
,b=1+x, c=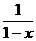 中最大的一个是( )
中最大的一个是( )
A.a B.b C.c D.不能确定
2、设集合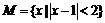 ,
,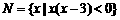 ,那么“
,那么“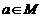 ”是“
”是“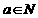 ”的( )
”的( )
A.必要而不充分条件 B.充分而不必要条件
C.充分必要条件 D.既不充分也不必要条件
1、设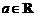 ,若
,若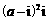 (
( 为虚数单位)为正实数,则
为虚数单位)为正实数,则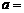 ( )
( )
A.2 B.1 C.0 D.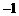
8. (广东省惠州市2009届高三第二次调研考试)
设单调递增函数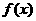 的定义域为
的定义域为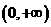 ,且对任意的正实数x,y有:
,且对任意的正实数x,y有: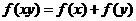 且
且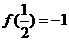 .
.
⑴、一个各项均为正数的数列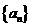 满足:
满足: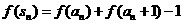 其中
其中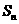 为数列
为数列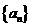 的前n项和,求数列
的前n项和,求数列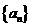 的通项公式;
的通项公式;
⑵、在⑴的条件下,是否存在正数M使下列不等式:
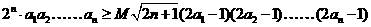
对一切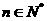 成立?若存在,求出M的取值范围;若不存在,请说明理由.
成立?若存在,求出M的取值范围;若不存在,请说明理由.
.解:⑴、 对任意的正数
对任意的正数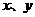 均有
均有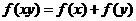 且
且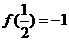 .
.
又
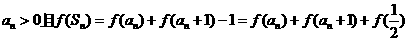

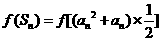 ,
,
又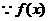 是定义在
是定义在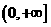 上的单增函数,
上的单增函数,
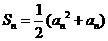 .
.
当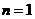 时,
时,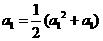 ,
,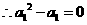 .
.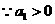 ,
,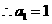 .
.
当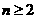 时,
时,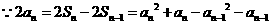 ,
,
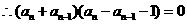 .
.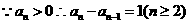 ,
,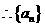 为等差数列,
为等差数列,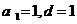 ,
,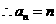 .
.
⑵、假设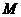 存在满足条件,
存在满足条件,
即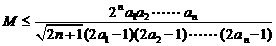 对一切
对一切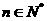 恒成立. ……………8分
恒成立. ……………8分
令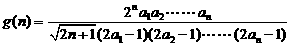 ,
,

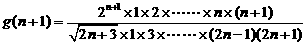 ,
,
故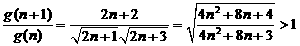 ,
,
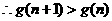 ,
,
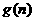 单调递增,
单调递增,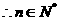 ,
,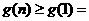
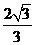 .
.

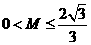 .
.

7.已知函数f(x)=|log2(x+1)|,实数m、n在其定义域内,且m<n,f(m)=f(n).
求证:(1)m+n>0;
(2)f(m2)<f(m+n)<f(n2).
(1)证法一:由f(m)=f(n),得|log2(m+1)|=|log2(n+1)|,即log2(m+1)=±log2(n+1),
log2(m+1)=log2(n+1), ①
或log2(m+1)=log2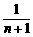 . ②
. ②
由①得m+1=n+1,与m<n矛盾,舍去.
由②得m+1=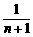 ,即(m+1)(n+1)=1. ③
,即(m+1)(n+1)=1. ③
∴m+1<1<n+1.∴m<0<n.∴mn<0.
由③得mn+m+n=0,m+n=-mn>0.
证法二:(同证法一得)(m+1)(n+1)=1.
∵0<m+1<n+1,∴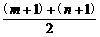 >
>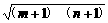 =1.∴m+n+2>2.∴m+n>0.
=1.∴m+n+2>2.∴m+n>0.
(2)证明:当x>0时,f(x)=|log2(x+1)|=log2(x+1)在(0,+∞)上为增函数.
由(1)知m2-(m+n)=m2+mn=m(m+n),且m<0,m+n>0,∴m(m+n)<0.
∴m2-(m+n)<0,0<m2<m+n.
∴f(m2)<f(m+n).
同理,(m+n)-n2=-mn-n2=-n(m+n)<0,
∴0<m+n<n2.∴f(m+n)<f(n2).
∴f(m2)<f(m+n)<f(n2).
6.某人乘坐出租车从A地到乙地,有两种方案:第一种方案,乘起步价为10元,每km价1.2元的出租车;第二种方案,乘起步价为8元,每km价1.4元的出租车,按出租车管理条例,在起步价内,不同型号的出租车行驶的里路是相等的,则此人从A地到B地选择哪一种方案比较适合?
解:设A地到B地距离为mkm,起步价内行驶的路为akm
显然,当m≤a时,选起步价为8元的出租车比较合适
当m>a时,设m=a+x(x>0),乘坐起步价为10元的出租车费用为P(x)元,乘坐起步价为8元的出租车费用为Q(x)元,则P(x)=10+1.2x,Q(x)=8+1.4x
∵ P(x)-Q(x)=2-0.2x=0.2(10-x)
∴ 当x>10时,P(x)<Q(x),此时起步价为10元的出租车比较合适
当x<10时,P(x)>Q(x),此时选起步价为8元的出租车比较合适
当x=10时,P(x)=Q(x),此时两种出租车任选
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com