18、(本小题满分12分)已知数列{a_n}的通项a_n=n，数列中的项按下列数表排列：

　　　　　　　　　　 1

　　　　　　　　　　 2　 3

　　　　　　　　　　 4　 5　 6

　　　　　　　　　　 7　 8　 9　 10

　　　　　　　　　　 11　 12　 13　 14　 15

　　　　　　　　　　 ……

⑴求第n行第一个数；

⑵求前n行各数之和。

19. 解：(1)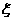的所有可能取值有6，2，1，-2；，

，

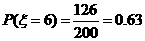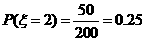
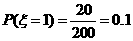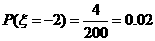
故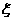的分布列为：

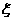	6	2	1	-2
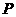	0.63	0.25	0.1	0.02

　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 4分

(2)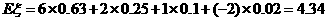　　　　　　　　 6分

(3)设技术革新后的三等品率为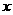，则此时1件产品的平均利润为

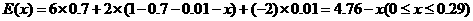
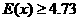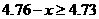依题意，，即，解得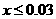

所以三等品率最多为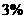 　　　　　　　　　　　　　　　　　　　　　　　12分

19．(本题满分12分)

随机抽取某厂的某种产品200件，经质检，其中有一等品126件、二等品50件、三等品20件、次品4件．已知生产1件一、二、三等品获得的利润分别为6万元、2万元、1万元，而1件次品亏损2万元．设1件产品的利润(单位：万元)为．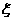

(1)求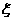的分布列；

(2)求1件产品的平均利润(即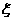的数学期望)；

(3)经技术革新后，仍有四个等级的产品，但次品率降为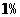，一等品率提高为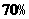．如果此时要求1件产品的平均利润不小于4.73万元，则三等品率最多是多少？

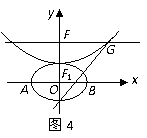
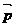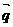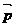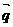14．将一颗骰子掷两次，观察出现的点数，并记第一次出现的点数为m,第二次出现的点数为n，向量=(m,n),=(3,6),则向量与共线的概率为　　　　　　　 。

答案：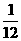 　　

19. 解：(1)共有10个等可能性的基本事件，列举如下：(1，2)，(1，3)，(1，4)，(1，5)，

　　　 (2，3)，(2，4)，(2，5)(3，4)，(3，5)，(4，5)。

(2)记事件“甲同学所抽取的两题的编号之和小于8但不小于4”为事件A

　　 由(1)可知事件共含有7个基本事件，列举如下：(1，3)，(1，4)，(1，5)，(2，3)，

(2，4)，(2，5)，(3，4)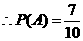

(3)记事件B“做对政治附加题同时还需做对两道基本题”

　　 记事件C“做对历史附加题同时还需至少做对一道基本题”

　　 记事件D“甲同学得分不低于20分”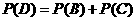

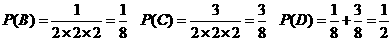
安徽师大附中2010届高三第一次摸底(理)

19．(本题满分12分)

现有编号分别为1，2，3的三个不同的政治基本题和一道政治附加题：另有编号分别为

4，5的两个不同的历史基本题和一道历史附加题。甲同学从这五个基本题中一次随即抽取两道题，每题做对做错及每题被抽到的概率是相等的。

　 (1)用符号(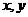)表示事件“抽到的两题的编号分别为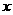、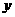，且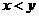”共有多少个基本事件？请列举出来：

　 (2)求甲同学所抽取的两道基本题的编号之和小于8但不小于4的概率。

　 (3)甲同学在抽完两道基本题之后又抽取一道附加题，做对基本题每题加5分，做对政治附加题加10分，做对历史附加题加15分，求甲同学得分不低于20分的概率。

4. 在抽查产品尺寸的过程中，将其尺寸分为若干组，并作出频率分布直方图。已知[a，b]是其中的一组，抽查出的个体在该组的频率为m，该组直方图的高为h，则|a-b|=(　　　 )

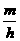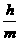A. hm　　 B. 　　　C. 　　　D.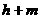 　

答案:B 　解析：有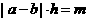得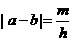

11、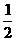

安徽省安庆市示范高中2010届高三五校协作调研模拟考试 数学理

(18) ( 本题满分12分 )已知一台机器在一天内发生故障的概率为0．2，机器发生故障时全天停止工作．一周五天工作日里无故障可获利10万元，发生一次故障可获利5万元，发生两次故障没有利润，发生三次或三次以上故障就要亏损2万元．这台机器在一周内平均获利多少？

(18)以ξ表示一周内机器发生故障的次数，则ξ~B(5，)，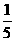

∴ P(ξ＝k)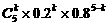＝ (k＝0、1、…、5)，

以η表示一周内获得的利润，则η＝g(ξ)，

而g(0)＝10，g(1)＝5，g(2)＝0，g(ξ≥3)＝－2

∴ P(η＝10)＝ P(ξ＝0)＝0．8⁵＝0．32828，

P(η＝5)＝ P(ξ＝1)＝0．4096，

P(η＝0)＝ P(ξ＝2)＝0．2048，

P(η＝－2)＝ P(ξ≥3)＝1－P(ξ＝0)－P(ξ＝1)－P(ξ＝2)＝0．05732，

∴ Eη＝10×0．328+5×0．410－2×0．057＝5．20896万元为所求

安徽师大附中2010届高三第一次摸底(文)

11．一只蚂蚁在三边边长分别为3，4，5的三角形的边上爬行，某时刻该蚂蚁距离三角形的三个顶点的距离均超过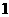的概率为　　　　　 。　

18．(1)记“编号的和为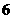”的事件，事件所包含的基本事件为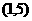、、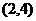、、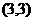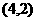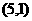，共5个， ∴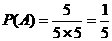

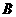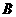(2)记“甲赢”为事件，事件所包含的基本事件为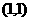、、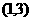、、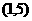、、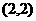、、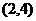、、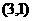、、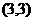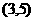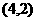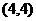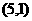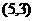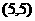，共13个， ∴，

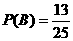安庆市示范高中2010届高三上学期四校元旦联考高三数学(理)测试