
题目列表(包括答案和解析)
23、 如图,在四棱锥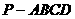 中,底面
中,底面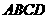 是
是
边长为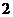 的菱形,
的菱形,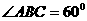 ,
,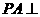 平面
平面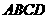 ,
,
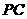 与平面
与平面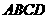 所成角的大小为
所成角的大小为 ,
,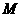 为
为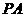 的中点.
的中点.
(1)求四棱锥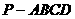 的体积;
的体积;
(2)求异面直线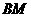 与
与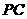 所成角的大小(结果用
所成角的大小(结果用
反三角函数表示).
2
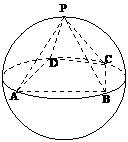 4、如图,正四棱锥
4、如图,正四棱锥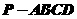 底面的四个顶点
底面的四个顶点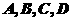 在球
在球 的同一个大圆上,点
的同一个大圆上,点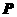 在球面上,且已知
在球面上,且已知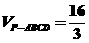 .
.
(1)求球 的表面积;
的表面积;
(2)设 为
为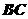 中点,求异面直线
中点,求异面直线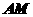 与
与 所成角的大小.
所成角的大小.
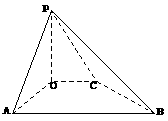 25 已知四边形
25 已知四边形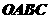 为直角梯形,
为直角梯形,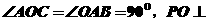 平面
平面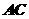 ,且
,且
(理)若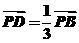 ,求:(1)点
,求:(1)点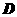 的坐标;
的坐标;
(2)异面直线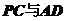 所成的角
所成的角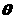 (用反三角函数值表示).
(用反三角函数值表示).
(文)(1)求证: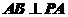 ;(2)求异面直线
;(2)求异面直线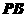 与
与 所成的角
所成的角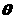
26 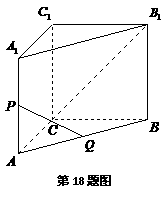 如图,在直三棱柱
如图,在直三棱柱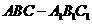 中,
中,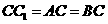 ,
,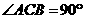 ,
,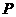 是
是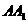 的中点,
的中点,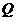 是
是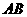 的中点.
的中点.
(1)求异面直线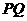 与
与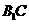 所成角的大小;
所成角的大小;
(2)若直三棱柱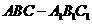 的体积为
的体积为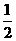 ,求四棱锥
,求四棱锥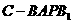 的体积.
的体积.
22.若圆锥的底面半径和高都是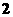 ,则圆锥的侧面积是_____________.
,则圆锥的侧面积是_____________.
18.如图所示,以圆柱的下底面为底面,并以圆柱的上底面圆心为顶点作圆锥,
则该圆锥与圆柱等底等高。若圆锥的轴截面是一个正三角形,则圆柱的
侧积面与圆锥的侧面积之比为
19已知圆锥的母线与底面所成角为600,高为3,则圆锥的侧面积为_________________.
20正方体中,连接相邻两个面的中心的连线可以构成一个美丽的几何体.若正方体的边长为1,则这个美丽的几何体的体积为_______________.
21在一个密封的容积为1的透明正方体容器内装有部分液体,如果任意转动该正方体,液面的形状都不可能是三角形,那么液体体积的取值范围是 。
17.若球的体积是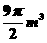 ,则球的表面积是____________
,则球的表面积是____________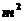 .
.
4.给出下列命题:(1)三点确定一个平面;(2)在空间中,过直线外一点只能作一条直线与该直线平行;(3)若平面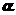 上有不共线的三点到平面
上有不共线的三点到平面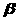 的距离相等,则
的距离相等,则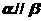 ;(4)若直线
;(4)若直线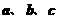 满足
满足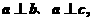 则
则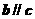 .其中正确命题的个数是
( )
.其中正确命题的个数是
( )
A. 个
B.
个
B.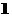 个
C.
个
C.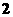 个 D.
个 D.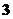 个
个
5 设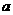 、
、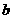 为两条直线,
为两条直线,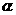 、
、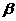 为两个平面. 下列四个命题中,正确的命题是 ( )
为两个平面. 下列四个命题中,正确的命题是 ( )
A. 若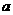 、
、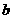 与
与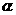 所成的角相等,则
所成的角相等,则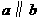 ; B. 若
; B. 若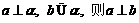 ;
;
C. 若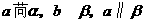 ,则
,则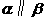 ; D. 若
; D. 若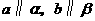 ,
,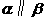 ,则
,则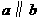 .
.
6已知长方体的表面积是 ,过同一顶点的三条棱长之和是
,过同一顶点的三条棱长之和是 ,则它的对角线长是( )
,则它的对角线长是( )
A.  B.
B.
 C.
C.
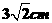 D.
D.

7在底面为正方形的长方体上任意选择4个顶点,它们可能是如下各种几何形体的4个顶点,①矩形;②不是矩形的平行四边形;③有三个面为直角三角形,有一个面为等腰三角形的四面体;④每个面都是等腰三角形的四面体;⑤每个面都是直角三角形的四面体.
这些几何形体是( )
A.①②④⑤ B.①②③⑤ C.①②③④ D.①③④⑤
8已知圆锥的母线长为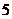
 ,侧面积为
,侧面积为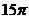
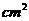 ,则此圆锥的体积为__________
,则此圆锥的体积为__________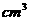 .
.
 9联结球面上任意两点的线段称为球的弦,已知半径为
9联结球面上任意两点的线段称为球的弦,已知半径为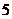 的球上有两条长分别为
的球上有两条长分别为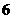 和
和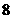 的弦,则此两弦中点距离的最大值是____________.
的弦,则此两弦中点距离的最大值是____________.
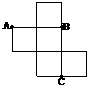
10
如图,是一个无盖正方体盒子的表面展开图, 为其上
为其上
的三个点,则在正方体盒子中, ____________.
____________.
11若圆锥的侧面积为 ,且母线与底面所成的角为
,且母线与底面所成的角为 ,则该圆锥的体积为_______
,则该圆锥的体积为_______
12若取地球的半径为 米,球面上两点
米,球面上两点 位于东经
位于东经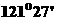 ,北纬
,北纬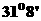 ,
,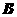 位于东经
位于东经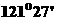 ,北纬
,北纬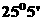 ,则
,则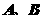 两点的球面距离为_____________千米(精确到1千米).
两点的球面距离为_____________千米(精确到1千米).
13已知某铅球的表面积是 ,则该铅球的体积是___________
,则该铅球的体积是___________ .
.
14已知圆锥的母线长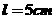 ,高
,高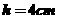 ,则该圆锥的体积是____________
,则该圆锥的体积是____________
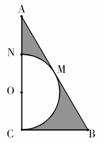 15
如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是 .
15
如图,圆锥的侧面展开图恰好是一个半圆,则该圆锥的母线与底面所成的角的大小是 .
16如图,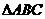 中,
中,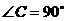 ,
,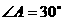 ,
,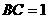 .在三角形内挖去半圆
.在三角形内挖去半圆
(圆心O在边AC上,半圆与BC、AB相切于点C、M,与AC交于N),则图
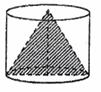 中阴影部分绕直线AC旋转一周所得旋转体的体积为
.
中阴影部分绕直线AC旋转一周所得旋转体的体积为
.
3.已知m、n为两条不同的直线,α、β为两个不同的平面,下列四个命题中,正确的是
( )
A.若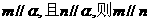 B.若
B.若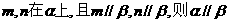
C.若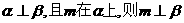 D.若
D.若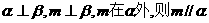
2.下列三个命题中错误的个数是 ( )
①经过球上任意两点,可以作且只可以作球的一个大圆;
②球的面积是它的大圆面积的四倍;
③球面上两点的球面距离,是这两点所在截面圆上以这两点为端点的劣弧的长.
A.0 B. 1 C. 2 D.3
1.设a,b,c表示三条直线,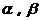 表示两个平面,下列命题中不正确的是---------(
)
表示两个平面,下列命题中不正确的是---------(
)
A.
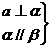
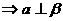 B.
B. 
C. 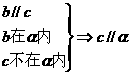 D.
D. 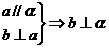
22、设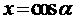
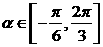 则
则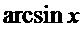 的取值范围
的取值范围
E、解斜三角形
23设△ABC的内角∠A、∠B、∠C所对的边长分别为a、b、c,且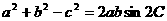 ,求角C的大小。
,求角C的大小。
24在 中,内角
中,内角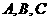 所对的边长分别是
所对的边长分别是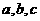 .
.
(Ⅰ)若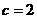 ,
,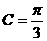 ,且
,且 的面积
的面积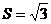 ,求
,求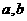 的值;
的值;
(Ⅱ)若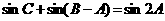 ,试判断
,试判断 的形状.
的形状.
25
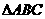 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为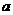 、
、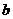 、
、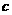 ,若
,若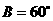 ,
, 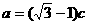 .
.
(1)求角 的大小;
的大小;
(2)已知当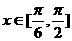 时,函数
时,函数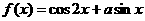 的最大值为3,求
的最大值为3,求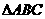 的面积.
的面积.
19、已知: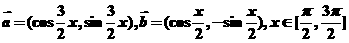 .
.
(1)求: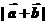 的取值范围;
的取值范围;
(2)求:函数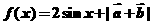 的最小值.
的最小值.
C、三角方程
20三角方程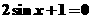 的解集是_____________.
的解集是_____________.
21方程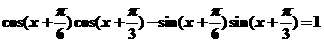 在
在 上的解集是____________.
上的解集是____________.
D、反三角函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com