
题目列表(包括答案和解析)
9.将一骰子向上抛掷两次,所得点数分别为 和
和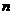 ,则函数
,则函数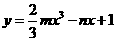 在
在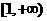 上为增函数的概率是( )
上为增函数的概率是( )

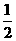
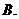
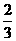

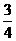
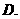
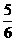
8.已知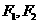 是双曲线
是双曲线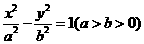 的两焦点,以线段
的两焦点,以线段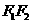 为边作正三角形
为边作正三角形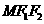 ,若边
,若边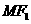 的中点在双曲线上,则双曲线的离心率是( )
的中点在双曲线上,则双曲线的离心率是( )

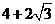
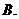
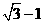

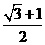
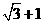
7.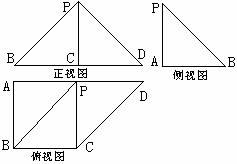 如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边
如图是一几何体的三视图,正视图是一等腰直角三角形,且斜边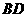 长为2;侧视图一直角三角形;俯视图为一直角梯形,且
长为2;侧视图一直角三角形;俯视图为一直角梯形,且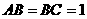 ,
,
则异面直线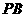 与
与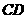 所成角的正切值是( )。
所成角的正切值是( )。

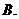
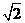

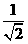
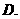
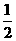
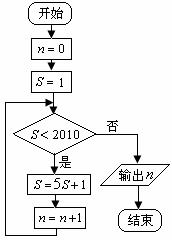
6.某程序框图如图所示,该程序运行后输出的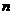 值是( )
值是( )


5.在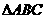 中,设
中,设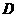 是
是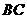 边上的一点,且满足
边上的一点,且满足
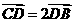 ,
,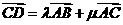 ,则
,则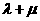 的值为( )
的值为( )

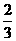
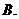
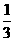

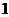

4.已知函数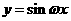 在
在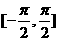 内是减函数, 则( )
内是减函数, 则( )


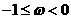

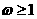
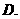
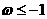
3. 设复数z满足关系
设复数z满足关系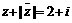 ,那么z等于( ).
,那么z等于( ).

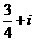
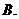
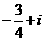

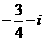
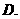
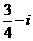
2.若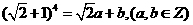 ,则
,则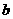 的值为( )
的值为( )

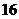
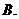
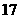

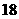
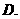
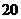
1.已知集合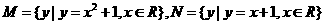 ,则
,则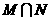 =( )
=( )

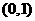 ,
,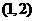
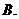
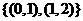

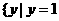 或
或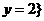
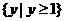
20、已知椭圆中心在原点,焦点在y轴上,离心率为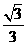 ,以原点为圆心,椭圆短半轴长为半径的圆与直线
,以原点为圆心,椭圆短半轴长为半径的圆与直线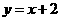 相切.
相切.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)设点F是椭圆在y轴正半轴上的一个焦点,点A,B是抛物线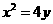 上的两个动点,且满足
上的两个动点,且满足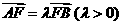 ,过点A,B分别作抛物线的两条切线,设两切线的交点为M,试推断
,过点A,B分别作抛物线的两条切线,设两切线的交点为M,试推断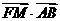 是否为定值?若是,求出这个定值;若不是,说明理由.
是否为定值?若是,求出这个定值;若不是,说明理由.
[解](Ⅰ)设椭圆方程为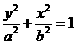 (a>b>0).
(1分)
(a>b>0).
(1分)
因为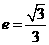 ,得
,得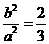 .又
.又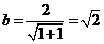 ,则
,则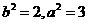 .
.
故椭圆的标准方程是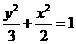 .
(5分)
.
(5分)
(Ⅱ)由椭圆方程知,c=1,所以焦点F(0,1),设点A(x1,y1),B(x2,y2). (6分)
由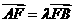 ,得(-x1,1-y1)=λ(x2,y2-1),所以-x1=λx2,1-y1=λ(y2-1). (7分)
,得(-x1,1-y1)=λ(x2,y2-1),所以-x1=λx2,1-y1=λ(y2-1). (7分)
于是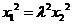 .因为
.因为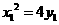 ,
,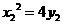 ,则y1=λ2y2.
,则y1=λ2y2.
联立y1=λ2y2和1-y1=λ(y2-1),得y1=λ,y2=. (8分)
因为抛物线方程为y=x2,求导得y′=x.设过抛物线上的点A、B的切线分别为l1,l2,则
直线l1的方程是y=x1(x-x1)+y1,即y=x1x-x12. (9分)
直线l2的方程是y=x2(x-x2)+y2,即y=x2x-x22. (10分)
联立l1和l2的方程解得交点M的坐标为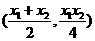 .
(11分)
.
(11分)
因为x1x2=-λx22=-4λy2=-4. 所以点M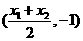 . (12分)
. (12分)
于是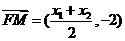 ,
,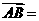 (x2-x1,y2-y1).
(x2-x1,y2-y1).
所以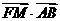 =
=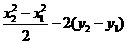 =(x22-x12)-2(x22-x12)=0.
=(x22-x12)-2(x22-x12)=0.
故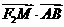 为定值0.
(13分)
为定值0.
(13分)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com