
题目列表(包括答案和解析)
19. (本小题满分12分)
在数列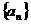 中,
中,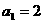 ,
,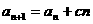 (
(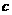 是常数,
是常数,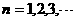 ),且
),且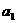 ,
,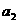 ,
,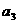 成公比不为
成公比不为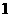 的等比数列.
的等比数列.
(1)求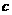 的值;
的值;
(2)求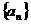 的通项公式.
的通项公式.
18. (本小题满分12分)
(本小题满分12分)
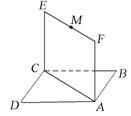
如图,已知正方形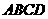 和矩形
和矩形 所在的平面互相垂直,
所在的平面互相垂直,
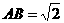 ,
,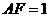 ,
,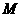 是线段
是线段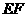 的中点.
的中点.
(1)求证 ∥平面
∥平面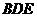 ;
;
(2)试在线段 上确定一点
上确定一点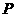 ,使得
,使得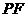 与
与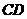 所成的角是
所成的角是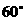 .
.
17.(本小题满分12分)
已知向量a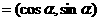 ,b
,b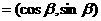 ,∣a–b∣
,∣a–b∣ 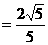 .
.
(1)求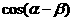 的值;
的值;
(2)若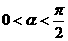 ,
,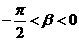 , 且
, 且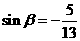 , 求
, 求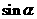 .
.
22.解:(1)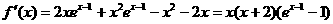 …………2分
…………2分
令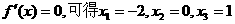
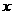 |
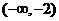 |
-2 |
(-2,0) |
0 |
(0,1) |
1 |
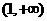 |
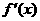 |
- |
0 |
+ |
0 |
- |
0 |
+ |
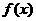 |
减 |
极小 |
增 |
极大 |
减 |
极小 |
增 |
函数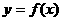 的增区间为
的增区间为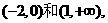
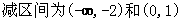 …………5分
…………5分
(2)当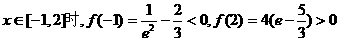
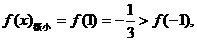
所以 ………………8分
………………8分
(3)设
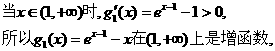
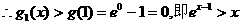 ; ………………10分
; ………………10分

即当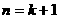 时,不等式成立。
时,不等式成立。
所以当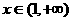 时,
时,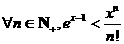 ………………14分
………………14分
[2010烟台一模]
21.解:(1)由题设点C到点F的距离等于它到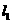 的距离,
的距离,
∴点C的轨迹是以F为焦点,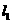 为准线的抛物线 ………………2分
为准线的抛物线 ………………2分
∴所求轨迹的方程为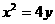 ………………4分
………………4分
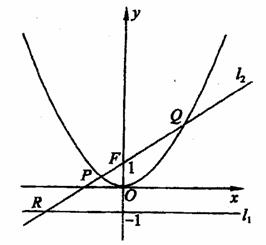
(2)由题意直线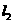 的方程为
的方程为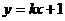 ,
,
与抛物线方程联立消去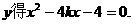
记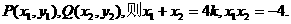 ………………6分
………………6分
因为直线PQ的斜率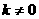 ,易得点R的坐标为
,易得点R的坐标为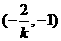
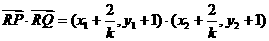
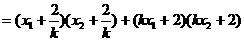 ………………8分
………………8分
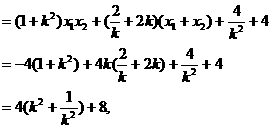
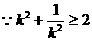 ,当且仅当
,当且仅当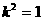 时取到等号。 ………………11分
时取到等号。 ………………11分
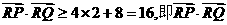 的最小值为16 ………………12分
的最小值为16 ………………12分
20.解:(1)分别记“客人游览大明湖景点”,“客人游览趵突泉景点”,“客人游览千佛山景点”,“客人游览园博园景点”为事件A1,A2,A3,A4。
由已知A1,A2,A3,A4相互独立,
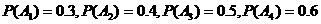 ………………2分
………………2分
客人游览景点数的可能取值为0。1,2,3,4。相应地,客人没有游览的景点数的可能取值为4,3,2,1,0,所以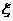 的可能取值为0,2,4。 ………………3分
的可能取值为0,2,4。 ………………3分
故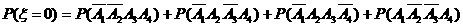
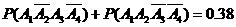 ………………6分
………………6分
(2)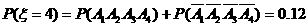 ………………8分
………………8分
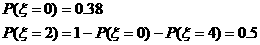
所以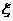 的分布列为
的分布列为
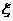 |
0 |
2 |
4 |
|
P |
0.38 |
0.5 |
0.12 |
………………10分
E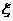 =1.48. ……………………………………………………12分
=1.48. ……………………………………………………12分
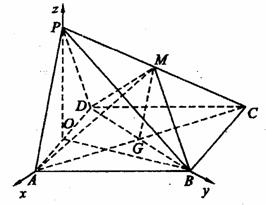
19.解:(1)证明:连接AC,AC与BD交于G,则面PAC∩面BDM=MG,
由PA//平面BDM,可得PA//MG ………………3分
∵底面ABCD为菱形,∴G为AC的中点,
∴MG为△PAC的中位线。
因此M为PC的中点。 ………………5分
(2)取AD中点O,连结PO,BO。
∵△PAD是正三角形,∴PO⊥AD,又因为平面PAD⊥平面ABCD,
所以,PO⊥平面ABCD, ………………7分
∵底面ABCD是菱形且∠BAD=60°,△ABD是正三角形,
∴AD⊥OB。
∴OA,OB,OP两两垂直,建立空间直角坐标系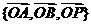 …………7分
…………7分
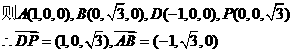
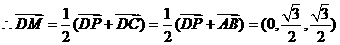 ………………9分
………………9分
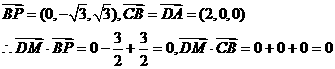
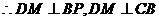 ………………11分
………………11分
∴DM⊥平面PBC,又DM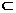 平面ADM,
平面ADM,
∴ADM⊥面PBC ………………12分
注:其他方法参照给分。
18.解:(1)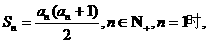
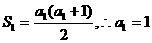 …………1分
…………1分
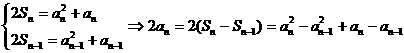 …………3分
…………3分
所以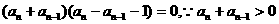
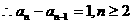 ,所以数列
,所以数列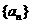 是等差数列 ………………6分
是等差数列 ………………6分
(2)由(1)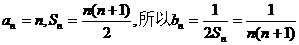 ………………8分
………………8分
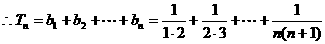
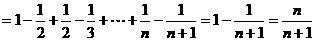 …………12分
…………12分
17.解:(1)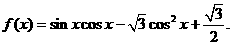 ………………2分
………………2分
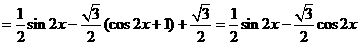
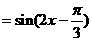 ………………4分
………………4分
所以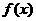 的最小正周期为
的最小正周期为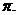 ………………5分
………………5分
令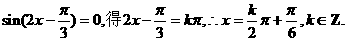
故所求对称中心的坐标为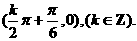 ………………8分
………………8分
(2)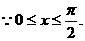
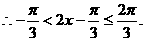 ………………10分
………………10分
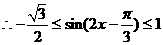
即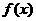 的值域为
的值域为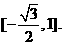 ………………12分
………………12分
22.(本题满分14分)
设函数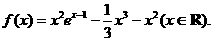
(1)求函数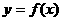 的单调区间;
的单调区间;
(2)求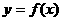 在[-1,2]上的最小值;
在[-1,2]上的最小值;
(3)当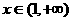 时,用数学归纳法证明:
时,用数学归纳法证明: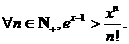
[2010济南一模]答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com