
题目列表(包括答案和解析)
4.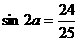 ,
,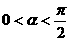 ,则
,则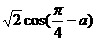 的值为( )
的值为( )
A.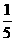 B.
B.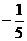 C.
C.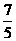 D.
D.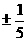
3.设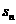 是等差数列{
是等差数列{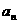 }的前n项和,已知
}的前n项和,已知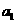 =3,
=3,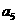 =11,则
=11,则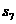 等于( )
等于( )
A.13 B.35 C.49 D.63
2.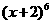 的展开式中
的展开式中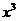 的系数为( )
的系数为( )
A.20 B.40 C.80 D.160
1.复数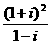 等于( )
等于( )
A.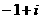 B.
B.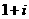 C.
C.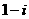 D.
D.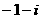
22.解:(Ⅰ) 函数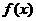 的导函数
的导函数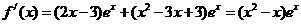 ,欲使得函数
,欲使得函数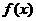 在
在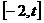 上为单调函数,因当
上为单调函数,因当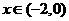 时,
时,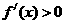 ,当
,当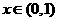 时,
时,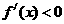 ,故只要
,故只要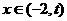 时,
时,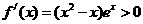 恒成立,可得
恒成立,可得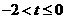 。…
。…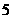 分
分
(Ⅱ)当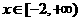 时,
时,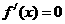 得
得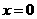 或
或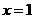 ,又
,又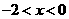 时,
时,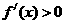 ,
,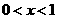 时,
时,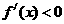 ,
,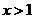 时,
时,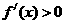 ,所以
,所以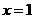 时,
时,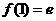 是函数
是函数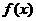 在
在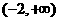 上的极小值,
上的极小值,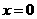 时,
时,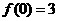 是函数
是函数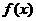 在
在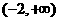 上的极大值,当
上的极大值,当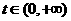 时,有
时,有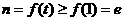 ,而
,而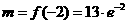 ,由
,由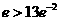 知
知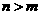 ,
,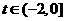 时由单调性知
时由单调性知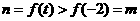 。…
。…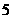 分
分
(Ⅲ) 对于任意的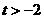 ,
,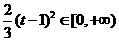 ,而
,而
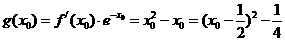
⑴当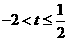 时,
时,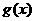 在
在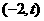 上单调递减,只要证
上单调递减,只要证
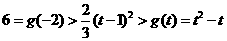 ,
,
即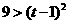 且
且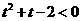 ①,由
①,由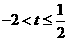 知①显然成立,且
知①显然成立,且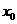 有唯一解。……
有唯一解。…… 分
分
⑵当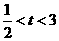 时,只要证
时,只要证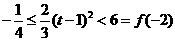 ,只要证
,只要证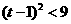 ,显然成立。
,显然成立。
当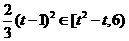 ,即
,即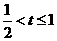 时,
时,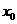 一解,当
一解,当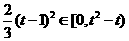 即
即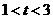 时,
时,
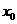 二解
二解
⑶当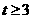 时,只要证
时,只要证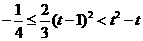 ,
,
即证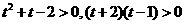 ,显然成立。
,显然成立。
当时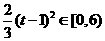 ,即
,即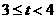 时,
时,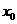 二解,当
二解,当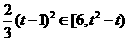 ,即
,即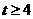 ,
,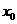 一解。
一解。
综合以上,当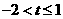 或
或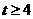 时,
时,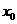 一解;当
一解;当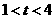 时,
时,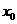 二解。……
二解。…… 分。
分。
22.(本题满分15分)已知函数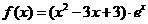 定义域为
定义域为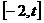 (
(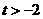 ),设
),设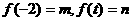 .
.
(Ⅰ)试确定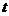 的取值范围,使得函数
的取值范围,使得函数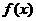 在
在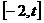 上为单调函数;
上为单调函数;
(Ⅱ)求证: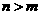 ;
;
(Ⅲ)求证:对于任意的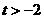 ,总存在
,总存在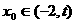 ,满足
,满足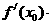
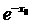
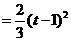 ,并确定这样的
,并确定这样的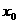 的个数 (其中
的个数 (其中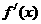 为函数
为函数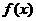 的导函数) .
的导函数) .
21.解:(Ⅰ)证明(略),定点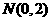 ……
…… 分
分
(Ⅱ)设点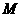 坐标为
坐标为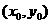 ,则
,则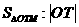 =
=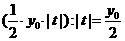 ,由(Ⅰ)直线
,由(Ⅰ)直线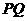 过定点
过定点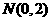 ,设直线
,设直线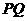 方程为
方程为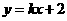 代入
代入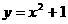 整理得
整理得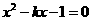 ,设
,设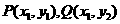 ,
,
则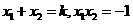 ,
,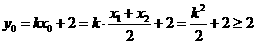 ,当
,当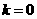 时,
时,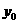 最小值为
最小值为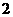 ,所以
,所以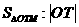 最小值为
最小值为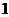 。……
。…… 分
分
21.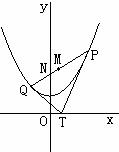 (本题满分15分)过
(本题满分15分)过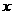 轴上的动点
轴上的动点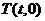 ,引抛物线
,引抛物线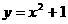 两条切线
两条切线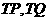 ,
,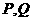 为切点。
为切点。
(Ⅰ)求证:直线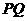 过定点
过定点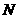 ,并求出定点
,并求出定点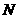 坐标;
坐标;
(Ⅱ)若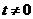 ,设弦
,设弦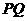 的中点为
的中点为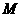 ,试求
,试求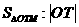 的最小值(
的最小值( 为坐标原点).
为坐标原点).
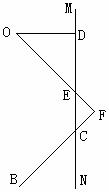
20.解:(Ⅰ)如图,作 ⊥
⊥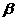 于
于 ,
,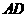 ⊥
⊥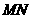 于
于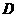 ,连接
,连接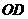 ,知
,知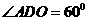 ,在
,在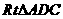 中,易得
中,易得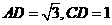 ,在
,在 中,
中,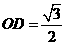 ,
,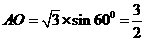 ……7分。
……7分。
(Ⅱ)如图,在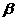 平面内,过点
平面内,过点 作直线
作直线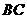 的垂线,垂足为
的垂线,垂足为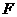 ,与直线
,与直线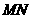 交于
交于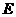 点,易证
点,易证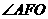 为二面角
为二面角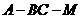 的平面角,由已知得
的平面角,由已知得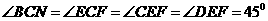 ,可求得
,可求得
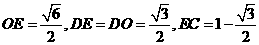 ,
,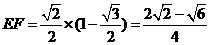 ,
,
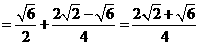 ,
,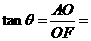
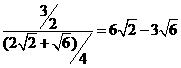 ……
…… 分
分
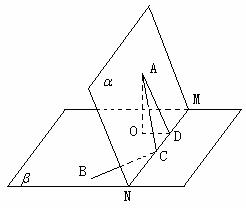
20.(本题满分14分)如图,已知平面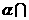 平面
平面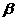 =
=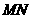 ,
,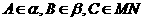 ,且
,且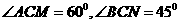 ,二面角
,二面角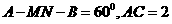 .
.
(Ⅰ)求点 到平面
到平面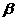 的距离;
的距离;
(Ⅱ)设二面角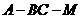 的大小为
的大小为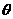 ,求
,求 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com