3、已知双曲线的两个焦点为F₁(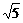－，0)、F₂(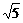，0)，P是此双曲线上的一点，且PF₁⊥PF₂，|PF₁|·|PF₂|=2，则该双曲线的方程是_____________________

2、已知A(0，7)、B(0，－7)、C(12，2)，以C为一个焦点作过A、B的椭圆，椭圆的另一个焦点F的轨迹方程是(　　 )

A.y²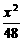－＝1(y≤－1) B.y²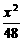－＝1 　　C.y²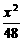－＝－1　　 　D.x²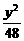－＝1

1、F₁、F₂为椭圆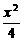+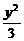=1的左、右焦点，A为椭圆上任一点，过焦点F₁向∠F₁AF₂的外角平分线作垂线，垂足为D，则点D的轨迹方程是________________.

2.在探求轨迹的过程中，需要注意的是轨迹的“完备性”和“纯粹性”，也就是说既不能多，也不能少，因此，在求得轨迹方程之后，要深入地再思考一下：①是否还遗漏了一些点？是否还有另一个满足条件的轨迹方程存在？②在所求得的轨迹方程中，x、y的取值范围是否有什么限制?

1.求动点轨迹方程常用的方法：

(1)直接法：如果题目中的条件有明显的等量关系，可用直接法. 其一般步骤是：建系、设点、列式、代入、化简、检验.检验就是要检验点的轨迹的纯粹性和完备性.

(2)定义法：如果能够确定动点的轨迹满足某种已知曲线的定义，则可用曲线定义写出方程，是从常见曲线的定义出发寻找解决问题的方法.

(3)几何法：利用几何性质，若所求的轨迹与图形的性质相关，往往利用三角形或圆的性质来解问题；

(4)代入法：如果轨迹动点P(x，y)依赖于另一动点Q(a，b)，而Q(a，b)又在某已知曲线上，则可先列出关于x、y、a、b的方程组，利用x、y表示出a、b，把a、b代入已知曲线方程便得动点P的轨迹方程.此法称为代入法.

(5)参数法：.如果轨迹动点P(x，y)的坐标之间的关系不易找到，也没有相关点可用时，可先考虑将x、y用一个或几个参数来表示，消去参数得轨迹方程，此法称为参数法.参数常选角、斜率等.

18、若点(1,1)到直线xcosα+ysinα＝2的距离为d，则d的最大值是　　　　 ．

B、轨迹问题

17、圆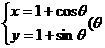为参数)的标准方程是　　　　　　　 ，过这个圆外一点P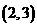的该圆的切线方程是　　　　　　　　　　　 。

16、光线从点P(－3，5)射到直线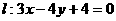上，经过反射，其反射光线过点Q(3，5)，则光线从P到Q所走过的路程为　　　　　　　 .

15、直线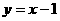上的点到圆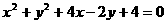上的点的最近距离是___________　 　

14、m＝－1是直线mx+(2m－1)y+1＝0和直线3x+my+3＝0垂直的_____________条件