
题目列表(包括答案和解析)
75. 设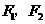 分别是双曲线
分别是双曲线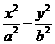 的左、右焦点,若双曲线上存在点
的左、右焦点,若双曲线上存在点 ,使
,使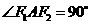 且
且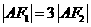 ,则双曲线的离心率为
,则双曲线的离心率为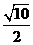
76 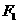 和
和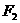 分别是双曲线
分别是双曲线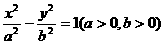 的左、右焦点,
的左、右焦点, 和
和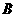 是以
是以 为圆心,以
为圆心,以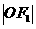 为半径的圆与该双曲线左支的两个交点,且△
为半径的圆与该双曲线左支的两个交点,且△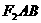 是等边三角形,则双曲线的离心率为
是等边三角形,则双曲线的离心率为 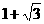 .
.
77 双曲线虚轴上的一个端点为M,两个焦点为F1 F2,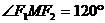 ,则双曲线的离心率为
,则双曲线的离心率为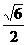
71.在给定椭圆中,过焦点且垂直于长轴的弦长为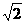 ,焦点到相应准线的距离为1,则该椭圆的离心率为解:不妨设椭圆方程为
,焦点到相应准线的距离为1,则该椭圆的离心率为解:不妨设椭圆方程为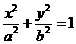 (a>b>0),则有
(a>b>0),则有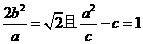 ,据此求出e=
,据此求出e=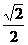 ,
,
72已知椭圆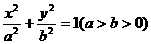 ,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线
,它的上下顶点分别是A、B,点M是椭圆上的动点(不与A、B重合),直线AM交直线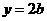 于点N,且
于点N,且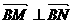 .
.
(1)求椭圆的离心率;
(2)若斜率为1的直线l交椭圆于P、Q两点,求证: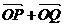 与向量
与向量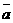 =(-3,1)共线(其中O为坐标原点)
=(-3,1)共线(其中O为坐标原点)
解:(1)设M(x0,y0),又点A(0,b),B(0,-b)
∴直线AM: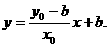
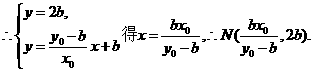
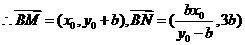
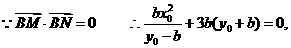
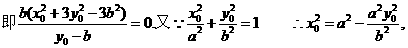
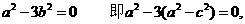
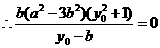
解得: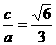 ,即离心率
,即离心率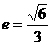 .
.
(2)设直线l: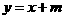
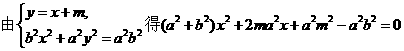
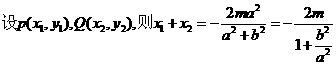
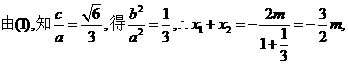
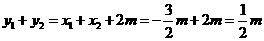
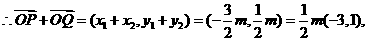
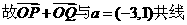
73已知双曲线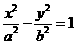
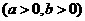 的左、右焦点分别为F1、F2,P是准线上一点,且P F1⊥P F2,|P
F1|
的左、右焦点分别为F1、F2,P是准线上一点,且P F1⊥P F2,|P
F1|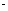 |P F2 |=4ab,则双曲线的离心率是
|P F2 |=4ab,则双曲线的离心率是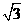
74 设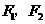 分别是椭圆
分别是椭圆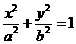 (
(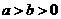 )的左、右焦点,若在其右准线上存在
)的左、右焦点,若在其右准线上存在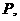 使线段
使线段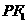 的中垂线过点
的中垂线过点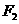 ,则椭圆离心率的取值范围是
,则椭圆离心率的取值范围是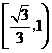
65.椭圆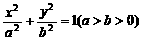 的两个焦点是F1、F2,以| F1F2
|为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为_
的两个焦点是F1、F2,以| F1F2
|为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为_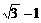 ___________。
___________。
66设椭圆的两个焦点分别为F1、、F2,过F2作椭圆长轴的垂线交椭圆于点P,若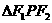 为
为
等腰直角三角形,则椭圆的离心率是__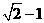 __________。
__________。
67已知双曲线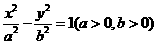 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为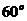 的直线与
的直线与
双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是___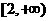 _________。
_________。
68已知椭圆E的离心率为e,两焦点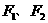 ,抛物线c以
,抛物线c以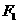 为顶点、以
为顶点、以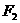 为焦点,P为两曲线的一个交点,若
为焦点,P为两曲线的一个交点,若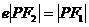 ,则离心率
,则离心率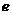 的值为__
的值为__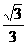 _______.
_______.
69双曲线虚轴上的一个端点为M,两个焦点为F1、F2,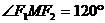 ,则双曲线的离心率为
,则双曲线的离心率为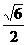
70已知双曲线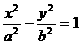 (a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
(a>0,b<0)的右焦点为F,若过点F且倾斜角为60°的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
解析:双曲线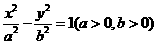 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为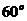 的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率
的直线与双曲线的右支有且只有一个交点,则该直线的斜率的绝对值小于等于渐近线的斜率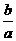 ,∴
,∴ 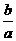 ≥
≥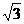 ,离心率e2=
,离心率e2=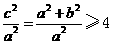 ,∴ e≥2,
,∴ e≥2,
27、如果以原点为圆心的圆经过双曲线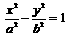 的焦点,并且被该双曲线的右准线分为弧长为2:1的两段圆弧,那么该双曲线的离心率为
的焦点,并且被该双曲线的右准线分为弧长为2:1的两段圆弧,那么该双曲线的离心率为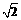
28已知双曲线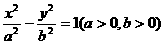 的左、右焦点分别为F1,F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为 1<e≤2
的左、右焦点分别为F1,F2,若在双曲线的右支上存在一点P,使得|PF1|=3|PF2|,则双曲线的离心率e的取值范围为 1<e≤2
29已知椭圆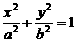 的左、右焦点分别为F1,F2,点P为椭圆上一点,且∠PF1F2=30°,∠PF2F1=60°,则椭圆的离心率e= -1
的左、右焦点分别为F1,F2,点P为椭圆上一点,且∠PF1F2=30°,∠PF2F1=60°,则椭圆的离心率e= -1
30过双曲线M: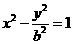 的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C两点 , 且
的左顶点A作斜率为1的直线l,若l与双曲线M的两条渐近线相交于B、C两点 , 且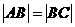 , 则双曲线M的离心率为_
, 则双曲线M的离心率为_
31与双曲线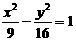 有共同的渐近线,且焦点在y轴上的双曲线的离心率为
有共同的渐近线,且焦点在y轴上的双曲线的离心率为 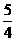
32若双曲线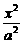 -
-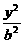 =1的渐近线与方程为
=1的渐近线与方程为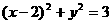 的圆相切,则此双曲线的离心率为 2
的圆相切,则此双曲线的离心率为 2
33点P是双曲线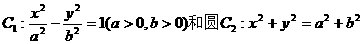 的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为
的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为 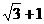
34已知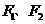 分别为双曲线
分别为双曲线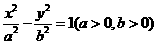 的左右焦点,
的左右焦点,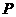 为双曲线左支上的一点,若
为双曲线左支上的一点,若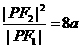 ,则双曲线的离心率的取值范围是(1,3]
,则双曲线的离心率的取值范围是(1,3]
35若椭圆的焦距长等于它的短轴长,则椭圆的离心率等于_
36已知双曲线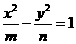 的一条渐近线方程为
的一条渐近线方程为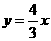 ,则该双曲线的离心率
,则该双曲线的离心率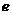 为
为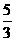 或
或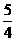
37点P是双曲线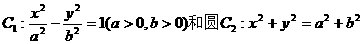 的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为 +1
的一个交点,且2∠PF1F2=∠PF2F1,其中F1、F2是双曲线C1的两个焦点,则双曲线C1的离心率为 +1
38已知椭圆E的短轴长为6,焦点F到长轴的一个端点的距离等于9,则椭圆E的离心率等于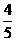
39从一块短轴长为2b的椭圆形玻璃镜中划出一块面积最大的矩形,其面积的取值范围是[3b2,4b2],则这一椭圆离心率e的取值范围是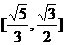
39已知点A, F分别是椭圆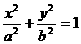 (a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若
(a>b>0)的右顶点和左焦点,点B为椭圆短轴的一个端点,若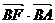 =0,则椭圆的离心率e为
=0,则椭圆的离心率e为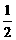 (
(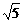 -1)
-1)
40以椭圆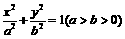 的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为
的右焦点为圆心的圆经过原点,且被椭圆的右准线分成弧长为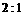 的两段弧,那么该椭圆的离心率等于
的两段弧,那么该椭圆的离心率等于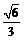
41已知双曲线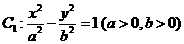 的左、右焦点分别为
的左、右焦点分别为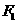 、
、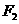 ,抛物线
,抛物线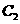 的顶点在原点,它的准线与双曲线
的顶点在原点,它的准线与双曲线 的左准线重合,若双曲线
的左准线重合,若双曲线 与抛物线
与抛物线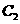 的交点
的交点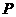 满足
满足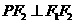 ,则双曲线
,则双曲线 的离心率为
的离心率为
42椭圆的长轴为A1A2,B为短轴一端点,若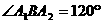 ,则椭圆的离心率为
,则椭圆的离心率为
43已知点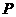 是以
是以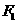 、
、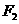 为焦点的椭圆
为焦点的椭圆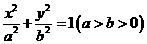 上的一点,若
上的一点,若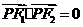 ,
,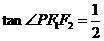 ,则此椭圆的离心率为
,则此椭圆的离心率为
44ABCDEF为正六边形,则以F、C为焦点,且经过A、E、D、B四点的双曲线的离心率为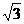 +1
+1
45两个正数a、b的等差中项是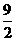 ,一个等比中项是
,一个等比中项是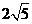 ,且
,且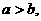 则双曲线
则双曲线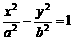 的离心率为解析:由已知得
的离心率为解析:由已知得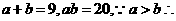
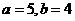 ,
,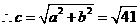 ,
,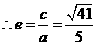 ,
,
46已知点F是双曲线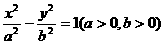 的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是(1,2)
的左焦点,点E是该双曲线的右顶点,过F且垂直于x轴的直线与双曲线交于A、B两点,若△ABE是锐角三角形,则该双曲线的离心率e的取值范围是(1,2)
47已知双曲线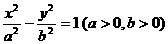 ,被方向向量为
,被方向向量为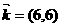 的直线截得的弦的中点为(4,1),则该双曲线离心率的值是
的直线截得的弦的中点为(4,1),则该双曲线离心率的值是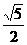
48已知双曲线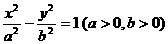 ,被方向向量为
,被方向向量为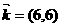 的直线截得的弦的中点为(4,1),则该双曲线离心率的值是
的直线截得的弦的中点为(4,1),则该双曲线离心率的值是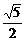
49已知双曲线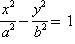 (a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是(1,
(a>0,b>0),若过右焦点F且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是(1,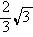 )
)
50过双曲线M: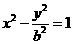
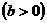 的左顶点A作斜率为1的直线
的左顶点A作斜率为1的直线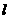 ,若
,若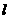 与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是(
与双曲线M的两条渐近线分别相交于B、C,且|AB|=|BC|,则双曲线M的离心率是(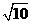 )
)
51设双曲线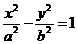 (b>a>0)的半焦距为c,直线l过A(a,0),B(0,b)两点,若原点O到l的距离为
(b>a>0)的半焦距为c,直线l过A(a,0),B(0,b)两点,若原点O到l的距离为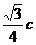 ,则双曲线的离心率为2
,则双曲线的离心率为2
52双曲线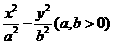 的左、右焦点分别为F1、F2,过焦点F2且垂直于x轴的弦为AB,若
的左、右焦点分别为F1、F2,过焦点F2且垂直于x轴的弦为AB,若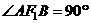 ,则双曲线的离心率为
,则双曲线的离心率为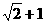 ( )
( )
58已知双曲线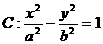 的焦点为
的焦点为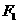 、
、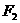 ,
,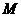 为双曲线上一点,以
为双曲线上一点,以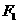
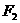 为直径的圆与双曲线的一个交点为
为直径的圆与双曲线的一个交点为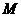 ,且
,且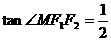 ,则双曲线的离心率为
,则双曲线的离心率为
59设斜率为2的直线l,过双曲线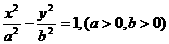 的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率,e的取值范围是e>
的右焦 点,且与双曲线的左、右两支分别相交,则双曲线离心率,e的取值范围是e>
60若直线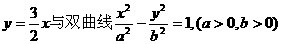 的交点在实轴上射影恰好为双曲线的焦点,则双曲线的离心率是2
的交点在实轴上射影恰好为双曲线的焦点,则双曲线的离心率是2
61已知双曲线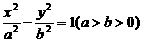 的离心率是,则椭圆
的离心率是,则椭圆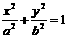 的离心率是
的离心率是
62已知点F1,F2分别是双曲线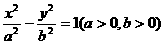 的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是
的左、右焦点,过F1且垂直于x轴的直线与双曲线交于A,B两点,若△ABF2是锐用三角形,则该双曲线离心率的取值范围是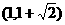
63已知椭圆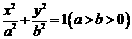 与双曲线
与双曲线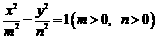 有相同的焦点
有相同的焦点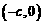 和
和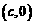 ,若
,若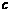 是
是 的等比中项,
的等比中项,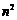 是
是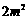 与
与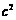 的等差中项,则椭圆的离心率是
的等差中项,则椭圆的离心率是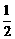
64椭圆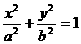
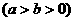 的离心率为
的离心率为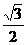 ,则双曲线
,则双曲线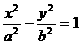 的离心率为_
的离心率为_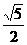
24.已知双曲线的顶点到渐近线的距离为2,焦点到渐近线的距离为6,则该双曲线的离心率为 3 .
25已知双曲线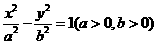 的右焦点为F,若过点F且倾斜角的
的右焦点为F,若过点F且倾斜角的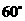 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是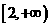
26在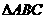 中,
中,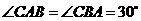 。AC、BC边上的高分别为BD、AE,则以A、B为焦点且过D、E的椭圆与双曲线的离心率的倒数和为
。AC、BC边上的高分别为BD、AE,则以A、B为焦点且过D、E的椭圆与双曲线的离心率的倒数和为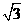
22.已知椭圆E: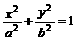 (a>b>0),以F1(-c,0)为圆心,以a-c为半径作圆F1,过点B2(0,b)作圆F1的两条切线,设切点为M、N.
(a>b>0),以F1(-c,0)为圆心,以a-c为半径作圆F1,过点B2(0,b)作圆F1的两条切线,设切点为M、N.
(1)若过两个切点M、N的直线恰好经过点B1(0,-b)时,求此椭圆的离心率;
(2)若直线MN的斜率为-1,且原点到直线MN的距离为4(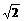 -1),求此时的椭圆方程;
-1),求此时的椭圆方程;
(3)是否存在椭圆E,使得直线MN的斜率k在区间(-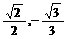 )内取值?若存在,求出椭圆E的离心率e的取值范围;若不存在,请说明理由.
)内取值?若存在,求出椭圆E的离心率e的取值范围;若不存在,请说明理由.
解:(1)圆F1的方程是(x+c)2+y2=(a-c)2,因为B2M、B2N与该圆切于M、N点,所以B2、M、F1、N四点共圆,且B2F1为直径,则过此四点的圆的方程是(x+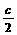 )2+(y-
)2+(y-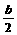 )2=
)2=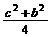 ,从而两个圆的公共弦MN的方程为cx+by+c2=(a-c)2,又点B1在MN上,
,从而两个圆的公共弦MN的方程为cx+by+c2=(a-c)2,又点B1在MN上,
∴a2+b2-2ac=0,∵b2=a2-c2,
∴2a2-2ac-c2=0,即e2+2e-2=0,∴e=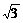 -1.(负值已舍去)
-1.(负值已舍去)
(2)由(1)知,MN的方程为cx+by+c2=(a-c)2,由已知-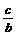 =-1.
=-1.
∴b=c,而原点到MN的距离为d=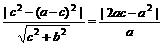 =|2c-a|=
=|2c-a|=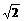 a,
a,
∴a=4,b2=c2=8,所求椭圆方程是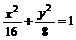 ;
;
(3)假设这样的椭圆存在,由(2)则有-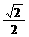 <-
<-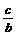 <-
<-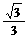 ,
,
∴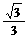 <
<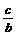 <
<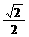 ,∴
,∴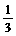 <
<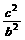 <
<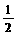 ,∴
,∴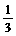 <
<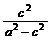 <
<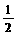 .故得2<
.故得2<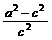 <3,
<3,
∴3<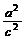 <4,求得
<4,求得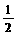 <e<
<e<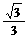 ,即当离心率取值范围是(
,即当离心率取值范围是(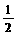 ,
,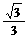 )时,直线MN的斜率可以在区间?(
)时,直线MN的斜率可以在区间?(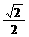 ,-
,-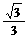 )内取值.
)内取值.
23 过双曲线的一个焦点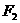 作垂直于实轴的直线,交双曲线于P、Q,
作垂直于实轴的直线,交双曲线于P、Q,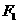 是另一焦点,若∠
是另一焦点,若∠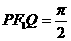 ,则双曲线的离心率
,则双曲线的离心率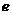 等于
等于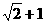
21. 如果正△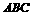 中,
中,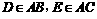 ,向量
,向量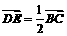 ,那么以
,那么以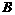 ,
,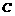 为焦点且过点
为焦点且过点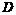 ,
,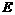 的双曲线的离心率是
的双曲线的离心率是 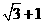 .
.
20.点P(-3,1)在椭圆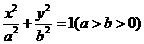 的左准线上,过点P且方向向量为
的左准线上,过点P且方向向量为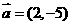 的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为
的光线,经直线y=-2反射后通过椭圆的左焦点,则这个椭圆的离心率为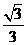
19. 已知双曲线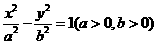 的右焦点为F,若过点F且倾斜角为
的右焦点为F,若过点F且倾斜角为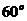 的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是
的直线与双曲线的右支有且只有一个交点,则此双曲线离心率的取值范围是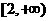
18.椭圆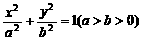 的两个焦点是F1、F2,以| F1F2
|为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为
的两个焦点是F1、F2,以| F1F2
|为边作正三角形,若椭圆恰好平分三角形的另两边,则椭圆的离心率为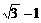
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com