6．共有10项的数列{a_n}的通项a_n＝，则该数列中最大项、最小项的情况是

(　)

A．最大项为a₁，最小项为a₁₀　 　　　　　　　　　 B．最大项为a₁₀，最小项为a₁

C．最大项为a₆，最小项为a₅　 　　　　　　　　　 D．最大项为a₄，最小项为a₃

解析：a_n＝＝1+，则a_n在n≤3且n∈N^*时为递减数列，n≥4，n∈N^*时也为递减数列，

∴1>a₁>a₂>a₃，a₄>a₅>a₆>…>a₁₀>1.

故最大项为a₄，最小项为a₃.

答案：D

5．已知a₁＝1，a_n＝n(a_n+1－a_n)(n∈N^*)，则数列{a_n}的通项公式是(　)

A．2n－1　 　　　　　　　　　　　 B．()^n－1

C．n²　 　　　　　　　　　　　　　　 D．n

解析：法一：由已知整理得(n+1)a_n＝na_n+1，

∴＝，∴数列{}是常数列．

且＝＝1，∴a_n＝n.

法二：累乘法：n≥2时，＝

＝

⋮

＝

＝

两边分别相乘得＝n.

又∵a₁＝1，∴a_n＝n.

答案：D

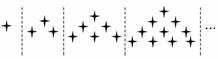
4．下列关于星星的图案构成一个数列，该数列的一个通项公式是(　)

A．a_n＝n²－n+1　 　　　　　　　　　 B．a_n＝

C．a_n＝　 　　　　　　　　　　　　　 D．a_n＝

解析：从图中可观察星星的构成规律，

n＝1时，有1个；n＝2时，有3个；

n＝3时，有6个；n＝4时，有10个；…

∴a_n＝1+2+3+4+…+n＝.

答案：C

3．下列说法正确的是(　)

A．数列1,3,5,7可表示为{1,3,5,7}

B．数列1,0，－1，－2与数列－2，－1,0,1是相同数列

C．数列{}的第k项为1+

D．数列0,2,4,6，…可记为{2n}

解析：由数列定义可知A、B错误；数列{}的第k项为＝1+，故C正确；数列0,2,4,6，…的通项公式为a_n＝2n－2，故D错．

答案：C

2．已知数列{a_n}满足a₁>0，＝，则数列{a_n}是(　)

A．递增数列　 　　　　　 B．递减数列

C．摆动数列　 　　　　　 D．不确定

解析：∵＝<1.又a₁>0，则a_n>0，∴a_n+1<a_n，

∴{a_n}是递减数列．

答案：B

1．在数列{a_n}中，a₁＝1，a_na_n－1＝a_n－1+(－1)ⁿ(n≥2，n∈N^*)，则的值是(　)

A.　　　　　B.

C.　 　　　　　　　　　　　　　　　　 D.

解析：由已知得a₂＝1+(－1)²＝2，

∴a₃·a₂＝a₂+(－1)³，∴a₃＝，

∴a₄＝+(－1)⁴，∴a₄＝3，

∴3a₅＝3+(－1)⁵，∴a₅＝，∴＝＝.

答案：C

8．在数列{a_n}中，若a₁＝1，a₂＝，＝+(n∈N^*)，则该数列的通项a_n＝________.

解析：由＝+，－＝－，

∴{}为等差数列．又＝1，d＝－＝1，

∴＝n，∴a_n＝.

7．已知数列{a_n}为等差数列，S_n为其前n项和，a₇－a₅＝4，a₁₁＝21，S_k＝9，则k＝________.

解析：a₇－a₅＝2d＝4，d＝2，a₁＝a₁₁－10d＝21－20＝1，

S_k＝k+×2＝k²＝9.又k∈N^*，故k＝3.

答案：3

6．已知数列{a_n}为等差数列，若<－1，且它们的前n项和S_n有最大值，则使S_n>0的n的最大值为(　)

A．11　 　　　　　　　　　　　 B．19

C．20　 　　　　　　　　　　　 D．21

解析：∵<－1，且S_n有最大值，

∴a₁₀>0，a₁₁<0，且a₁₀+a₁₁<0，

∴S₁₉＝＝19·a₁₀>0，

S₂₀＝＝10(a₁₀+a₁₁)<0，

所以使得S_n>0的n的最大值为19.

答案：B

5．已知等差数列{a_n}、{b_n}的公差分别为2和3，且b_n∈N^*，则数列{ab_n}是(　)

A．等差数列且公差为5　 　　　　　　　　　　 B．等差数列且公差为6

C．等差数列且公差为8　 　　　　　　　　　　 D．等差数列且公差为9

解析：依题意有ab_n＝a₁+(b_n－1)×2＝2b_n+a₁－2＝2b₁+2(n－1)×3+a₁－2＝6n+a₁+2b₁－8，故ab_n+1－ab_n＝6，即数列{ab_n}是等差数列且公差为6.

答案：B