
题目列表(包括答案和解析)
21. (本小题满分12分)
一只口袋内装有形状、大小都相同的6只小球,其中4只白球,2只红球,从袋中随机摸出2只球。
(I)求2只球都是红球的概率;
(II)求至少有1只球是红球的概率。
20.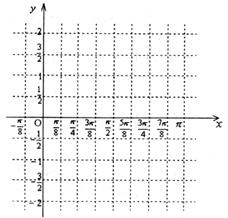 (本小题满分12分)
(本小题满分12分)
已知函数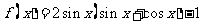
(I)求函数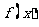 的最小正周期及单调递增区间;
的最小正周期及单调递增区间;
(II)画出函数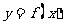 在区间
在区间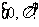 内的图像。
内的图像。
19. (本小题满分12分)
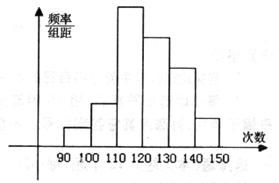 为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
为了了解高一学生的体能状况,某校抽取部分学生进行一分钟跳绳次数测试,将所得数据整理后,画出频率分布直方图(如图),图中从左到右各小长方形的面积之比为2:4:17:15:9:3,第二小组频数为12.
(I)求第二小组的频率;
(II)求样本容量;
(III)若次数在110以上为达标,试估计全体高一学生的达标率为多少?
17, (本小题满分10分)
已知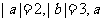 与
与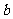 的夹角为120°。
的夹角为120°。
(I)求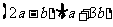 的值;
的值;
(II)当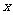 为何值时,
为何值时, 与
与 垂直。
垂直。
18.(本小题满份12分)
已知
(I)化简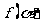
(II)若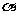 是第三象限角,且
是第三象限角,且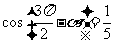 ,求
,求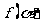 的值。
的值。
16. 给出下列四个命题:
①若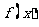 是定义在
是定义在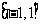 上的偶函数,且在
上的偶函数,且在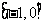 上
上
是增函数,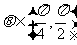 ,则
,则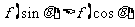 ;
;
②若锐角 满足
满足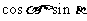 ,则
,则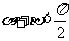 ;
;
③已知扇形的半径为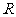 ,面积为
,面积为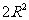 ,则这个扇形的圆
,则这个扇形的圆
心角的弧度数为4;
④要得到函数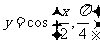 的图像,只需将
的图像,只需将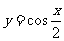 的图像向右平移
的图像向右平移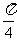 个单位。其中真命题的序号为
。
个单位。其中真命题的序号为
。
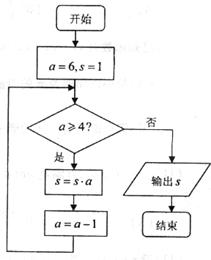
15.右图程序框的运行结果是 。
14. 某设备的使用年限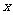 与所支出的总费用
与所支出的总费用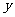 (万元)有如下的统计资料:
(万元)有如下的统计资料:
使用年限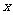 |
1 |
2 |
3 |
4 |
总费用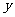 |
1.5 |
2 |
3 |
3.5 |
 由表中数据用最小二乘法得线性回归方程
由表中数据用最小二乘法得线性回归方程
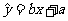 ,其中
,其中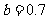 ,由此预测,当使用10年
,由此预测,当使用10年
时,所支出的总费用约为 万元。
13.如图,在平行四边形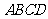 中,
中,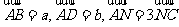 ,
,
则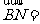 (用
(用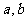 表示)
表示)
12. 设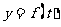 是某港口水的深度
是某港口水的深度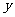 (米)关于时间
(米)关于时间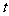 (时)的函数,其中
(时)的函数,其中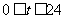 ,下表是该港口某一天从0时至24时记录的时间
,下表是该港口某一天从0时至24时记录的时间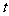 与水深
与水深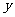 的关系:
的关系:
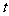 |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
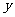 |
12 |
15.1 |
12.1 |
9.1 |
11.9 |
14.9 |
11.9 |
8.9 |
12.1 |
经长期观察,函数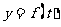 的图像可以近似地看成函数
的图像可以近似地看成函数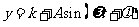 的图像,下面的函数中,最能近似表示表中数据间对应关系的函数是
的图像,下面的函数中,最能近似表示表中数据间对应关系的函数是
A、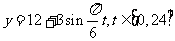 B、
B、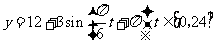
C、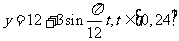 D、
D、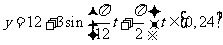
第II卷(非选择题,共90分)
11. 若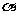 是锐角,且满足
是锐角,且满足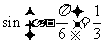 ,则
,则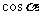 的值为
的值为
A、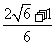 B、
B、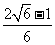 C、
C、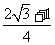 D、
D、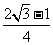
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com