
题目列表(包括答案和解析)
19.解:(Ⅰ)点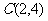 ………………………………1分
………………………………1分
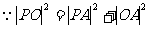 ,
,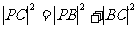 且
且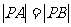 ,
,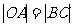
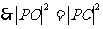 ,则
,则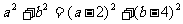 ………………………3分
………………………3分
即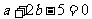 ………………………………4分
………………………………4分
(Ⅱ) 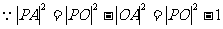
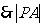 有最小值时,
有最小值时,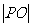 亦有最小值………………………………6分
亦有最小值………………………………6分
又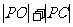 ≥
≥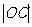 且
且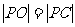
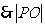 ≥
≥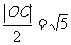
当且仅当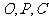 三点共线时取“=” ………………………………8分
三点共线时取“=” ………………………………8分
故
当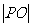 取最小值
取最小值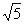 时,有
时,有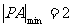 ………………………………10分
………………………………10分
(Ⅲ)不存在 ………………………………11分
若圆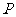 与圆
与圆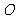 相内切,则圆
相内切,则圆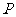 的半径
的半径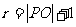 ……………………………12分
……………………………12分
若圆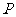 与圆
与圆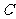 相外切,则圆
相外切,则圆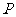 的半径
的半径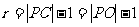 …………………13分
…………………13分
两者相互矛盾
即
不存在符合题设条件的圆 ………………………………14分
………………………………14分
18.解:(Ⅰ)如图

………………………………3分
(Ⅱ)所求多面体体积
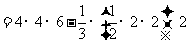
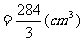 ……………………8分
……………………8分
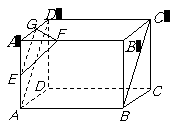
(Ⅲ)证明:在长方体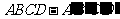 中,
中,
连结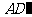 ,则
,则 .
.
因为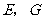 分别为
分别为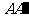 ,
, 中点,
中点,
所以 ,
,
从而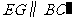 .又
.又 平面
平面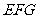 ,
,
所以 面
面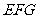 .························································································· 14分
.························································································· 14分
17.解: (Ⅰ) 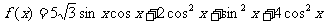
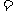
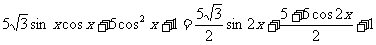
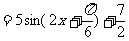 ………………………………4分
………………………………4分
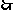 最小正周期
最小正周期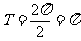 ,………………………………5分
,………………………………5分
由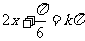 得
得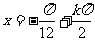 ,………………………………6分
,………………………………6分
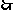
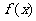 的对称中心为
的对称中心为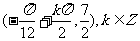 ………………………………7分
………………………………7分
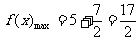 ,
,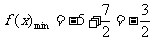 ………………………………9分
………………………………9分
(Ⅱ)由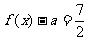 得
得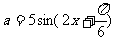 ………………………………10分
………………………………10分
当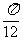 ≤
≤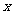 ≤
≤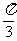 时,
时, 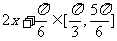
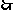
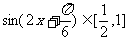 ……12分
……12分
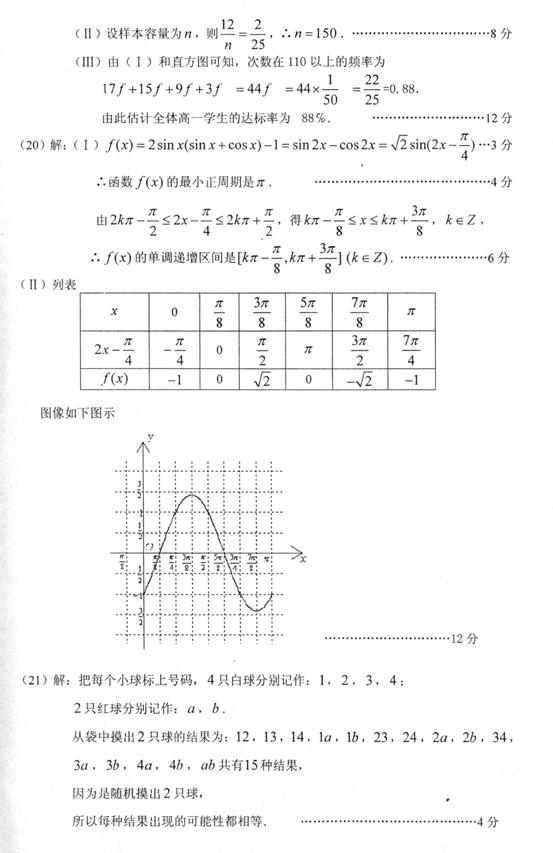
故函数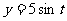 与
与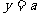 的图象在区间
的图象在区间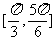 上有两个不同的交点
上有两个不同的交点
根据函数图象可得, 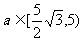 ………………………………14分
………………………………14分
16.解:(Ⅰ) 甲、乙两人下车的所有可能的结果为
(2,2),(2,3),(2,4),(3,2),(3,3),(3,4),(4,2),(4,3),(4,4) ………………………………6分
(Ⅱ)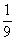 ………………………………9分
………………………………9分
(Ⅲ) 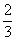 ………………………………12分
………………………………12分
15.解:(Ⅰ) 
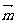 与
与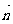 为共线向量,
为共线向量, 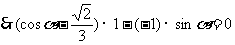 ,
,
即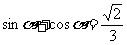 ………………………………4分
………………………………4分
(Ⅱ) 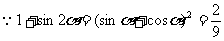 ,
,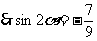 ……………………6分
……………………6分
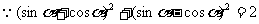 ,
,
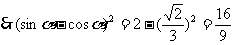 ………………………………8分
………………………………8分
又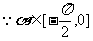 ,
,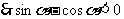 ,
, …………………10分
…………………10分
因此, 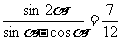 ………………………………12分
………………………………12分
11. 2 ;12. 小宇 ;13. 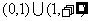 ;14.1000
;14.1000
 (15)(本小题满分12分)
(15)(本小题满分12分)
 已知向量
已知向量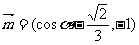 ,
,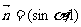 ,
,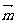 与
与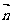 为共线向量,且
为共线向量,且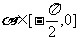
 (Ⅰ)求
(Ⅰ)求 的值;
的值;
 (Ⅱ)求
(Ⅱ)求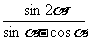 的值.。
的值.。



 (16)(本小题满分12分)
(16)(本小题满分12分)
 某市地铁全线共有四个车站,甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对
某市地铁全线共有四个车站,甲、乙两人同时在地铁第一号车站(首发站)乘车.假设每人自第2号车站开始,在每个车站下车是等可能的。约定用有序实数对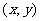 表示“甲在
表示“甲在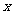 号车站下车,乙在
号车站下车,乙在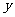 号车站下车”。
号车站下车”。
 (Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
(Ⅰ)用有序实数对把甲、乙两人下车的所有可能的结果列举出来;
 (Ⅱ)求甲、乙两人同在第3号车站下车的概率;
(Ⅱ)求甲、乙两人同在第3号车站下车的概率;
 (Ⅲ)求甲、乙两人在不同的车站下车的概率。
(Ⅲ)求甲、乙两人在不同的车站下车的概率。



 (17)(本小题满分14分)
(17)(本小题满分14分)
 已知
已知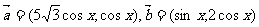 ,已知函数
,已知函数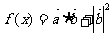
 (Ⅰ)求函数
(Ⅰ)求函数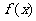 的最小正周期、对称中心及最值
的最小正周期、对称中心及最值
 (Ⅱ)当
(Ⅱ)当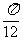 ≤
≤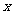 ≤
≤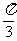 时,方程
时,方程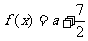 有两个不相等实根,求实数
有两个不相等实根,求实数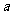 的取值范围.
的取值范围.



 (18)(本小题满分14分)
(18)(本小题满分14分)
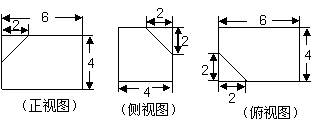
 如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在右面画出(单位:cm).
如下的三个图中,左面的是一个长方体截去一个角所得多面体的直观图,它的正视图和侧视图在右面画出(单位:cm).
 (Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
(Ⅰ)在正视图下面,按照画三视图的要求画出该多面体的俯视图;
 (Ⅱ)按照给出的尺寸,求该多面体的体积;
(Ⅱ)按照给出的尺寸,求该多面体的体积;
 (Ⅲ)在所给直观图中连结
(Ⅲ)在所给直观图中连结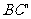 ,证明:
,证明: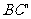 ∥面EFG。
∥面EFG。










 (19)(本小题满分14分)
(19)(本小题满分14分)
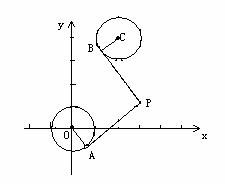
 已知圆
已知圆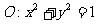 ,圆
,圆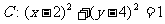 ,由两圆外一点
,由两圆外一点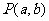 引两圆切线
引两圆切线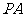 、
、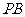 ,切点分别为
,切点分别为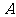 、
、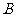 ,满足
,满足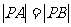
(Ⅰ)求实数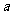 、
、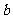 间满足的等量关系;
间满足的等量关系;
(Ⅱ)求切线长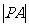 的最小值;
的最小值;
(Ⅲ)是否存在以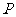 为圆心的圆,使它与圆
为圆心的圆,使它与圆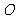 相内切并且与圆
相内切并且与圆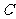 相外切?若存在,求出圆
相外切?若存在,求出圆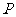 的方程;若不存在,说明理由。
的方程;若不存在,说明理由。
(20)(本小题满分14分)
已知函数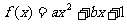 (
(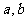 为实数),
为实数),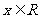 .
.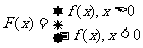
(Ⅰ)若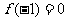 ,且函数
,且函数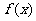 的值域为
的值域为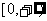 ,求
,求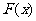 的表达式;
的表达式;
(Ⅱ)在(Ⅰ)的条件下,当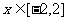 时,
时,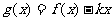 是单调函数,求实数
是单调函数,求实数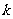 的取值范围;
的取值范围;
(Ⅲ)设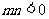 ,
,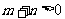 ,
, ,且
,且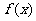 为偶函数,判断
为偶函数,判断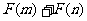 能否大于零。
能否大于零。
汕尾市08-09学年高一下学期期末考试
数学试题
 (11)下面的程序运行后第3个输出的数是 。
(11)下面的程序运行后第3个输出的数是 。
 i=1
i=1

 x=1
x=1
 DO
DO
 PRINT x
PRINT x
 i=i+1
i=i+1
 x=x+
x=x+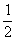
 LOOP UNTIL i=5
LOOP UNTIL i=5
 END
END
 (12)小桐和小宇的连续五次数学考试成绩用茎叶图表示如图,则从这五次考试成绩来看,成绩比较稳定的是 。
(12)小桐和小宇的连续五次数学考试成绩用茎叶图表示如图,则从这五次考试成绩来看,成绩比较稳定的是 。
 (13)函数
(13)函数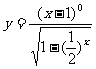 的定义域是 。
的定义域是 。
 (14)2008年5月12日,四川汶川发生里氏8.0级特大地震,给人民的生命财产造成巨大损失。里氏地震等级最早是在1935年由美国加州理工学院的地震学家里克特制定的,它同震源中心释放的能量(热能和动能)大小有关。震级
(14)2008年5月12日,四川汶川发生里氏8.0级特大地震,给人民的生命财产造成巨大损失。里氏地震等级最早是在1935年由美国加州理工学院的地震学家里克特制定的,它同震源中心释放的能量(热能和动能)大小有关。震级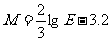 ,其中
,其中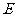 (焦耳)为地震时以地震波的形式释放出的能量。如果里氏6.0级地震释放的能量相当于一颗美国在二战投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于 颗广岛原子弹。
(焦耳)为地震时以地震波的形式释放出的能量。如果里氏6.0级地震释放的能量相当于一颗美国在二战投放在广岛的原子弹的能量,那么汶川大地震所释放的能量相当于 颗广岛原子弹。

(1)已知集合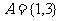 ,集合
,集合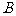 满足
满足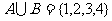 ,则集合
,则集合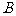 的个数是( )
的个数是( )
A.1 B.2 C.3 D.4
(2)若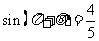 ,则
,则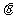 角的终边在( )
角的终边在( )
A.第一、二象限 B.第二、三象限 C.第一、四象限 D.第三、四象限
(3)若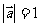 ,
,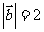 ,
,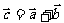 ,且
,且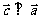 ,则向量
,则向量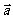 与
与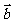 的夹角为( )
的夹角为( )
A.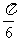 B.
B.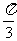 C.
C.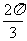 D.
D.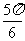
(4)某地一种植物一年生长的高度如下表:
高度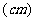 |
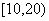 |
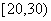 |
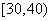 |
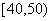 |
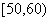 |
|
棵数 |
20 |
30 |
80 |
40 |
30 |
则该植物一年生长在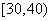 内的频率是( )
内的频率是( )
A.0.80 B.0.65 C.0.40 D.0.25
(5)有四个游戏盘,如下图所示,如果撒一粒黄豆落在阴影部分,则可中奖。小明希望中奖机会大,他应当选择的游戏盘为( )

A B C D
(6)若直线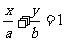 与圆
与圆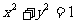 有公共点,则( )
有公共点,则( )
A. ≤
≤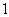 B.
B. ≥
≥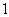
C.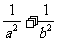 ≤
≤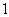 D.
D. ≥
≥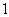
(7)设函数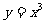 与
与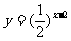 的图象的交点为
的图象的交点为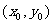 ,则
,则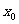 所在的区间是( )
所在的区间是( )
A.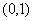 B.
B.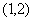 C.
C.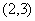 D.
D.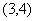
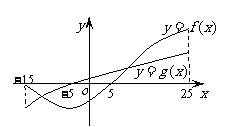 (8)已知函数
(8)已知函数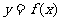 与
与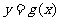 的图像如图所示,则不等式
的图像如图所示,则不等式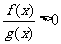 的解集是( )
的解集是( )
A.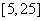 B.
B.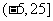
C.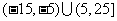 D.
D.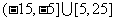
 (9)若定义在R上的函数
(9)若定义在R上的函数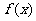 满足:对任意
满足:对任意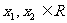 有
有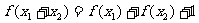 ,则下列说法一定正确的是( )
,则下列说法一定正确的是( )
A.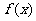 为奇函数 B.
为奇函数 B.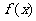 为偶函数
为偶函数
 C.
C.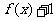 为奇函数 D.
为奇函数 D.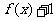 为偶函数
为偶函数
 (10)某商品进货规则是:不超过50件,按每件
(10)某商品进货规则是:不超过50件,按每件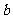 元,若超过50件,按每件
元,若超过50件,按每件 元。现进货不超过50件花了
元。现进货不超过50件花了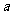 元,若在此基础上再多进11件,则花费仍为
元,若在此基础上再多进11件,则花费仍为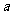 元,设进货价都是每件整元,则
元,设进货价都是每件整元,则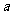 等于( )
等于( )
 A.1980 B.3690 C.6600 D.7200
A.1980 B.3690 C.6600 D.7200


 第二部分
非选择题(共100分)
第二部分
非选择题(共100分)

22. (本小题满分12分)
在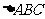 中,已知
中,已知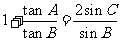 。
。
(I)求角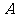 的大小;
的大小;
(II)若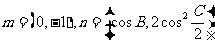 ,试求
,试求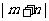 的最小值。
的最小值。


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com