
题目列表(包括答案和解析)
1.用定义
步骤:
例1.判断下列函数的奇偶性
(1)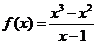 (2)
(2)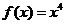 (3)
(3)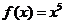 (4)
(4)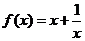
(5)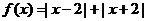 (6)
(6)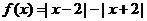
2.函数奇偶性的几个性质:
(1)奇偶函数的定义域关于原点对称;
(2)奇偶性是函数的整体性质,对定义域内任意一个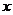 都必须成立;
都必须成立;
(3)奇函数的图像关于原点对称,偶函数的图像关于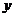 轴对称;
轴对称;
(4)根据奇偶性可将函数分为四类:奇函数、偶函数、既是奇函数又是偶函数、非奇非偶函数。
1.概念
对于函数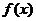 ,其定义域关于原点对称:
,其定义域关于原点对称:
如果______________________________________,那么函数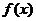 为奇函数;
为奇函数;
如果______________________________________,那么函数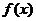 为偶函数.
为偶函数.
2.利用函数单调性定义证明函数f(x)=-x3+1在(-∞,+∞)上是减函数.
求函数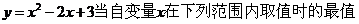 .
.
①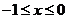 ②
②
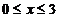 ③
③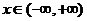
第六节 函数的奇偶性
1、下列函数中,在区间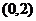 上递增的是
( )
上递增的是
( )
(A)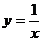 (B)
(B)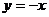 (C)
(C)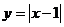 (D)
(D)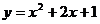
2. 如何求函数的最值;
(1)利用图象
例2. 已知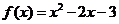 ,求下列各情况下的最值
,求下列各情况下的最值
(1)
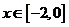 (2)
(2)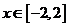 (3)
(3)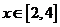
(2)利用单调性
例3.求函数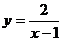 在区间[2,6]上的最大值和最小值。
在区间[2,6]上的最大值和最小值。
课后作业:
1. 最大值与最小值的定义
2. 如何用定义证明函数的单调性
步骤:
例1.
用定义证明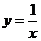 在
在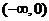 上是减函数
上是减函数
练习:(1)用定义证明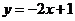 在R上是减函数
在R上是减函数
(2)用定义证明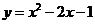 在
在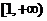 上是增函数
上是增函数
1. 通过观察图象,写出下列函数的单调区间
(1)一次函数;
(2)二次函数;
(3)反比例函数;
练习:在区间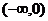 上为增函数的是 ( )
上为增函数的是 ( )
A.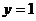 B.
B.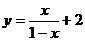 C.
C.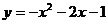 D.
D.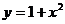
对于给定区间上的函数f(x)及属于这个区间上的任意两个自变量x1、x2,当x1<x2时,如果有f(x1)<f(x2),则称f(x)在这个区间上是____函数,这个区间就叫做函数f(x)的___区间;如果有f(x1)>f(x2),则称f(x)在这个区间上是____函数,这个区间就叫做函数f(x)的___区间; [说明] 1。单调区间是定义域的子集; 2。若函数f(x)在区间D上是增函数,则图象在D上的部分从左到右呈__趋势 若函数f(x)在区间D上是减函数,则图象在D上的部分从左到右呈__趋势 3。单调区间一般不能并
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com