
题目列表(包括答案和解析)
3. 已知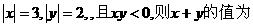 ____.
____.
2. 化简二次根式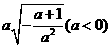 的结果是
的结果是
1. 等式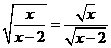 成立的条件是
( )
成立的条件是
( )
(A)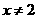 (B)
(B)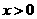 (C)
(C)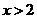 (D)
(D)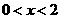
1.代数意义
练习:(1)① 若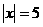 ,则x=____.
② 若
,则x=____.
② 若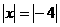 ,则x=____.
,则x=____.
③ 若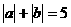 且a=-1,
则b=____;若
且a=-1,
则b=____;若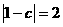 ,则c=____.
,则c=____.
④ 若 2a与1-a互为相反数,则a=____.
(2)下列说法中正确的是( )
A. 若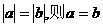 ;
B. 若
;
B. 若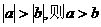
C. 若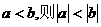 ; D. 若
; D. 若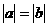 ,则
,则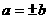 .
.
(3)已知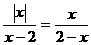 ,则x应满足________.
,则x应满足________.
(4)已知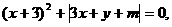 y为负数,则 m的取值范围是__________.
y为负数,则 m的取值范围是__________.
2.几何意义
例1. 说出下列各式的几何意义.
① 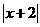 ②
②
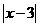 ③
③
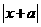
④ 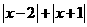 ⑤
⑤
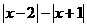
例2. 求满足下列各式的x的取值范围.
① 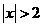 ②
② 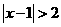 ③
③ 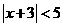
小结:不等式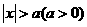 的解集是 ,不等式
的解集是 ,不等式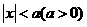 的解集是
的解集是
例3.(1)求满足下列各式的x的取值范围.
① 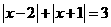 ②
②
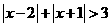 ③
③ 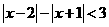
(2)① 若不等式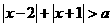 恒成立,求a的取值范围.
恒成立,求a的取值范围.
② 若不等式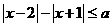 恒成立,求a的取值范围.
恒成立,求a的取值范围.
1.根式的概念
(1)根式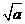 中a的取值范围是
;根式
中a的取值范围是
;根式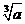 中a的取值范围是
中a的取值范围是
(2)性质: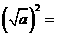 ,
, 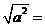 ;
;
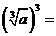 ,
, 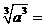
练习:(1)求使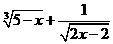 有意义的实数a的取值范围.
有意义的实数a的取值范围.
(2)当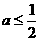 时,化简
时,化简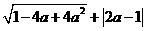 .
.
2.根式的运算
例1.(1)已知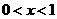 ,化简
,化简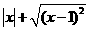 ;
;
(2)若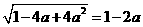 ,求a的取值范围.
,求a的取值范围.
例2. 化简下列各式
(1)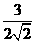 ; (2)
; (2)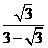 ; (3)
; (3)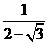 ; (4)
; (4)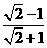 .
.
例3. 化简下列各式
(1)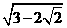 ;
(2)
;
(2)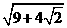 ;
(3)
;
(3)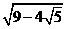
例4. 比较大小
(1)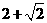 与
与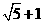 ;
(2)
;
(2)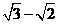 与
与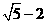 ;
;
练习:(1)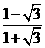 =__ ___;(2)比较大小:2- -(填“>”,或“<”).
=__ ___;(2)比较大小:2- -(填“>”,或“<”).
(3)若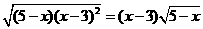 ,则
,则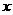 的取值范围是_ _ ___;
的取值范围是_ _ ___;
4. 你还记得在弧度制下弧长公式和扇形面积公式吗?(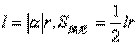 )
)
3. 你还记得三角化简的通性通法吗?(切割化弦、降幂公式、用三角公式转化出现特殊角. 异角化同角,异名化同名,高次化低次)
2. 在三角中,你知道1等于什么吗?(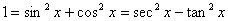
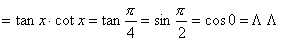 这些统称为1的代换) 常数 “1”的种种代换有着广泛的应用.
这些统称为1的代换) 常数 “1”的种种代换有着广泛的应用.
1. 在解三角问题时,你注意到正切函数、余切函数的定义域了吗?你注意到正弦函数、余弦函数的有界性了吗?
6. 正弦型函数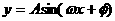 的对称轴为
的对称轴为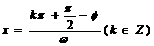 ;对称中心为
;对称中心为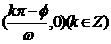 ;类似可得余弦函数型的对称轴和对称中心;
;类似可得余弦函数型的对称轴和对称中心;
〈三〉易错点提示:
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com