
题目列表(包括答案和解析)
4.若2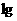 (x-2y)=
(x-2y)=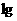 x+
x+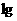 y,则
y,则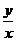 的值为( )
的值为( )
A.4 B.1或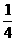 C.1或4 D.
C.1或4 D.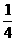
3.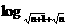 (
(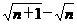 )等于( )
)等于( )
A.1 B.-1 C.2 D.-2
2.log7[log3(log2x)]=0,则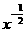 等于( )
等于( )
A.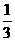 B.
B.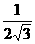 C.
C.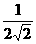 D.
D.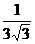
1.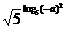 (a≠0)化简得结果是( )
(a≠0)化简得结果是( )
A.-a B.a2 C.|a| D.a
[考题1]求下列各式的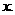
(1)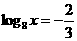 ;(2)
;(2)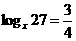 ;
;
(3)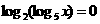 ;(4)
;(4)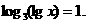
[解析](1)由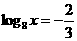 ,得
,得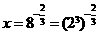 ,即
,即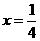 ;
;
(2)由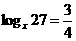 ,得
,得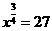 ,即
,即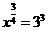 ,故
,故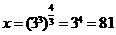 ;
;
(3)由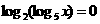 ,得
,得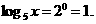 故
故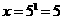 ;
;
(4)由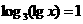 ,得
,得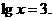 故
故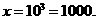
[点评]对数的定义是对数形式和指数形式互化的依据,而对数形式与指数形式的互化又是解决问题的重要手段。
[考题2]求下列各式的值:
(1)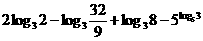 ;
;
(2)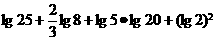 ;
;
(3)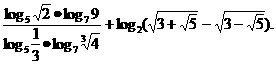
[分析]利用对数的性质求解,首先要明确解题目目标是化异为同,先使各项底数相同,才能使用性质,再找真数间的联系,对于复杂的真数,可以先化简再计算。
[解析](1)原式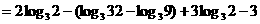
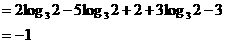
(2)原式=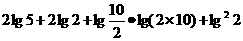
=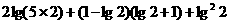 =
=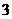
(3)∵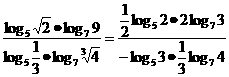
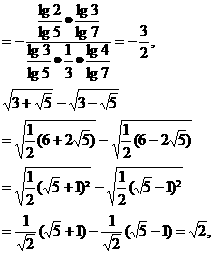
∴原式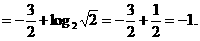
[点评]对数的求值一般有两种方法:一种是将式中真数的积、商、幂、方根利用对数的运算性质将它们化为对数的和、差、积、商,然后化简求值;另一种方法是将式中的和、差、积、商运用对数的运算法则将它们化为真数的积、商、幂、方根,然后化简求值。
[考题3]已知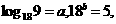 求
求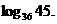
[解析]已知条件与所求对数的底是不相同的,因此考虑应用换底公式。
解法一:∵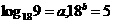 ,∴
,∴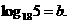
∴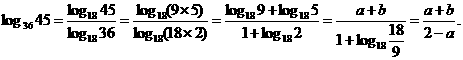
解法二:∵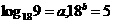 ,∴
,∴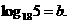
∴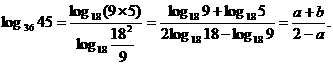
解法三:∵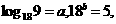
∴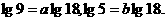
∴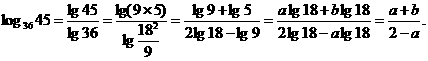
[点评]本题还有其他方法,这里,都是把指数式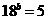 改写为对数式,再把所求对数通过换底公式换成和它相同底数的对数,以便利用已知条件和对数的性质求解。
改写为对数式,再把所求对数通过换底公式换成和它相同底数的对数,以便利用已知条件和对数的性质求解。
[考题4](1)设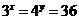 ,求
,求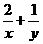 的值.
的值.
(2)已知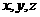 均大于1,
均大于1,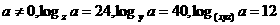 ,求
,求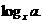
[分析](1)首先将指数式化为对数式,再利用对数的性质进行计算。(2)观察已知条件,真数相同,底数不同,若将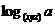 拆成
拆成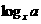 、
、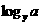 、
、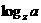 ,则问题获得解决,因此,要多次使用等式
,则问题获得解决,因此,要多次使用等式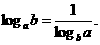
[解析](1)∵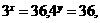
∴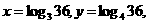
∴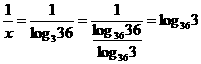 ,
,
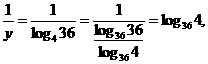
∴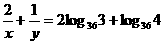
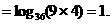
(2)由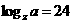 得
得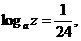
由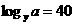 得
得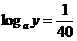 ,
,
由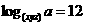 得
得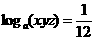 ,
,
即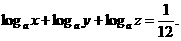
∴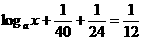 ,
,
解得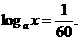
∴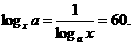
[点评](1)本题(1)通过将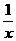 、
、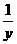 的值用换底公式转化为同底数的对数,再利用对数的运算法则求值,此外,我们还可以用换底公式得到一个常用的关系式
的值用换底公式转化为同底数的对数,再利用对数的运算法则求值,此外,我们还可以用换底公式得到一个常用的关系式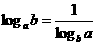 ,常用来把分式转化为整式。
,常用来把分式转化为整式。
(2)对数的换底公式在解题中起着重要的转化作用,能够将不同底的问题转化为同底,从而使我们利用对数的运算性质解题的想法得以实现。
[考题5]已知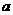 、
、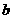 、
、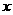 为正数,且
为正数,且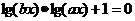 ,求
,求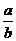 的取值范围.
的取值范围.
[解析]∵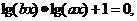
∴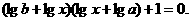
∴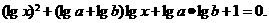
∵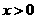 ,∴上式关于
,∴上式关于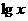 的方程有实根。
的方程有实根。
∴ .
.
∴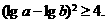
∴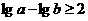 ,或
,或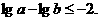
∴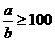 或
或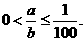
[点评]对数知识又常常与其他知识交汇在一起,构成较复杂的题目,如此题与方程、不等式综合,这时首先要牢牢掌握对数的定义,注意其与指数式的转化;灵活运用运算法则就可使问题得到解决。
[考题6]科学研究表明,宇宙射线在大气中能够产生放射性碳-14,碳-14的衰变极有规律,其精确性可以称为自然界的“标准时钟”。动植物在生长过程中衰变的碳-14,可以通过与大气的相互作用得到补充,所以活着的动植物每克组织中的碳-14含量保持不变,死亡后的动植物,停止了与外界环境的相互作用,机体中原有的碳-14按确定的规律衰减,我们已经知道其“半衰期”为5730年。
(1)设生物体死亡时,体内每克组织的碳-14含量为l,试推算生物死亡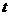 年后体内每克组织中的碳-14含量P;
年后体内每克组织中的碳-14含量P;
(2)湖南长沙马王堆汉墓女尸体出土时碳-14的残余量约占原始含量的76.7%,试推算马王堆古墓的年代。
[解析](1)设生物体死亡后时,体内每克组织中的碳-14的含量为1,1年后的残留量为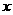 ,由于死亡机体中原有碳-14按确定的规律衰减,所以生物体的死亡年数
,由于死亡机体中原有碳-14按确定的规律衰减,所以生物体的死亡年数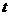 与其体内每克组织的碳-14含量P有如下关系:
与其体内每克组织的碳-14含量P有如下关系:
死亡年数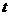 1 2 3 …
1 2 3 … 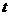 …
…
碳-14含量P 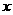
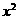
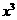 …
… 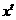 …
…
因此,生物死亡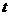 年后体内碳-14的含量
年后体内碳-14的含量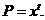
由于大约每过5730年,死亡生物体的碳-14含量衰减为原来的一半,所以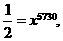
于是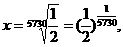
这样生物死亡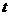 年后体内碳-14的含量
年后体内碳-14的含量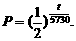
(2)由对数与指数的关系,指数式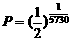 ,两边取常用对数得到
,两边取常用对数得到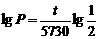 ,∴
,∴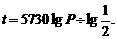
湖南长沙马王堆汉墓女尸中碳-14的残留量约占原始含量的76.7%,即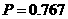 ,那么,那么
,那么,那么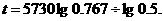
由计算器可算得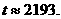
所以,马王堆古墓约是2100多年前的遗址。
[点评]要计算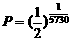 ,由于
,由于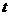 在指数上,计算是不可能的,当转为对数式可以计算其结果。
在指数上,计算是不可能的,当转为对数式可以计算其结果。
4.对数与指数式的关系及相互转换
利用对数式与指数式这一关系,可以把指数与对数进行互化,从而使问题顺利地得到解决,求某些对数值就可把它转化为指数问题。
3.换底公式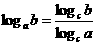
利用对数的换底公式,能够将一般对数式转化为自然对数或常用对数,为解决实际问题和数学计算带来方便。
(1)常用对数:对数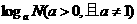 在底数
在底数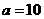 时,叫做常数对数,记作
时,叫做常数对数,记作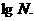
求一个正实数的常用对数,可通过对数表或使用计算器求解。
(2)自然对数:在科学技术中,常常使用以无理数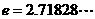 为底的对数,以e为底的对数叫做自然对数,
为底的对数,以e为底的对数叫做自然对数,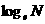 通常记作
通常记作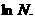
(3)自然对数与常用对数的关系:
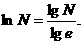
(4)要注意换底公式特点:
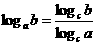
从左到右,将以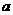 为底的对数换成了以
为底的对数换成了以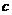 为底的对数,统一了底数,为计算带来了方便;从右至左,将分式化为整数,为化简带来了方便。
为底的对数,统一了底数,为计算带来了方便;从右至左,将分式化为整数,为化简带来了方便。
一般地,如果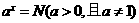 ,那么数
,那么数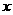 叫做以
叫做以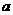 为底N的对数,记作
为底N的对数,记作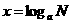 ,其中
,其中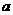 叫做对数的底数,N叫做真数。
叫做对数的底数,N叫做真数。
说明:(1)实质上,上述对数表达式,不过是指数函数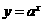 的另一种表达形式,例如:
的另一种表达形式,例如: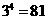 与
与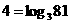 这两个式子表达是同一关系,因此,有关系式
这两个式子表达是同一关系,因此,有关系式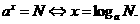
(2)“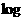 ”同“+”“×”“
”同“+”“×”“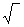 ”等符号一样,表示一种运算,即已知一个数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面。
”等符号一样,表示一种运算,即已知一个数和它的幂求指数的运算,这种运算叫对数运算,不过对数运算的符号写在数的前面。
(3)根据对数的定义,对数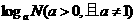 具有下列性质:
具有下列性质:
①零和负数没有对数,即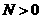 ;
;
②1的对数为零,即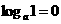 ;
;
③底的对数等于1,即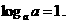
2.对数的运算法则
(1)基本公式:
①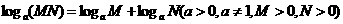 ,即正数的积的对数,等于同一底数的各个因数的对数的和。
,即正数的积的对数,等于同一底数的各个因数的对数的和。
②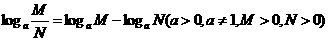 ,即两个正数的商的对数,等于被除数的对数减去除数的对数。
,即两个正数的商的对数,等于被除数的对数减去除数的对数。
③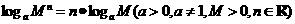 ,即正数的幂的对数等于幂的底数的对数乘以幂指数。
,即正数的幂的对数等于幂的底数的对数乘以幂指数。
(2)要熟练掌握公式的运用和逆用。
(3)在使用公式的过程中,要注意公式成立的条件。
例如:真数为两负数的积,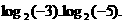 不能写成
不能写成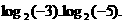 =
=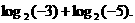
10、已知定义在实数集R上的偶函数,f(x)在[0,+∞)上为单调增函数, 若f(1) < f(lgx),求x的取值范围.
9、给它函数f(x) = 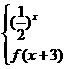
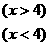 ,则f(log23)等于 ( )
,则f(log23)等于 ( )
A 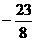 B
B 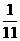 C
C 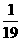 D
D 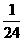
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com