
题目列表(包括答案和解析)
19.
解:在平面α内作AC⊥l于C,连结BC、PC.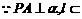 α,l⊥AC,∴l⊥PC即PC是P到l的距离.
α,l⊥AC,∴l⊥PC即PC是P到l的距离.
|
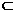 β,l⊥PC,∴l⊥BC. 即∠ACB为二面角α-l-β的平面角,∠ACB=θ,
β,l⊥PC,∴l⊥BC. 即∠ACB为二面角α-l-β的平面角,∠ACB=θ,
∵l⊥AC,l⊥PC,l⊥BC, ∴PACB是一个平面四边形. 又∠PAC=∠PBC=90°,∴四边形PACB内
接于以PC为直径的圆,∠APB=π-θ. 在△APB中,由余弦定理,得 AB2=PA2+PB2-2PA·PBcos
∠APB=m2+n2+2mncosθ. 由正弦定理,得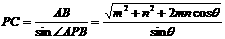 ,即为所求P到
,即为所求P到
l的距离.
18.
[解] (1)频率分布表如下:
|
身高 |
[122,126) |
[126,130) |
[130,134) |
[134。138] |
[138,142] |
[142,146 |
[146,150] |
[150,154] |
[154,158) |
|
人数 |
5 |
8 |
10 |
22 |
33 |
20 |
11 |
6 |
5 |
|
频率 |
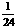 |
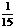 |
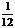 |
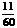 |
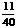 |
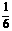 |
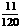 |
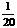 |
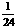
|
(2)频率分布直方图如图
(3)因为样本中身高在134-146cm的频率为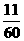 十
十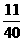 十
十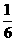 =0.625
=0.625
 所以本校同龄男孩身高在134-146cm的概率约为0.625。
所以本校同龄男孩身高在134-146cm的概率约为0.625。
[点拨] 这是第二种类型的总体分布,由于组距、分点巴定,故各组的频率可求。其中 134-146cm学生有3组,这三组的频率和就是身高在134-146cm的频率,用它可以估计相应概率.
17.
解 (1)设第i次抛掷硬币出现正面事件记为Ai,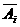 表示第i次抛掷硬币出现反面的事件(i=1,2,3,4,5),根据题意知Ai与
表示第i次抛掷硬币出现反面的事件(i=1,2,3,4,5),根据题意知Ai与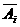 都是相互独立事件,且P(Ai)=P(
都是相互独立事件,且P(Ai)=P(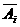 )=
)=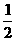 .
.
第一次、第四次出现正面,另外三次出现反面的事件为A1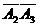 A4
A4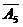 。
。
则P(A1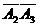 A4
A4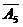 )=P(A1)P(
)=P(A1)P(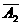 )P(
)P( )P(A4)P(
)P(A4)P(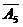 )=P((A1)×P(
)=P((A1)×P(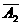 )×P(
)×P( )×P(A4)×P(
)×P(A4)×P(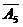 )=
)=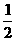 ×
×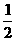 ×
×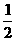 ×
×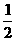 ×
×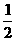 =
= 。
。
答:第一次、第四次出现正面,另三次出现反面概率为 .
.
(2)由于每次抛掷出现正面的概率是相同的,所以两次出现正面,三次出现反面的事件就是五次独立重复试验中,正面恰好出现两次.根据n次独立重复试验中某个事件发生n次的概率公式,得所求的概率为P5(2)=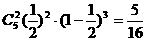
答;两次出现正面,三次出现反面概率为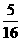 .
.
22.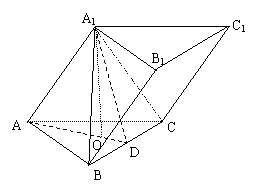 斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面的射影O是△ABC的中心,异面直线AB与CC1所成的角为45°.
斜三棱柱ABC-A1B1C1的底面是边长为2的正三角形,顶点A1在底面的射影O是△ABC的中心,异面直线AB与CC1所成的角为45°.
(1) 求证:AA1⊥平面A1BC;
(2) 求二面角A1-BC-A的平面角的正弦值;
(3) 求这个斜三棱柱的体积.
高二数学综合训练(三)答案
21.矩形ABCD的两个顶点A、B在x轴上,另两个顶点C、D在抛物线y=4-x2位于x轴上方的曲线上,求矩形ABCD的面积最大值。
20、若某一等差数列的首项为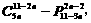 ,公差为
,公差为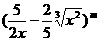 的常数项,其中m是
的常数项,其中m是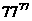 -15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
-15除以19的余数,则此数列前多少项的和最大?并求出这个最大值。
19.已知二面角α-l-β等于θ,PA⊥α,PB⊥β,A、B为垂足,若PA=m,PB=n,求P到棱l的距离.
18.下表给出了某校120名12岁男孩身高的资料.
|
身高 |
[122,126) |
[126,130) |
[130,134) |
[134,138) |
[138,142) |
|
人数 |
5 |
8 |
10 |
22 |
33 |
|
身高 |
[142,146] |
[146,150) |
[150,154) |
[154,158) |
|
|
人数 |
20 |
11 |
16 |
5 |
|
(1)列出样本的频率分布表并画出直方图.
(2)根据上述抽样结果,估计本校同龄男孩身高在134-146cm的概率有多大?
17.将一枚均匀硬币抛掷5次,
(1)求第一次、第四次出现正面,而另外三次都出现反面的概率;
(2)求两次出现正面。三次出现反面的概率.
16. P、Q是半径为R的球面上的两点,它们的球面距离是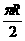 ,则过P、Q的平面中,与球心的最大距离是
,则过P、Q的平面中,与球心的最大距离是
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com