
题目列表(包括答案和解析)
24.从5双不同号码的鞋子中任取4只,求这4只鞋子中至少有2只可配成一双的概率。
解:记事件 =“4只鞋中至少有两只配成一双”,
=“4只鞋中至少有两只配成一双”,  =“4只中恰好有2只配成一双”,
=“4只中恰好有2只配成一双”,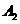 =“4只中恰好配成两双”,
=“4只中恰好配成两双”,  与
与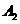 互斥,
互斥,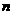 =
=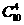 ,事件
,事件 包含的基本事件数
包含的基本事件数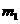
先从5双鞋中任选取一双,有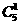 种选法,把选中的一双2只都取出来有
种选法,把选中的一双2只都取出来有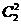 种选法,再在剩下的4双中任取2双有
种选法,再在剩下的4双中任取2双有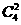 种选法,每双任取一只有
种选法,每双任取一只有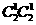 种,所以有
种,所以有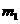 =
=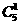
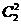
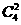
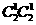
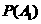 =
=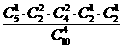
事件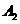 包含的基本事件数
包含的基本事件数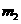
先从5双中任取2双,有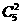 种选法,把选中的2双4只都取出来有
种选法,把选中的2双4只都取出来有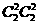 种选法,所以
种选法,所以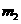 =
=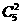
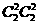
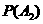 =
=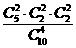
∴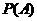 =
=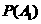 +
+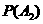 =
=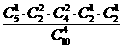 +
+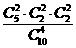 =
=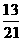
23.求所有三位数中,含有两个相同数字的三位数的概率。
分析: 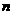 =
=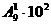 =900,
=900, =243,这一步可分类计算:
=243,这一步可分类计算:
0在内,则三位数形如: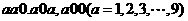 有27个;
有27个;
0 不在内,则三位数形如: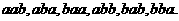
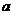 、
、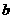 是从1到9中任取2个,所以共有
是从1到9中任取2个,所以共有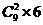 =216个,所以
=216个,所以 =27+216=243。
P(A)=
=27+216=243。
P(A)=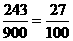
22.某产品中有15只正品,5只次品,每次取1只测试,取后不放回,直到5只次品全部测出为止,求经过10次测试,5只次品全部发现的概率。 (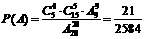 )
)
21.一架电梯开始时有6位乘客并停于十层楼的每一层,求下列事件的概率:
(1)“某指定的一层有两位乘客离开”
(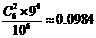 )
)
(2)“没有两位及两位以后的乘客在同一层离开” (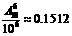 )
)
(3)“恰有两位乘客的同一层离开”
(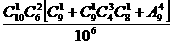 )
)
(4)“至少有两位乘客在同一层离开” (1-0.1512=0.8488)
20.某参观团共有8人,将进入10个房间,如果每个房间进入人数不限,每人进入每个房间都是等可能的,求下列事件上的概率:
(1) =“某指定8房中各有1人”;
(
=“某指定8房中各有1人”;
(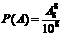 )
)
(2)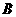 =“恰有8间房,其中各有1人” (
=“恰有8间房,其中各有1人” ( )
)
(3)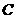 =“某指定房间中恰有3人”
(
=“某指定房间中恰有3人”
(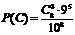 )
)
变1:如将第上题中的“房间”换成“车站”可改为如下形式:有8个乘客乘公共汽车,途经10个车站,假定每个乘客都可能在每个车站下车,试求下列事件的概率:
(1) =“在指定8个车站,每站下车1人”;
=“在指定8个车站,每站下车1人”;
(2)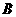 =“恰有8个车站,每站下车 1人”
=“恰有8个车站,每站下车 1人”
(3)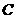 =“某指定的车站恰有3人”
=“某指定的车站恰有3人”
变2:将上例中的“10”换成正整数“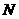 ”,将“8”换成正整数“
”,将“8”换成正整数“ ”(
”(  ≤
≤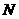 )则具有以下形式:
)则具有以下形式:
将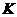 个不同的球随机地放入
个不同的球随机地放入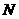 个盒子中去(
个盒子中去(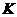 ≤
≤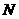 )。假设每个盒子能容纳的球数不限,求下列事件的概率。
)。假设每个盒子能容纳的球数不限,求下列事件的概率。
(1) 指定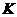 个盒子各一个球;(2)恰有
个盒子各一个球;(2)恰有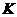 个盒子各一个球。
个盒子各一个球。
解:把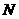 个盒子看作“房间”,球视为“人”,问题变为将“人”分配进“房间”,本题形似“摸球”而实际上属“分房问题”。
个盒子看作“房间”,球视为“人”,问题变为将“人”分配进“房间”,本题形似“摸球”而实际上属“分房问题”。
变3:将例中的“房间”换成“天”,“10”换成“365”,“8”换成“ ”则有如下的生日问题:
”则有如下的生日问题:
设有 个人,
个人, ≤365,并设每人的生日在一年的365天中的每一天是均等的,问此
≤365,并设每人的生日在一年的365天中的每一天是均等的,问此 个人有不同生日的概率是多少?
个人有不同生日的概率是多少?
解:所求概率的事件相当于例9中的事件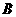 ,这里我们不妨仍设为
,这里我们不妨仍设为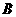 ,类似地例中的求法,
,类似地例中的求法,
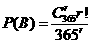 =
=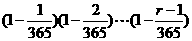
当 较小时,
较小时,
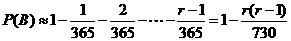
如取 =2,得两人不同生日的概率为
=2,得两人不同生日的概率为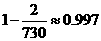
19.一批产品共100件,其中一等品有40件,二等品有60件,今从这批产品中任
意抽取3件,在下列抽取方式中,求抽出的三件中有两件是一等品,一件是二等品的概率。
有返回抽样:每次取一件,检查后放回,然后再抽取下一件。(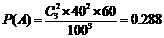 )
)
不返回抽样:每次抽取一件,检查后不放回,在剩下的产品中再抽取下一件。(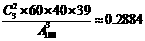 )
)
17. 甲、乙两名运动员进行乒乓球单打比赛。根据以往的比赛情况,每一局甲胜的概率为0.6,乙胜的概率为0.4。如果比赛时采用三局二胜制或五局三胜制,问哪一种赛制下甲胜的可能性较大?
解:(1)三局二胜制甲胜的概率=0.648。
(2)五赛三胜制甲胜的概率为=0.682。甲在“五局三胜”中获胜的可能性较大。
在第1,3,5,8路公共汽车都要停靠的一个站(假定这个站只能停靠一辆汽车),有18。一位乘客等候第1路或第3路汽车,假定当时各路汽车首先到站的可能性相等,求首先到站正好是这位乘客所要乘的汽车的概率。
解:由题意知共有4路车可在此站停靠,而且每路车首先到站的可能性相等,故基本事件共有4个,且每一个的发生都是等可能的,即基本事件总数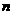 =4。
=4。
设 表示首先到站正好是1路或3路汽车这一事件,则
表示首先到站正好是1路或3路汽车这一事件,则 所包含的基金事件数
所包含的基金事件数 =2。故所求概率=
=2。故所求概率=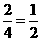
16.金工车间有10台同类型的机床,每台配备的电动机的功率为10千瓦。已知每台机床工作时,平均每小时实际开动12分钟,且开动与否是相互独立的。如因特殊情况,供电部门只提供50千瓦的电力给这10台机床,问这10台机床能够正常工作的概率为多大?
解:50千瓦可供给5台机床开动,因而10台机床中同时开动的台数不超过5台时都可以正常工作。又每台机床只有“开动”与“不开动”两种情况,且“开动”的概率为12/60=1/5,“不开动”的概率为4/5。
设10台机床中正在开动着的机床的台数为k,则
P (k)=
(k)=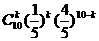 ,0≤k≤10
,0≤k≤10
于是同时开动着的机床的台数不超过5台的概率为
P(k≤5)= ≈0.994。
由此可知这10台机床的工作基本上不受电力供应紧张的影响,因为在电力供应为50千瓦的条件下,机床不能正常工作(同时开动6台或6台以上)的概率0.006,是一个小概率事件。
13. 在人寿保险事业中,很重视某一年龄的投保人的死亡率,假如1个投保人能活到65岁的概率为0.6,试问;
(1)3个投保人全部活到65岁的概率;
(P3(3)=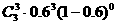 =0.216;)
=0.216;)
(2)3个投保人有2个活到65岁的概率;
(P3(2)=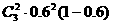 =0.432;)
=0.432;)
(3)3个投保人有1个活到65岁的概率;
(P3(1)=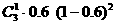 =0.288;)
=0.288;)
(4)3个投保人都活不到65岁的概率.
(P3(0)=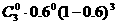 =0.064。)
=0.064。)
14 对某种药物的疗效进行研究,假定药物对某种疾病的治愈率为0.8,现在10个患此病的病人同时服用此药,求其中至少有6个病人治愈的概率.
解:设病人服用该药后治愈记为事件A,没有治愈记为事件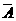 ,则根据题意,有P(A)=0.8,P(
,则根据题意,有P(A)=0.8,P(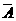 )=1一P(A)=0。2. 至少有6个治愈可分为10人中6人治愈、7人治愈,8人治愈,9人治愈,10人治愈.
)=1一P(A)=0。2. 至少有6个治愈可分为10人中6人治愈、7人治愈,8人治愈,9人治愈,10人治愈.
所以,所求概率为P=P10(6)+P10 (7)十P10 (8)十P10 (9)十P10 (10) =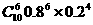 +
+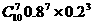 +
+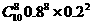 +
+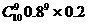 +
+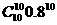 =0.97
=0.97
15 某种大炮击中目标的概率是0.3,只要以多少门这样的大炮同时射击1次,就可以使击中目标的概率超过95%?
解 因为大炮击中目标的概率为0.3,所以大炮不击中目标的概率为0.7,n门大炮都击不中目标的概率是0.7n.因此,其中至少1门大炮击中目标的概率是1一0.7n,根据题意,有1一0.7n>0.95,
即0.7n<0.05, 两边取对数后,解不等式得 n>
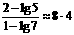 .
.
即要以9门大炮同时射击1次,就可使击中目标的概率超过95%。
11.某商场为迎接国庆举办新产品问世促销 活动,方式是买-份糖果摸一次彩,模彩的器具是绿、白两色的乒乓球.这些乒乓球的大小和质料完全相同.商场拟按中奖率1%设大 奖,其余99%为小奖.为了制定摸彩的办法, 商场向职工广泛征集方案,对征集到的优秀 方案进行奖励.如果你是此商场职工,你将会提出怎样的方案?
注:商场提供的模彩器材是棱长约30cm 的立方体形木箱,密封良好,不透光、木箱上 方可容一只手伸入,另备足够多的白色乒乓球和少量绿色乒乓球。
方案一: 在箱内放置100个乒乓球,其中1个为绿色乒乓球,其余99个为白色乒乓球,顾客一次模出1个乒乓球,如果为绿色乒乓球,即中大奖,否则中小奖,本方案中大奖的概率为: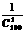 =
=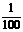 。
。
方案二: 在箱内放置14个乒乓球,其中2个为绿色乒乓球,其余12个为白色乒乓球。顾客--次摸出2个乒乓球为绿色,即中大奖;如果模出的2个乒乓球为白色,或1个为白色、1个为绿色。则中小奖.本方案中大奖的概率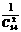 =
=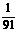 。
。
方案三:在箱内放置15个乒乓球,其中2个为绵色乒乓球,其余13个为白色乒乓球.顾客摸球和中奖的办法与方案二相同.本方案中大奖的概率为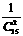 =
=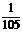
方案四: 在箱内放置25个乒乓球,其中3个为绿色乒乓球,其余22个为白色乒乓球.顾客一次摸出2个乒乓球(或分两次模,每次摸一个乒乓球,不放回),如果摸出的2个乒乓球为绿色,即中大奖;如果模出的2个乒乓球为白色或1个为白色、1个为绿色,则中小奖.本方案中大奖的概率为 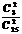 =
=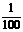 。
。
12 设甲、乙两射手独立地射击同一目标,他们击中目标的概率分别为0.95,0.9.
求:(1)在一次射击中,目标被击中的概率; (2)目标恰好被甲击中的概率.
解 设甲击中目标事件为A,乙击中目标为事件B,根据题意,有P(A)=0.95,P(B)=0.9
(1) P(A·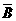 +
+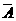 ·B+A·B)=P(A·
·B+A·B)=P(A·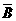 )十P(
)十P(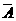 ·B)十P(A·B) =P(A)·P(
·B)十P(A·B) =P(A)·P(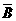 )十P(
)十P(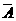 )·P(B)十P(A)·P(B)
)·P(B)十P(A)·P(B)
=0.95×(1-0.9)十(1-0.95)×O.9十0.95×0.90 =0.995。
(2) P(A·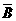 )=P(A) ·P(
)=P(A) ·P(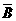 )=0.95×(1一0。90)=0.095.
)=0.95×(1一0。90)=0.095.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com