
题目列表(包括答案和解析)
7.甲、乙两位同学上课后独立完成5道自我检测题,甲及格概率为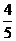 ,乙及格概率为
,乙及格概率为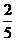 ,
,
则两人中至少有一人及格的概率为( )
A.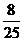 B.
B.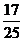 C.
C.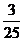 D.
D.
6.若双曲线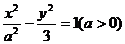 的离心率为2,则双曲线的渐近线方程为( )
的离心率为2,则双曲线的渐近线方程为( )
A.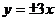 B.
B.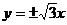 C.
C.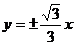 D.
D.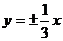
5.已知随机变量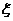 服从正态分布
服从正态分布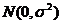 ,且
,且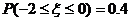 ,则
,则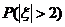 的值为( )
的值为( )
A.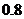 B.
B.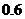 C.
C.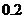 D.
D.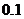
4. 已知抛物线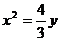 ,则它的焦点坐标是( )
,则它的焦点坐标是( )
A.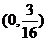 B.
B.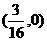 C.
C.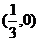 D.
D.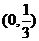
3.命题“对任意的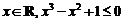 ”的否定是( )
”的否定是( )
A.不存在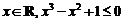 B.存在
B.存在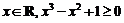
C.对任意的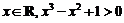 D.存在
D.存在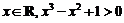
2.已知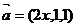 ,
,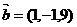 ,如果
,如果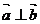 ,则
,则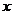 的值为( )
的值为( )
A.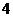 B.
B.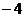 C.
C.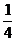 D.
D.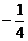
中,只有一项是符合题目要求的。(把答案填在答题卡上)
1.“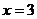 ”是“
”是“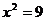 ”的( )
”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
46. (本题满分18分)第一题满分5分,第二题满分5分,第三题满分8分.
如图,有一公共边但不共面的两个三角形ABC和A1BC被一平面DEE1D1所截,若平面DEE1D1分别交AB,AC,A1B,A1C于点D,E,D1,E1。
(1)讨论这三条交线ED,CB, E1 D1的关系。
(2)当BC//平面DEE1D1时,求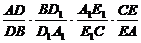 的值。
的值。

(3)当BC不平行平面DEE1D1时, 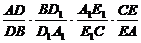 的值变化吗?为什么?
的值变化吗?为什么?

(1)互相平行或三线共点。
当BC//平面DEE1D1时,
平面ABC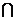 平面DEE1D1=ED
平面DEE1D1=ED
BC// ED,同理CB// E1 D1
∴ED//CB// E1 D1
当BC不平行平面DEE1D1时,
延长ED、CB交于点H,
∴H∈EF ∵EF 平面DEE1D1 ∴H∈平面DEE1D1
平面DEE1D1 ∴H∈平面DEE1D1
同理H∈平面A1BC
∴H∈平面DEE1D1∩平面A1BC
即H∈E1D1 ∴E1、D1、H三点共线
∴三线共点
(2)解:∵BC//平面DEE1D1
且BC 平面ABC,平面ABC∩平面DEE1D1=ED
平面ABC,平面ABC∩平面DEE1D1=ED
∴BC∥ED,同理BC∥E1D1
在△ABC中,BC∥ED
∴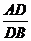 =
=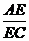 同理可得
同理可得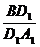 =
=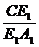
∴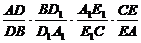 =
=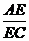
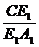
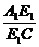
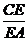 =1
=1
(3)解:
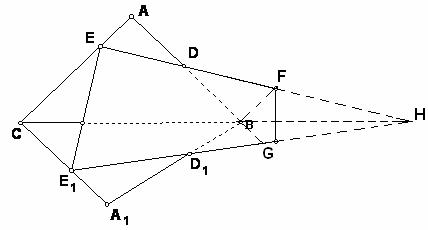
由(1)可得,延长ED、CB、E1D1交于点H,
过点B作BF∥AC,BG∥A1C
∵BF∥AC ∴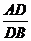 =
=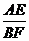
同理可得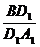 =
=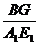
在△HCE中,BG∥CE1 ∴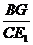 =
=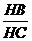
同理可得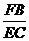 =
=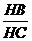
∴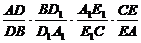 =
=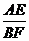
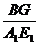
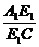
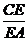 =
=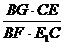 =
=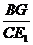
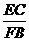 =
=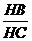
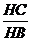 =1
=1
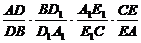 的值不变化,仍为1
的值不变化,仍为1
45. (本题满分16分)第一题满分4分,第二题满分6分,第三题满分6分.
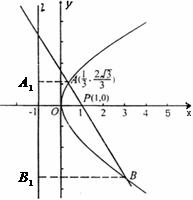
已知动圆过定点P(1,0),且与定直线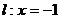 相切。
相切。
(1)求动圆圆心的轨迹M的方程;
(2)设过点P,且倾斜角为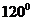 的直线与曲线M相交于A,B两点,A,B在直线
的直线与曲线M相交于A,B两点,A,B在直线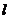 上的射影是
上的射影是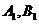 。求梯形
。求梯形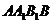 的面积;
的面积;
(3)若点C是(2)中线段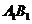 上的动点,当△ABC为直角三角形时,求点C的坐标。
上的动点,当△ABC为直角三角形时,求点C的坐标。
解: (1)曲线M是以点P为焦点,直线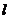 为准线的抛物线,其方程为
为准线的抛物线,其方程为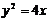 .
.
(2)由题意得,直线AB的方程为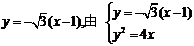 消y得
消y得
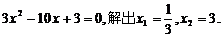
于是, A点和B点的坐标分别为A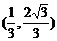 ,B(3,
,B(3,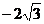 ),
),
所以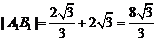 ,
,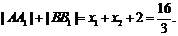
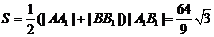
(3)设C(-1,y)使△ABC成直角三角形,
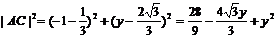 ,
,
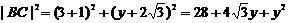 ,
,
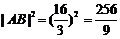 .
.
(i) 当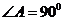 时,
时,
方法一:当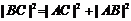 时,
时,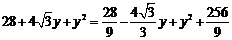 ,
,
即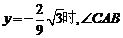 为直角. C点的坐标是
为直角. C点的坐标是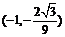
方法二:当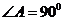 时,得直线AC的方程为
时,得直线AC的方程为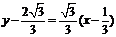 ,
,
求得C点的坐标是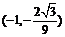 。
。
(ii) 因为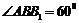 ,所以,
,所以,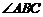 不可能为直角.
不可能为直角.
(iii) 当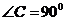 时,
时,
方法一:当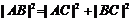 时,
时,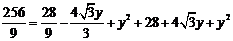 ,
,
即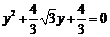 ,解得
,解得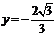 ,此时
,此时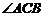 为直角。
为直角。
方法二:当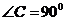 时,由几何性质得C点是
时,由几何性质得C点是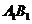 的中点,即C点的坐标是
的中点,即C点的坐标是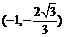 。
。
故当△ABC为直角三角形时,点C的坐标是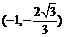 或
或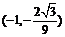
44. (本题满分14分)第一题满分4分,第二题满分4分,第三题满分6分.
甲乙二人用4张扑克牌(分别是红桃2,红桃3,红桃4,方片4)玩游戏,他们将4张扑克牌洗匀后,背面朝上放在桌面上,甲先抽,乙后抽,抽出的牌不放回,各抽一张。
(1)设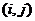 分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示),写出甲乙二人抽到的牌的所有情况;
分别表示甲、乙抽到的牌的数字(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示),写出甲乙二人抽到的牌的所有情况;
(2)若甲抽到红桃3,则乙抽出的牌的牌面数字比3大的概率是多少?
(3)甲乙约定:若甲抽到的牌的牌面数字比乙大,则甲胜;若甲抽到的牌的牌面数字不比乙大,则乙胜。你认为此游戏是否公平,说明你的理由。
解:(1)甲乙二人抽到的牌的所有情况(方片4用4’表示,红桃2,红桃3,红桃4分别用2,3,4表示)为:
(2,3)、(2,4)、(2,4’)、(3,2)、(3,4)、(3,4’)、
(4,2)、(4,3)、(4,4’)、(4’, 2)、(4’,3)(4’,4)
共12种不同情况
(没有写全面时:只写出1个不给分,2-4个给1分,5-8个给2分,9-11个给3分)
(2)甲抽到3,乙抽到的牌只能是2,4,4’
因此乙抽到的牌的数字大于3的概率为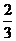
(3)由甲抽到的牌比乙大的有
(3,2)、(4,2)、(4,3)、(4’,2)、(4’,3)5种,
甲胜的概率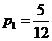 ,乙获胜的概率为
,乙获胜的概率为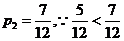
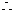 此游戏不公平。
此游戏不公平。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com