
题目列表(包括答案和解析)
19.已知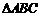 的内角A、B、C的对边分别为a、b、c,
的内角A、B、C的对边分别为a、b、c,
且满足
(1)证明: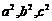 成等差数列且
成等差数列且 B≤
B≤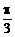 ;
;
(2)求函数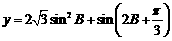 的最大值.
的最大值.
解:(1) 

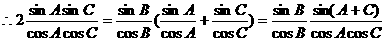
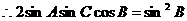
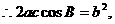
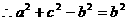
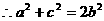

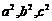 成等差数列
成等差数列
由余弦定理,得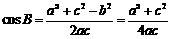 .
.
因为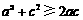 ,
,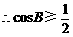 .
.
由0<B<π,得 B≤
B≤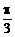
(2)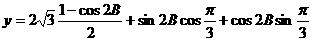
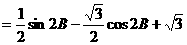
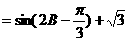

 B≤
B≤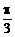
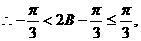
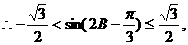
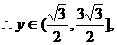
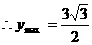
18. 已知分别以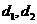 为公差的等差数列
为公差的等差数列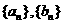 满足
满足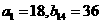 。
。
(1)若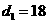 ,且存在正整数
,且存在正整数 ,使得
,使得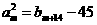 ,求证:
,求证: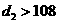 ;
;
(2)若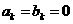 ,且数列
,且数列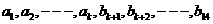 的前
的前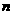 项和
项和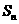 满足
满足
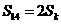 ,求数列
,求数列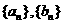 的通项公式;
的通项公式;
(3)
在(2)的条件下,令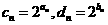 ,问不等式
,问不等式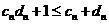 是否对
是否对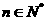 恒成立?请说明理由。
恒成立?请说明理由。
解:(1)依题意,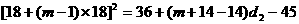 ,
,
即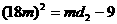 , 即
, 即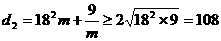 ;
;
等号成立的条件为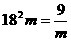 ,即
,即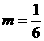 ,
,
 ,
, 等号不成立,
等号不成立, 原命题成立.
原命题成立.
(2)由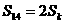 得:
得: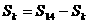 ,即:
,即: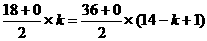 ,
,
则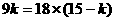 ,得
,得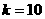
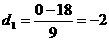 ,
,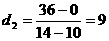 ,则
,则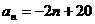 ,
,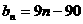 ;
;
(3)在(2)的条件下,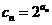 ,
,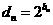 ,
,
要使 ≤
≤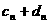 ,即要满足
,即要满足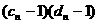 ≤0,
≤0,
又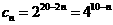 ,
,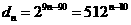 ,∴数列
,∴数列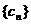 单调减;
单调减;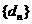 单调增,
单调增,
①
当正整数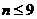 时,
时,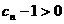 ,
,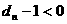 ,
,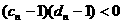 ;
;
②
当正整数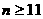 时,
时,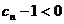 ,
,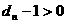 ,
,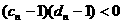 ;
;
③ 当正整数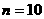 时,
时,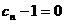 ,
,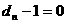 ,
,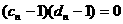 ,
,
综上所述,对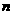 ∈N+,不等式
∈N+,不等式 ≤
≤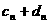 恒成立.
恒成立.
17. 过点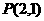 的直线
的直线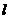 交
交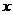 轴、
轴、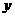 轴正半轴于
轴正半轴于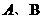 两点,求使:
两点,求使:
(1)△ 面积最小时
面积最小时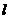 的方程;
的方程;
(2)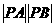 最小时
最小时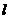 的方程.
的方程.
解 方法一 设直线的方程为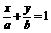 (a>2,b>1),
(a>2,b>1),
由已知可得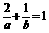 . (1)∵2
. (1)∵2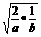 ≤
≤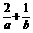 =1,∴ab≥8.∴S△AOB=
=1,∴ab≥8.∴S△AOB=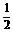 ab≥4.
ab≥4.
当且仅当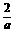 =
=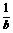 =
=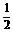 ,即a=4,b=2时,S△AOB取最小值4,
,即a=4,b=2时,S△AOB取最小值4,
此时直线l的方程为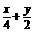 =1,即x+2y-4=0.
=1,即x+2y-4=0.
(2)由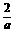 +
+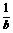 =1,得ab-a-2b=0,变形得(a-2)(b-1)=2,
=1,得ab-a-2b=0,变形得(a-2)(b-1)=2,
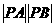 =
=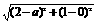 ·
·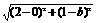
=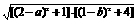 ≥
≥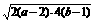 . 当且仅当a-2=1,b-1=2,即a=3,b=3时,|PA|·|PB|取最小值4.
. 当且仅当a-2=1,b-1=2,即a=3,b=3时,|PA|·|PB|取最小值4.
此时直线l的方程为x+y-3=0.
方法二 设直线l的方程为y-1=k(x-2) (k<0),
则l与x轴、y轴正半轴分别交于A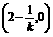 、B(0,1-2k).
、B(0,1-2k).
(1)S△AOB=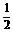
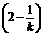 (1-2k)=
(1-2k)=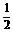 ×
×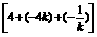 ≥
≥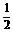 (4+4)=4.
(4+4)=4.
当且仅当-4k=-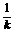 ,即k=-
,即k=-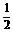 时取最小值,此时直线l的方程为y-1=-
时取最小值,此时直线l的方程为y-1=-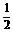 (x-2),即x+2y-4=0.
(x-2),即x+2y-4=0.
|
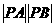 =
=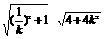 =
=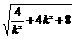 ≥4,
≥4,
当且仅当 =4k2,即k=-1时取得最小值,此时直线l的方程为y-1=-(x-2),即x+y-3=0.
=4k2,即k=-1时取得最小值,此时直线l的方程为y-1=-(x-2),即x+y-3=0.
16.已知关于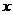 的一元二次函数
的一元二次函数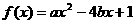 .
.
(1)设集合P={1,2, 3}和Q={-1,1,2,3,4},分别从集合P和Q中随机取一个数作为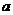 和
和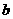 ,求函数
,求函数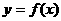 在区间[
在区间[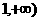 上是增函数的概率;
上是增函数的概率;
(2)设点(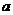 ,
,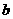 )是区域
)是区域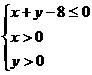 内的随机点,求
内的随机点,求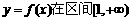 上是增函数的概率.
上是增函数的概率.
解:(1)∵函数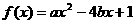 的图象的对称轴为
的图象的对称轴为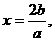
要使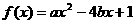 在区间
在区间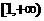 上为增函数,
上为增函数,
当且仅当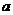 >0且
>0且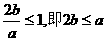
若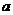 =1则
=1则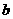 =-1, 若
=-1, 若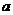 =2则
=2则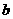 =-1,1; 若
=-1,1; 若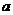 =3则
=3则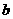 =-1,1;
=-1,1;
∴事件包含基本事件的个数是1+2+2=5∴所求事件的概率为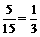 .
.
(2)由(Ⅰ)知当且仅当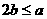 且
且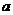 >0时,
>0时,
函数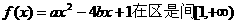 上为增函数,
上为增函数,
依条件可知试验的全部结果所构成的区域为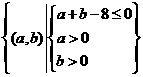
构成所求事件的区域为三角形部分. 由
∴所求事件的概率为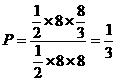 .
.
15. 某高校从参加今年自主招生考试的学生中随机抽取容量为50的学生成绩样本,得频率分布表如下:
|
组号 |
分组 |
频数 |
频率 |
|
第一组 |
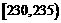 |
8 |
0.16 |
|
第二组 |
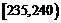 |
① |
0.24 |
|
第三组 |
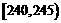 |
15 |
② |
|
第四组 |
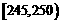 |
10 |
0.20 |
|
第五组 |
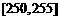 |
5 |
0.10 |
|
合
计 |
50 |
1.00 |
(1)写出表中①②位置的数据;
(2)为了选拔出更优秀的学生,高校决定在第三、四、五组中用分层抽样法抽取6名学生进行第二轮考核,分别求第三、四、五各组参加考核人数;
(3)在(2)的前提下,高校决定在这6名学生中录取2名学生,求2人中至少有1名是第四组的概率.
解: (1) ①②位置的数据分别为12、0.3; ……………………………4分
(2) 第三、四、五组参加考核人数分别为3、2、1;……………………8分
(3) 设上述6人为abcdef(其中第四组的两人分别为d,e),则从6人中任取2人的所有情形为:{ab,ac,ad,ae,af,bc,bd,be,bf,cd,ce,cf,de,df,ef}
共有15种.……………………………………………………………10分
记“2人中至少有一名是第四组”为事件A,则事件A所含的基本事件的种数有9种.………………………………………………………………………12分
所以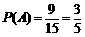 ,故2人中至少有一名是第四组的概率为
,故2人中至少有一名是第四组的概率为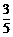 .………14分
.………14分
14.已知等比数列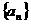 的首项为
的首项为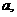 公比为
公比为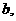 则点
则点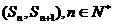 所在的定直线方程为_____________________答案:
所在的定直线方程为_____________________答案: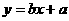
13. 直线l: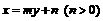 过点
过点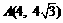 ,若可行域
,若可行域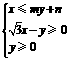 的外接圆的直径为
的外接圆的直径为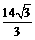 ,
,
则实数n的值为________________..答案: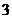 或
或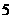
12.已知方程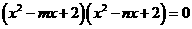 的四个根组成一个首项为
的四个根组成一个首项为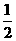 的等比数列,则
的等比数列,则
|m-n|= 答案: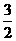
11.已知二次函数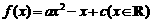 的值域为
的值域为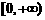 ,则
,则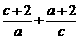 的最小值
的最小值
为 .答案:
10.如图,半径为8 cm的圆形纸板内有一个相同圆心的半径为1 cm的小圆.现将半径为1 cm的一枚硬币抛到此纸板上,使硬币整体随机落在纸板内,则硬币落下后与小圆无公共点的概率为
. 答案: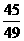
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com