22．

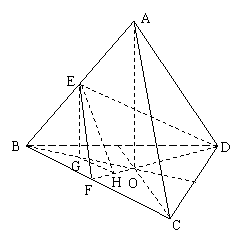
解：(Ⅰ)作AO⊥平面BCD于O,由正三棱锥的性质

可知O为底面中心，连CO,则CO⊥BD,由三垂线定理

知AC⊥BD，又AC⊥ED,∴AC⊥平面ABD,∴AC⊥AD,

AB⊥AC,AB⊥AD.在Rt△ACD中，由AC²+AD²=2AC²=a²

可得：AC=AD=AB=.

∴V=V_B-ACD=.

(Ⅱ)过E作EG⊥平面BCD于G，过G作GH⊥FD于H，连EH，由三垂线定理知EH⊥FD,即∠EHG为二面角E-FD-B的平面角.

∵EG＝AO 而AO＝,∴EG=.

又∵ED＝∵EF∥AC，∴EF⊥DE.∴在Rt△FED

中，EH＝∴在Rt△EGH中，sin∠EHG＝

21．

解：先求出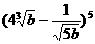的常数项是2⁷，从而可得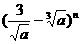中n=7，对于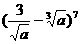由二项展开式的通项公式知，含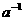的项是第4项，其二项式系数是35。

20．用0，1，2，3，4，5组成没有重复数字的自然数，

(1)　 119　　　 (2)　 21

19．

解(Ⅰ)延长ED交CB延长线于F，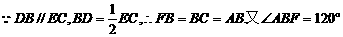

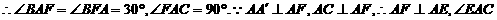为截

面与底面所成二面角的平面角.　 在Rt△AEC中，EC=AC，故得∠EAC=45°.

(Ⅱ)设AB=a，则，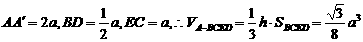

．

.

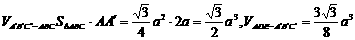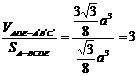
18．

　 [解]　 (1)用简单随机抽样，每个个体被抽到的概率为＝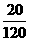

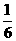
　　 用分层抽样：一、二、三级品被抽取数分别为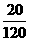×24＝4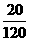，×36＝6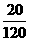，×60＝10。

故每层中每个个体被抽到的概率分别为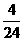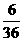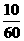，， 即都是。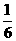

　(2)用分层抽样时，因为在一级品抽样与在二级品中抽样是独立的，故一级品甲与二级　 品乙都被抽到的概率为P＝·＝。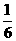

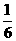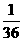　用简单随机抽样时一级品甲与二级品乙都被抽到的概率为

　　 P′＝＝×＜×=。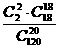

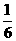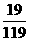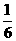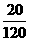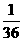　故用分层抽样时，一级品甲与二级品乙都被抽到的概率较大．

17． y=2x³－9x²+12x－4

22．已知正三棱锥A-BCD的边长为a，E、F分别为AB、BC的中点，且AC⊥DE.

(Ⅰ)求此正三棱锥的体积；

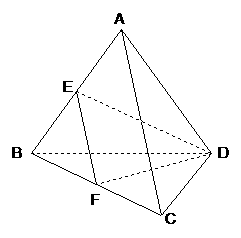(Ⅱ)求二面角E-FD-B的正弦值.

.

高二数学综合练习(四)答案

21．已知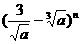的展开式的各项系数之和等于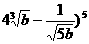展开式中的常数项，求 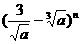展开式中含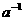的项的二项式系数。

20．用0，1，2，3，4，5组成没有重复数字的自然数，

(1)　 有多少个比201 345大？

(2)有多少个是25的倍数的四位数？

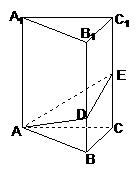
19．正三棱柱ABC-A₁B₁C₁中，AA₁=2AB，D、E分别是侧棱BB₁、CC₁上的点，且EC=BC=2BD，过A、D、E作一截面，求：

　 (Ⅰ)截面与底面所成的角；　 (Ⅱ)截面将三棱柱分成两部分的体积之比.