
题目列表(包括答案和解析)
7.用一个与圆柱母线成60度的平面截圆柱,截口是一个椭圆,这个椭圆的离心率是
A.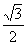 B.0.5
B.0.5
C.0.25 D.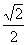
6.集点在(-1,0),顶点在(1,0)的抛物线方程是
A.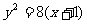
B.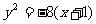
C.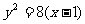
D.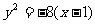
5.复数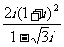 等于
等于
A.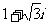 B.
B.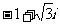
C.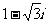 D.
D.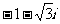
4.某个命题与自然数n有关,如果当n=k(k∈N)时该命题成立,那么可推出n=k+1时该命题也成立,现已知当n=100时该命题不成立,那么可以推得:
A.当n=101时该命题不成立
B.当n=101时该命题成立
C.当n=99时该命题不成立
D.当n=99时该命题成立
3.若a>b>0则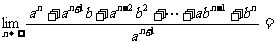
A.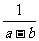 B.
B.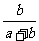
C.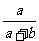 D.
D.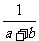
2.已知x、y是复数,
(1)若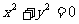 ,则x=y=0,
,则x=y=0,
(2)若xy=0,则x=0或y=0
(3)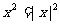 ,
,
(4)若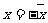 则x是纯虚数。
则x是纯虚数。
上面的命题中正确的命题的个数是
A.0 B.1 C.2 D.3
1.若用C、R和I分别表示复数集、实数集和纯虚数集,其中C为全集,则
A.C=R∪I B.R∩I={0}
C.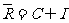 D.R∩I=ф
D.R∩I=ф
① 已知等比数列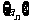 的公比为q >1,则
的公比为q >1,则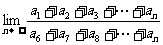 等于( )
等于( )
A) 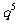 B)
B) 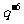 C) q D) 1
C) q D) 1
② 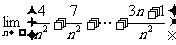 的值为( )
的值为( )
A) 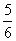 B)
B) 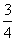 C)
C) 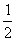 D)
D) 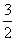
③ 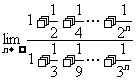 的值为
的值为
④ 
⑤ 若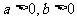 , 则
, 则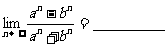
⑥ 已知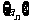 是以
是以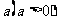 为首项以
为首项以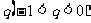 为公比的等比数列,设
为公比的等比数列,设
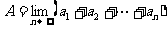
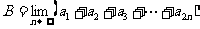
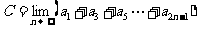
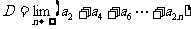
则A,B,C,D的大小关系
思考题:
已知数列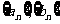 都是由正数组成的等比数列,公比分别为p, q其中
都是由正数组成的等比数列,公比分别为p, q其中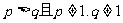 ,设
,设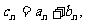 Sn为数列
Sn为数列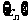 的前n项和.求
的前n项和.求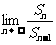 .
.
(97年全国高考题)
⑴只有无穷数列才可能有极限,有限数列无极限.
⑵运用数列极限的运算法则求数列极限应注意法则适应的前提条件.(参与运算的数列都有极限,运算法则适应有限个数列情形)
⑶求数列极限最后往往转化为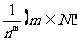 或
或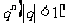 型的极限.
型的极限.
⑷求极限的常用方法:
①分子、分母同时除以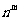 或
或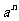 .
.
②求和(或积)的极限一般先求和(或积)再求极限.
③利用已知数列极限(如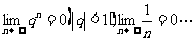 等).
等).
④含参数问题应对参数进行分类讨论求极限.
例1 求下列极限
①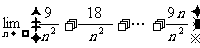
② 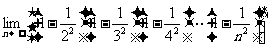 .
.
③ 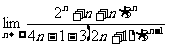 . ④
. ④ 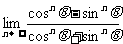
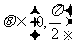 .
.
评析:1)四则运算法则只对任意有限个数列可进行四则运算,①小题数列个数是无限的,不适用于四则运算法则,因此应先求和后求极限.
2)对无穷多项的和(或积)求极限一般采用先求和(或积)后求极限.
3)分式的极限通常是分子分母同除以趋向 较快的项.
较快的项.
4)求解含参数式子的极限时,应注意对参数进行分类讨论.
例2
已知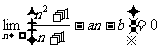 ,求实数a , b的值.
,求实数a , b的值.
评析:这是一个求待定常数的极限逆向问题,一般都是从求极限入手建立关于a, b的方程组求解
例3 数列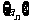 是首项为1,公比为
是首项为1,公比为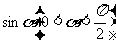 的等比数列,又
的等比数列,又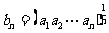 ,
,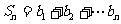 . 求
. 求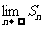
评析:求一个数列前n项和的极限主要是确定和的表达式.本题解题关键是先确定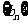 为等比数列,然后求和Sn的表达式,再求极限.
为等比数列,然后求和Sn的表达式,再求极限.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com