
题目列表(包括答案和解析)
学生课前练习:
⑴ 已知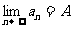 ,则在区间
,则在区间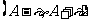 外(
外( 为任意小的正常数)这数列
为任意小的正常数)这数列 的项数为 (填“有限项”或“无穷项”)
的项数为 (填“有限项”或“无穷项”)
⑵ 下列命题正确的是( )
①数列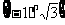 没有极限 ②数列
没有极限 ②数列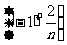 的极限为0
③数列
的极限为0
③数列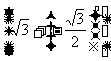 的极限为
的极限为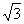 ④ 数列
④ 数列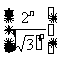 没有极限
没有极限
A ①② B ②③④ C ①②③ D ①②③④
⑶  的( )
的( )
A 充分必要条件 B 充分不必要条件
C 必要不充分条件 D 既不充分又不必要条件
⑷ 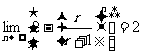 ,则r的取值范围是( )
,则r的取值范围是( )
A
-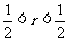 B
B 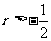 C
C 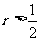 D
D 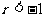
(5) 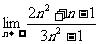 的值为( )
的值为( )
A -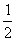 B -
B -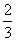 C
C 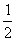 D
D 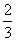
知识归纳:
1) 数列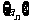 的极限定义:
的极限定义:
任给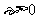 ,存在N>0,当n>N时,
,存在N>0,当n>N时,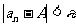 恒成立.记作
恒成立.记作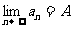 .
.
注意:①N与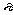 有关.②
有关.②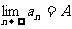 的几何意义是当n>N时,
的几何意义是当n>N时,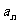 对应的点全部落在区间
对应的点全部落在区间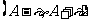 之内.
之内.
2) 数列极限的运算法则:如果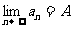 ,
, .则
.则
① 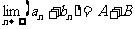 .②
.② 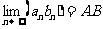 .③
.③ 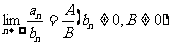 .
.
注意:和与积必须是有限的。
3) 几个常用极限:
① 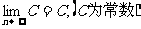 . ②
. ② 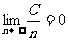 . ③
. ③ 
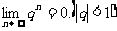 .
.
4) 两种基本类型的极限:①
② 
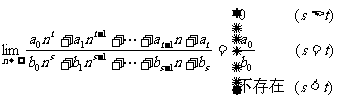
(17)在4与64之间插入三个正数a、b、c,使4,a,b与b,c,64都成等比数列,且使a,b,c成等差数列,求a、b、c的值.
(18)已知等差数列前三项为a,4,3a,前n项和为 ,
,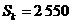 .
.
(Ⅰ)求a和k的值;
(Ⅱ)求数列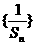 的前n项和
的前n项和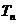 .
.
(19)数列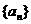 为正项的等比数列,它的前n项和为80,前2n项和为6 560,且在前n项中数值最大的项为54.求这等比数列的首项
为正项的等比数列,它的前n项和为80,前2n项和为6 560,且在前n项中数值最大的项为54.求这等比数列的首项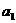 与公比q.
与公比q.
(20)已知a 、b 、g 都是锐角,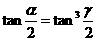 ,且2tanb =tang ,求证:a ,b ,g 成等差数列.
,且2tanb =tang ,求证:a ,b ,g 成等差数列.
(21)在等比数列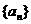 中,
中,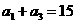 ,前4项和为45.设
,前4项和为45.设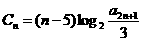 ,试问数列
,试问数列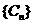 中有没有最小值?若有,求出这最小项,并指明项数;若没有,说明理由.
中有没有最小值?若有,求出这最小项,并指明项数;若没有,说明理由.
(22)假设A型进口汽车关税税率在2001年是100%,在2006年是25%,2001年A型进口车每辆价格为64万元(其中含32万元关税税款).
(Ⅰ)已知与A型进口车性能相近的B型国产车,2001年每辆价格为46万元.若A型车的价格只受关税降低的影响,为了保证2006年B型车的价格不高于A型车价格的90%,B型车价格要逐年降低,问平均每年至少下降多少万元?
(Ⅱ)某人在2001年将33万元存入银行,假设该银行扣利息税后的年利率为1.8%(五年内不变),且每年按复利计算(例如,第一年的利息计入第二年的本金),那么五年到期时这笔钱连本带息是否一定够买一辆按(Ⅰ)中所述降价后的B型汽车?
(13)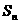 是等差数列
是等差数列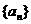 的前n项和,且
的前n项和,且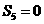 ,
,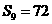 ,则
,则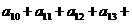
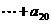 =__________.
=__________.
(14)在10到2000之间形如 的各数的和为__________.
的各数的和为__________.
(15)数列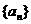 中,
中,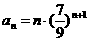 ,则此数列的最大项为__________.
,则此数列的最大项为__________.
(16)已知数列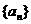 满足
满足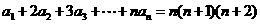 ,那么数列
,那么数列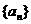 的前n项和的公式为
的前n项和的公式为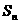 =__________.
=__________.
(1)在数列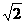 ,
,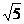 ,
,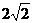 ,
,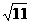 ,…中,如果
,…中,如果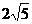 是这个数列中的一项,那么它的项数是( ).
是这个数列中的一项,那么它的项数是( ).
A.6 B.7 C.10 D.11
(2)数列0,2,0,2,…的通项为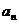 ,下列公式不能作为已知数列的通项公式的是( ).
,下列公式不能作为已知数列的通项公式的是( ).
A.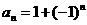 B.
B.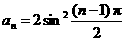
C.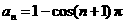 D.
D.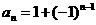
(3)已知数列{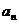 }中,
}中,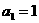 ,
,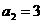 ,且
,且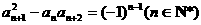 ,那么
,那么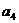 等于( ).
等于( ).
A.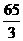 B.21
C.17
D.10
B.21
C.17
D.10
(4)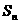 是数列
是数列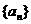 的前n项和,且
的前n项和,且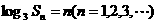 ,那么数列
,那么数列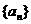 ( ).
( ).
A.是公比为3的等比数列 B.是公差为3的等差数列
C.是公比为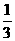 的等比数列 D.既非等差数列也非等比数列
的等比数列 D.既非等差数列也非等比数列
(5)等差数列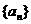 中,
中,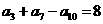 ,
,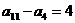 ,那么它的前13项和为( ).
,那么它的前13项和为( ).
A.168 B.156 C.78 D.152
(6)等比数列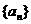 中,
中,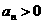 ,且
,且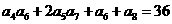 ,则
,则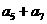 等于( ).
等于( ).
A.6 B.12 C.18 D.24
(7)数列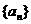 中,
中,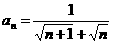 ,若其前n项和
,若其前n项和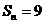 ,则n等于( ).
,则n等于( ).
A.9 B.10 C.99 D.100
(8)若a,b,c成等比数列,a,m,b成等差数列,n是b,c的等差中项,则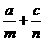 的值为( ).
的值为( ).
A.4 B.3 C.2 D.1
(9)数列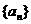 中,已知
中,已知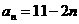 ,记
,记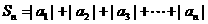 ,那么
,那么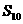 等于( ).
等于( ).
A.25 B.50 C.100 D.150
(10)等比数列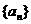 中,其前n项和为
中,其前n项和为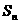 ,且
,且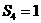 ,
,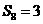 ,则
,则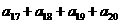 的值为( ).
的值为( ).
A.14 B.16 C.18 D.20
(11)在50到350之间的所有个位数字是1的整数的和为( ).
A.5 880 B.5 539 C.5 208 D.4 877
(12)现有200根相同的钢管,把它们堆放成正三角形垛,要使剩余钢管尽可能少,那么剩余钢管的根数为( ).
23. (本题9分)
 已知函数y=f(x)的定义域为[-1,1],且f(x)在[-1,1]上为增函数,又
已知函数y=f(x)的定义域为[-1,1],且f(x)在[-1,1]上为增函数,又
f(1)=1
(1)解不等式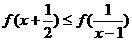 ;
;
(2)若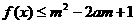 对于所有x∈[-1,1],a∈[-1,1]恒成立,求
对于所有x∈[-1,1],a∈[-1,1]恒成立,求
22. (本题8分)
设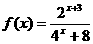
(1)求f(x)的最大值;
(2)证明:对于任意实数a,b恒有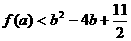

21. (本题8分)
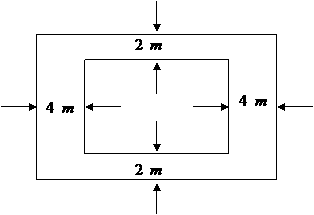
某校要建一个面积为392 m2的长方形游泳池,并且在四周要修建出宽为2 m和4 m的小路(如图所示)。问游泳池的长和宽分别为多少米时,占地面积最小?并求出占地面积的最小值。
20. (本题8分)
已知|a|<1,|b|<1且a≠b,求证: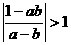
19. (本题8分)
已知a,b∈R,求证: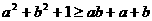
18.(本题8分)
解关于x的不等式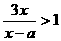 (a∈R)
(a∈R)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com