
题目列表(包括答案和解析)
3.动点P到x轴,y轴的距离之比等于非零常数k,则动点P的轨迹方程是( )
A.y=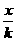 (x≠0) B.y=kx(x≠0)
(x≠0) B.y=kx(x≠0)
C.y=-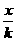 (x≠0) D.y=±kx(x≠0)
(x≠0) D.y=±kx(x≠0)
2.若点M到x轴的距离和它到直线y=8的距离相等,则点M的轨迹方程是( )
A.x=-4 B.x=4 C.y=-4 D.y=4
1.曲线f(x,y)=0关于直线x-y-2=0时称曲线的方程为( )
A.f(y+2,x)=0 B.f(x-2,y)=0
C.f(y+2,x-2)=0 D.f(y-2,x+2)=0
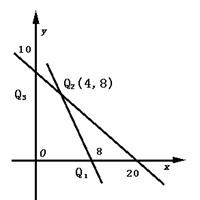
21.设x,y分别为甲、乙二种柜的日产量,可将此题归纳为如下线性规划模型fmax=20x+24y
其中 由图及下表
由图及下表
|
(x,y) |
f=20x+24y |
|
(0,10) |
240 |
|
(0,0) |
0 |
|
(8,0) |
160 |
|
(4,8) |
72 |
∴fmax=272
答:该公司安排甲、乙二种柜的日产量分别为4台和8台可获最大利润272元.
20.略 解:x-7y+19=0或7x+y-17=0
19.设过已知圆交点的圆系方程为:x2+y2-4x+2y+λ(x2+y2-2y-4)=0(λ≠-1),即(1+λ)x2+(1+λ)y2-4x+(2-2λ)y-4λ=0
圆心(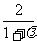 -
-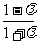 )又圆心在直线2x+4y=1上
)又圆心在直线2x+4y=1上
∴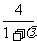
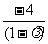 =1,∴λ=
=1,∴λ=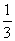
所求圆的方程为:x2+y2-3x+y-1=0
18.设直线L的方程为y=kx+b.A(x1,y1),B(x2,y2),M(x,y)由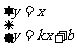 得A(
得A(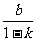 ,
,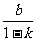 ),(k≠0)
),(k≠0)
由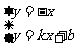 得B(
得B(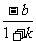 ,
,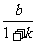 ),∴
),∴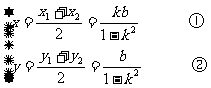
由①②得:k=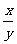 ,b=
,b=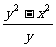 ③
③
∵圆C与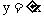 都相切
都相切
∴圆C的半径r=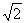 .
.
∵AB:kx-y+b=0与圆C相切,
∴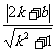 =
= 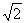 ,即2k2+4kb+b2-=0 ④
,即2k2+4kb+b2-=0 ④
将③代入④ (y2-x2)+4x(y2-x2)-2(y2-x2)=0
∵y2≠x2,∴y2-x2+4x-2=0即(x-2)2-y2=2.(y≠0)
当L⊥x轴时,线段AB的中点M(2±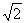 ,0)也合上面的方程,其轨迹在∠AOB内
,0)也合上面的方程,其轨迹在∠AOB内
17.设所求圆的圆心是C(a,b),则过m,c的直线与x+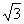 y=0垂直
y=0垂直
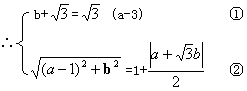
由①②可得,a=0,b=-4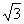 或a=4,b=0相应半径为6和2.
或a=4,b=0相应半径为6和2.
∴圆的方程为:x2+(y+4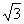 )2=36或(x-4)2+y2=4.
)2=36或(x-4)2+y2=4.
AA级
21.某家俱公司生产甲、乙两种型号的组合柜,每种柜的制造白坯时间、油漆时间及有关数据如下:(10′)
|
工艺要求 |
产品甲 |
产品乙 |
生产能力/(台/天) |
|
制白坯时间/天 |
6 |
12 |
120 |
|
油漆时间/天 |
8 |
4 |
64 |
|
单位利润/元 |
20 |
24 |
|
第七单元达纲检测(A级)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com