
题目列表(包括答案和解析)
1、直线l的倾斜角为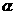 ,且
,且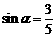 ,则直线l的斜率是
,则直线l的斜率是
A.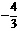 B.
B.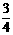 C.
C.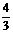 或
或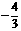 D.
D.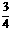 或
或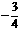
20.(本小题满分12分)
如图所示的多面体是由底面为ABCD的长方体被截面AEC1F所截面而得到的,其中AB=4,BC=2,CC1=3,BE=1.
(Ⅰ)求BF的长;
(Ⅱ)求点C到平面AEC1F的距离.
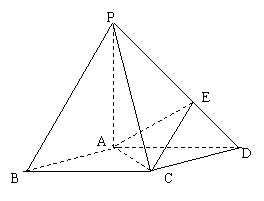
19、如图,在底面是菱形的四棱锥P-ABCD中,∠ABC=600,PA=AC=a,PB=PD=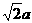 ,点E在PD上,且PE:ED=2:1.
,点E在PD上,且PE:ED=2:1.
(I)证明PA⊥平面ABCD;
(II)求以AC为棱,EAC与DAC为面的二面角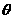 的大小;
的大小;
(Ⅲ)在棱PC上是否存在一点F,使BF//平面AEC?证明你的结论.
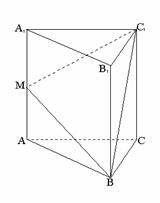
18、 如图,在正三棱柱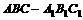 中,
中,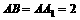 ,由顶点B沿棱柱侧面经过棱
,由顶点B沿棱柱侧面经过棱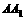 到顶点
到顶点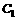 的最短路线与
的最短路线与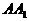 的交点记为M,求:
的交点记为M,求:
(I)求证:平面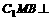 平面
平面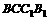
(II)平面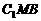 与平面ABC所成二面角(锐角)的大小
与平面ABC所成二面角(锐角)的大小
17.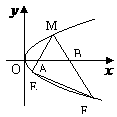 如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
如图,M是抛物线上y2=x上的一点,动弦ME、MF分别交x轴于A、B两点,且MA=MB.
(1)若M为定点,证明:直线EF的斜率为定值;
(2)若M为动点,且∠EMF=90°,求△EMF的重心G的轨迹
16、已知双曲线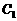 和椭圆
和椭圆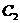 :
: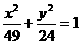 有公共的焦点,它们的离心率分别是
有公共的焦点,它们的离心率分别是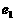 和
和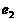 ,且
,且 ,求双曲线
,求双曲线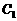 的方程.
的方程.
15、设有编号为1,2,3,4,5的五个球和编号为1,2,3,4,5的五个盒子,现将这五个球放入5个盒子内
(1)只有一个盒子空着,共有多少种投放方法?
(2)没有一个盒子空着,但球的编号与盒子编号不全相同,有多少种投放方法?
(3)每个盒子内投放一球,并且至少有两个球的编号与盒子编号是相同的,有多少种投放方法?
14、正方形ABCD的两对角线AC与BD交于O,沿对角线BD折起,使∠AOC=90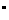 对于下列结论:①AC⊥BD;②△ADC是正三角形;③AB与CD成60
对于下列结论:①AC⊥BD;②△ADC是正三角形;③AB与CD成60 角;④AB与平面BCD成60
角;④AB与平面BCD成60 角,其中正确的结论是_____________________。
角,其中正确的结论是_____________________。
13、直线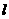 的方程为
的方程为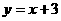 ,在
,在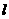 上任取一点P,若过点P且以双曲线
上任取一点P,若过点P且以双曲线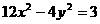 的焦点作为椭圆的焦点,那么具有最短长轴的椭圆方程为________________________。
的焦点作为椭圆的焦点,那么具有最短长轴的椭圆方程为________________________。
12、已知正方体的棱长为1,则过A1C1且与BD1平行的截面面积为___________。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com