
题目列表(包括答案和解析)
2.将三棱锥P-ABC(如图甲),沿三条侧棱剪开后,展开成如图乙的形状,其中P1、B、P2共线,P2、C、P3共线,且P1P2 = P2P3,则在三棱锥P-ABC中,PA与BC所成的角是( )
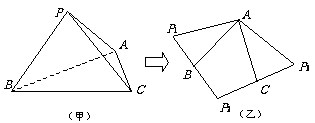 A.30°
B.45°
A.30°
B.45°
C.60° D.90°
1. ABCD-A1B1C1D1是单位正方体,黑白两个蚂蚁从点A出发沿棱爬行,每走完一条棱称为“走完一段”。白蚂蚁爬行的路线是AA1→A1D1→…,黑蚂蚁爬行的路线是AB→BB1→…,它们都遵循如下规则:所爬行的第i+2段与第i段所在直线必须是异面直线(其中i∈N+),设两蚂蚁都走完第2003段后分别停在正方体的一个顶点处,则黑白蚂蚁的距离是 ( )
A.1 B. C. D.0
21.设函数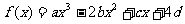 (a、b、c、d∈R)图象关于原点对称,且x=1时,
(a、b、c、d∈R)图象关于原点对称,且x=1时,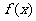 取极小值
取极小值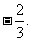 (1)求a、b、c、d的值;(2)当
(1)求a、b、c、d的值;(2)当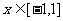 时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;(3)若
时,图象上是否存在两点,使得过此两点处的切线互相垂直?试证明你的结论;(3)若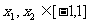 时,求证:
时,求证: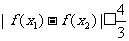 .
.
20.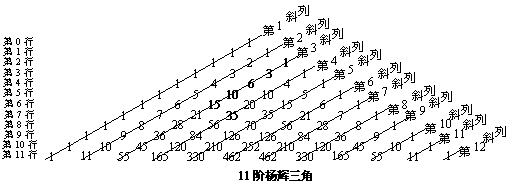 杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共五种二十一卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下面是一个11阶的杨辉三角:
杨辉是中国南宋末年的一位杰出的数学家、数学教育家.他的数学著作颇多,他编著的数学书共五种二十一卷,在他的著作中收录了不少现已失传的古代数学著作中的算题和算法.他的数学研究与教育工作的重点是在计算技术方面.杨辉三角是杨辉的一大重要研究成果,它的许多性质与组合数的性质有关.杨辉三角中蕴涵了许多优美的规律.古今中外,许多数学家如贾宪、朱世杰、帕斯卡、华罗庚等都曾深入研究过,并将研究结果应用于其他工作.下面是一个11阶的杨辉三角:
试回答:(其中第(1)~(4)小题只须直接给出最后的结果,无须求解过程.)
(1)记第i(i∈N*)行中从左到右的第j(j∈N*)个数为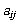 ,则数列{
,则数列{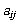 }的通项公式为
;n阶杨辉三角中共有
个数.
}的通项公式为
;n阶杨辉三角中共有
个数.
(2)第k行各数的和是 .
(3)n阶杨辉三角的所有数的和是 .
(4)第p(p∈N*,且p≥2)行除去两端的数字1以外的所有数都能被p整除,则整数p一定为 .A.奇数 B.质数 C.非偶数 D.合数
(5)在第3斜列中,前5个数依次为1、3、6、10、15;第4斜列中,第5个数为35.显然,1+3+6+10+15=35.事实上,一般地有这样的结论:
第m斜列中(从右上到左下)前k个数之和,一定等于第m+1斜列中第k个数.
试用含有m、k(m、k∈N*)的数学公式表示上述结论并证明其正确性.
数学公式为: .
19. 甲、乙、丙三台机床各自独立地加工同一种零件,已知甲机床加工的零件是一等品而乙机床加工的零件不是一等品的概率为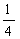 ,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为
,乙机床加工的零件是一等品而丙机床加工的零件不是一等品的概率为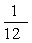 ,甲、丙两台机床加工的零件都是一等品的概率为
,甲、丙两台机床加工的零件都是一等品的概率为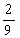 .(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率。
.(Ⅰ)分别求甲、乙、丙三台机床各自加工零件是一等品的概率;(Ⅱ)从甲、乙、丙加工的零件中各取一个检验,求至少有一个一等品的概率。
18.如图,在斜三棱柱ABC-A1B1C1 中,侧面AA1B1B⊥底面ABC,侧棱AA1与底面ABC成600的角, AA1= 2.底面ABC是边长为2的正三角形,其重心为G点。E是线段BC1上一点,且BE=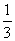 BC1 .(1)求证: GE∥侧面AA1B1B ;(2)求平面B1GE与底面ABC所成锐二面角的大小 .
BC1 .(1)求证: GE∥侧面AA1B1B ;(2)求平面B1GE与底面ABC所成锐二面角的大小 .
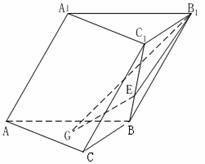
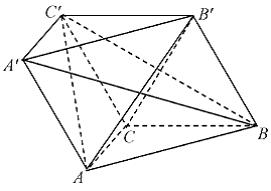
17.在三棱柱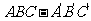 中,侧面
中,侧面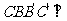 底面
底面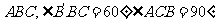 ,且
,且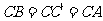 .(1)求证:平面
.(1)求证:平面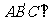 平面
平面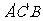 ;(2)求异面直线
;(2)求异面直线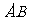 与
与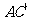 所成的角。
所成的角。
16.设函数f(x)=k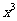 +3(k-1)
+3(k-1)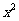
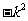 +1在区间(0,4)上是减函数,则k的取值范围是 .
+1在区间(0,4)上是减函数,则k的取值范围是 .
15.有一组数据: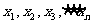
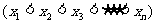 的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数
的算术平均值为10,若去掉其中最大的一个,余下数据的算术平均值为9;若去掉其中最小的一个,余下数据的算术平均值为11,第一个数 关于
关于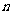 的表达式是__________,第
的表达式是__________,第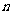 个数
个数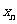 关于
关于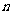 的表达式是___________.
的表达式是___________.
14.从装有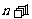 个球(其中
个球(其中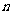 个白球,1个黑球)的口袋中取出
个白球,1个黑球)的口袋中取出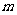 个球
个球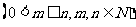 ,共有
,共有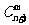 种取法。在这
种取法。在这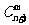 种取法中,可以分成两类:一类是取出的
种取法中,可以分成两类:一类是取出的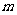 个球全部为白球,共有
个球全部为白球,共有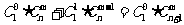 ,即有等式:
,即有等式: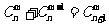 成立。试根据上述思想化简下列式子:
成立。试根据上述思想化简下列式子: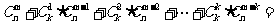 .
.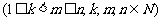 .
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com