
题目列表(包括答案和解析)
19、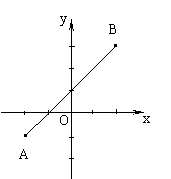 如图,已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围.
如图,已知点A(-2,-1)和B(2,3),圆C:x2+y2 = m2,当圆C与线段AB没有公共点时,求m的取值范围.
解:∵过点A、B的直线方程为在l:x-y+1 = 0 ……2分
作OP垂直AB于点P,连结OB
由图象得:|m|<OP或|m|>OB时,线段AB与圆x2+y2 = m2无交点. ……………2分
(I)当|m|<OP时,由点到直线的距离公式得:
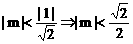 ,即
,即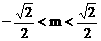 .
……………3分
.
……………3分
(II)当m>OB时
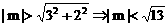 即
即 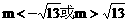 . ………………3分
. ………………3分
∴当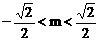 和
和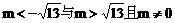 时,圆x2+y2 = m2与线段AB无交点。 ………2分
时,圆x2+y2 = m2与线段AB无交点。 ………2分
18、已知直线l1: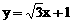 ,直线l2经过点P(0,1),且l2到l1的角为30º,求直线l2的方程.
,直线l2经过点P(0,1),且l2到l1的角为30º,求直线l2的方程.
解:已知直线l1的斜率为k1=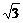 ,设直线l2的方程为y=k2x+b,
,设直线l2的方程为y=k2x+b,
∵k1=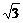 ,∴l1的倾斜角为60º,
,∴l1的倾斜角为60º,
又l2到l1的角为30º,∴0<k2<k1,且l1与l2的夹角是30º ……………2分
∴tanα=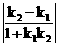 ,∴tan30º=
,∴tan30º=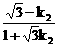
解之得:k2=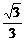 …………5分
…………5分
∵直线l2经过点P(0,1),∴b=1 ……………2分
∴直线l2的方程为y=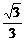 x+1
…………1分
x+1
…………1分
17、(1)已知x、y、z∈R,且x+y+z=a,求证:x2+y2+z2≥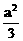
(2)已知a<0,求1-2a-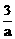 的最值.
的最值.
(1)证明:∵x+y+z=a,∴x2+y2≥2xy,y2+z2≥2yz,x2+z2≥2xz …………3分
∵x+y+z=a,∴a2=(x+y+z)2= x2+y2+z2+2xy+2yz+2xz≤3(x2+y2+z2) ………3分
∴x2+y2+z2≥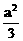 ………2分
………2分
(2)解:当a<0时,-2a>0,-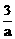 >0,
………2分
>0,
………2分
∵(-2a)(-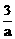 )=6为定值
…………2分
)=6为定值
…………2分
又∵当且仅当-2a=-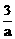 ,即a=
,即a= 时,-2a-
时,-2a-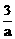 有最小值为
有最小值为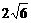
∴1-2a-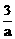 有最小值为1+
有最小值为1+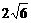 ………4分
………4分
16、对于椭圆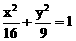 和双曲线
和双曲线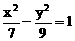 有下列命题:
有下列命题:
①椭圆的焦点恰好是双曲线的顶点;
②双曲线的焦点恰好是椭圆的顶点;
③双曲线与椭圆共焦点;
④椭圆与双曲线有两个顶点相同.
其中正确命题的序号是①②
15、抛物线y=x2上到2x-y=4距离最近的点的坐标是(1,1)
13、过点(1,1)圆(x-1)2+(y-2)2 = 1的切线方程是y =1
翰林汇14、等腰三角形ABC的底边的两个顶点是B(2,4)和C(3,-5),则顶点A的轨迹方
程为x-9y-7=0 (x≠)
12、如果椭圆的两条准线间的距离是这个椭圆的焦距的两倍,那么这个椭圆的离心率为
A、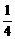 B、
B、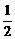 C、 D、
C、 D、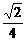
11、参数方程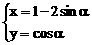 (α为参数)所表示的曲线是:
(α为参数)所表示的曲线是:
A、圆 B、椭圆 C、直线 D、抛物线的一部分
8、 方程x=
方程x=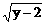 +1的曲线是
+1的曲线是
A B C D
翰林汇翰林汇9、下列各点中不在曲线上x2+y2-2mx+2my=0(m≠0)上的点是
A、(0,2m) B、(0,-2m) C、(2m,0) D、(0,0)
10翰林汇、在直角坐标系中,与两坐标轴都相切的圆的圆心轨迹方程是
A、y=x B、y=|x|(x≠0) C、x2-y2=0 D、x2-y2=0(x≠0)
7、若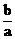 <-1,则方程bx2-ay2=b的曲线是
<-1,则方程bx2-ay2=b的曲线是
A、焦点在x轴上的椭圆 B、焦点在x轴上的双曲线
C、焦点在y轴上的椭圆 D、焦点在y轴上的双曲线翰林汇
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com