
题目列表(包括答案和解析)
(21)过抛物线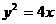 的焦点作直线与此抛物线相交于两点P和Q,求线段PQ中点的轨迹方程。
的焦点作直线与此抛物线相交于两点P和Q,求线段PQ中点的轨迹方程。
(22)已知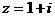 ,且
,且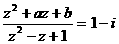 ,求实数a、b的值。
,求实数a、b的值。
(23)已知椭圆的率心率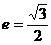 且左焦点与左准线分别为抛物线
且左焦点与左准线分别为抛物线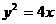 的焦点和准线,求此椭圆方程。
的焦点和准线,求此椭圆方程。
(24)数列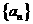 中,已知
中,已知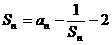 ,
,
①求出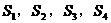 。
。
②猜想数列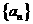 的前n项和
的前n项和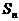 的公式,并加以证明。
的公式,并加以证明。
③求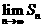 的值。
的值。
(25)已知双曲线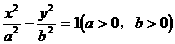 ,过右焦点F作第一、三象限的渐近线的垂线
,过右焦点F作第一、三象限的渐近线的垂线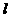 ,垂足为P,且
,垂足为P,且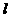 在双曲线左右两支的交点为A、B。
在双曲线左右两支的交点为A、B。
①求证:点P在双曲线的右准线上。
②求双曲线离心率的取值范围。

(16)已知a、b、c成等比数列,公比为3,且a、b+8、c成等差数列,则b=_____。
(17)计算机的成本不断降低,若每隔5年价格降低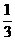 ,现在价格8100元,计算机15年后的价格为__________。
,现在价格8100元,计算机15年后的价格为__________。
(18)在等比数列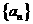 中,
中,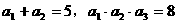 ,则
,则
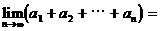 _______。
_______。
(19)双曲线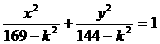 的焦距是___________。
的焦距是___________。
(20)顶点在原点,焦点在x轴的负半轴上的抛物线被直线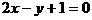 截得的弦长为
截得的弦长为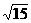 ,则抛物线方程是__________________。
,则抛物线方程是__________________。
(1)等差数列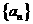 中,
中,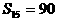 ,则
,则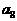 的值为( )
的值为( )
A. 3 B. 4 C. 6 D. 12
(2)设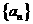 是公差为-2的等差数列,如果
是公差为-2的等差数列,如果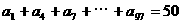 ,则
,则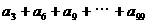 等于( )
等于( )
A. 182 B. -82 C. -80 D. 180
(3)抛物线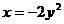 的准线方程是( )
的准线方程是( )
A. 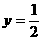 B.
B.
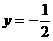 C.
C.
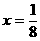 D.
D.
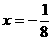
(4)一动圆与两圆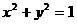 和
和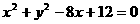 都外切,则动圆圆心轨迹为( )
都外切,则动圆圆心轨迹为( )
A. 圆 B. 椭圆 C. 双曲线的一支 D. 抛物线
(5)若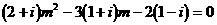 ,则实数m等于( )
,则实数m等于( )
A. 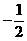 B.
B.
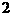 C.
C.
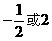 D.
1或2
D.
1或2
(6)若将20,50,100各加上相同的常数,组成等比数列,则其公比为( )
A. 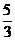 B.
B.
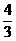 C.
C.
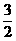 D.
D.
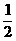
(7)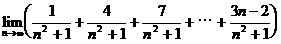 ( )
( )
A. 0 B.
1 C.
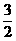 D.
3
D.
3
(8)一个等比数列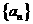 中,
中,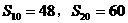 ,则
,则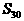 等于( )
等于( )
A. 183 B. 108 C. 75 D. 63
(9)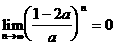 ,则
,则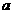 的取值范围是( )
的取值范围是( )
A. 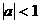 B.
B.
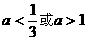
C. 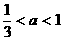 D.
D.
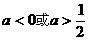
(10)椭圆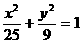 的两焦点
的两焦点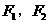 ,过
,过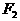 引直线L交椭圆于A、B两点,则
引直线L交椭圆于A、B两点,则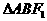 的周长为( )
的周长为( )
A. 5 B. 15 C. 10 D. 20
(11)若抛物线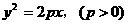 与
与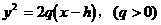 有公共焦点则( )
有公共焦点则( )
A. 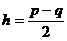 B.
B.
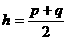
C. 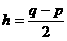 D.
D.
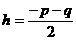
(12)到A(-1,0)和直线x=3的距离相等的点的轨迹方程为( )
A. 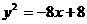 B.
B.
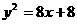
C. 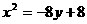 D.
D.
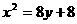
(13)若z为复数且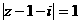 ,则
,则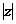 的最大值为( )
的最大值为( )
A. 1 B.
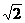 C.
C.
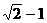 D.
D.
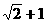
(14)若椭圆的短轴、焦距、长轴的长度依次成等差数列,则这个椭圆的离心率为( )
A. 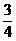 B.
B.
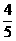 C.
C.
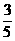 D.
D.
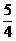
(15)已知双曲线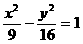 的右焦点为F,点A(9,2),在双曲线上有一点M,使
的右焦点为F,点A(9,2),在双曲线上有一点M,使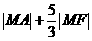 的值最小,则最小值是( )
的值最小,则最小值是( )
A. 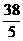 B.
B.
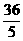 C
C
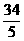 D.
D.
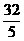
(17)(本小题满分12分)已知抛物线的顶点在原点,焦点在y轴的负半轴上, 且抛物线上一点P(m , -3 )到焦点F的距离为5. 求这个抛物线的方程.
(18)(本小题满分12分)解不等式:
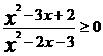
(19)(本小题满分12分)
要将两种大小不同的钢板截成A ,B ,C 三种规格,每张钢板可同时截得三种规格的小钢板的块数如下表所示:
|
规格类型 钢板类型 |
A规格 |
B规格 |
C规格 |
|
第一种钢板 |
2 |
1 |
1 |
|
第二种钢板 |
1 |
2 |
3 |
今需要A ,B ,C三种规格的成品分别为15 ,18 ,27 块,问各截这两种钢板多少张可得所需三种规格成品,且使所用钢板张数最少.
(20)(本小题满分12分)已知 a > 0 , b > 0 , 2c > a + b.求证
c - 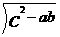 < a < c +
< a < c +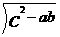 .
.
(21)(本小题满分14分)已知椭圆 C1 :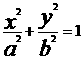 ( a > b > 0 )的一条准线方程是 x =
( a > b > 0 )的一条准线方程是 x =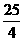 ,其左 ,右顶点分别是
A , B ;双曲线 C2
,其左 ,右顶点分别是
A , B ;双曲线 C2 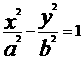 的一条渐近线方程为 3x – 5y = 0 .
的一条渐近线方程为 3x – 5y = 0 .
(1)求椭圆 C1的方程和双曲线C2的离心率 ;
(2)在第一象限内取双曲线C2上一点P ,连接AP交椭圆C1于点M ,连接PB并延长交椭圆C1于点N ,若点M恰为线段AP的中点, 求证MN  ┷ AB .
┷ AB .
(22)(本小题满分12分, 附加题8分)
(Ⅰ)某小区欲建一面积为640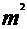 的距形绿地,四周有小路,绿地长边外小路宽5m ,短边外小路宽8m ,怎样设计绿地的长宽使绿地和小路总占地面积最小?
的距形绿地,四周有小路,绿地长边外小路宽5m ,短边外小路宽8m ,怎样设计绿地的长宽使绿地和小路总占地面积最小?
(Ⅱ) (附加题, 答对加8分,但全卷总分不超过150分)
如果将640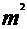 改为a
改为a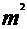 (300
(300  a
a  ), 并界定绿地长边至多28m
,至少20m .
), 并界定绿地长边至多28m
,至少20m .
怎样设计绿地的长宽使绿地和小路总占地面积最小?
(13)电影放映机的聚光灯有一个反射镜,它的形状是旋转椭圆面.为了使片门(电影胶片通过的地方)处获得最强光线,灯丝与片门应位于椭圆的两个焦点处,这是利用___________的一个实例.
(14)如果a,b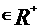 ,且a≠b,则
,且a≠b,则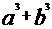 与
与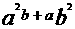 的大小关系是___________.
的大小关系是___________.
(15)与两圆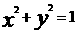 及
及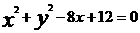 都外切的圆的圆心在_____________上.
都外切的圆的圆心在_____________上.
(16)若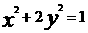 ,则
,则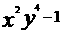 的最大值是____.
的最大值是____.
(1)直线的倾斜角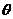 的取值范围是( ) .
的取值范围是( ) .
A . 0 <
<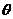 <
<
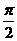 B . 0
B . 0 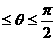 C .0
C .0 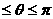 D .0
D .0 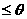 <
<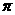
(2)方程{
x = a
+ r cos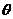
y = b
+ r sin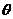 (
( 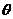 为参数 )表示的曲线是 (
).
为参数 )表示的曲线是 (
).
A .椭圆 B.圆 C.双曲线 D.抛物线
(3)等轴双曲线的离心率等于( ).
A. 1
B. 2 C.
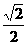 D.
D.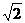
(4)给出下列四个命题:
①如果a > b,那么a – c > b – c ;②如果a > b ,那么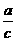 >
>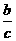

③如果a > b, c > d,那么ac >bd;④如果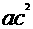 >
> 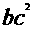 ,那么a>b.
,那么a>b.
其中真命题的个数为( ).
A.1 B. 2 C. 3 D. 4
(5)椭圆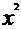 +2
+2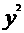 =4的准线方程是 ( ).
=4的准线方程是 ( ).
A.x=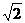 ,x=-
,x=-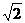 B.x=
B.x=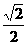 ,x=-
,x=-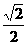
C.x=2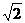 ,x=-2
,x=-2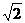 D.x=
D.x=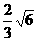 ,x=-
,x=-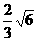
(6)若a=2-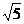 ,b=
,b=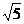 -2,c=5-2
-2,c=5-2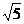 ,则 ( ).
,则 ( ).
A. b<a<c B.a<c<b C.c<a<b D.a<b<c
(7)双曲线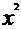 -
-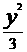 =-1的焦点坐标是 ( ).
=-1的焦点坐标是 ( ).
A.(0 ,2),(0 ,-2) B.(2 ,0),(-2,0)
C.(0 ,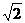 ),(0 ,-
),(0 ,-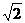 ) D.(0, 4),(0,-4)
) D.(0, 4),(0,-4)
(8)若直线(1+a)x+y+1=0与圆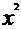 +
+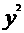 -2x=0相切,则a的值为( ).
-2x=0相切,则a的值为( ).
A.1,-1 B.2 ,- 2 C.1 D.-1
(9)椭圆5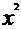 +k
+k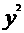 =5的一个焦点是(0,2),则k=( ).
=5的一个焦点是(0,2),则k=( ).
A.-1 B.1 C.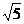 D.-
D.-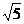 (10)若a>b>1,P=
(10)若a>b>1,P=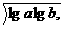 Q=
Q=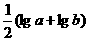 ,R=lg(
,R=lg(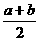 )
)
则 ( ).
A.R<P<Q B.P<Q<R C.Q<P<R D.P<R<Q
(11)已知两条直线l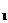 :y = x, l
:y = x, l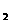 : ax –y = 0,其中a 为实数,当这两条直线的夹角在(0 ,
: ax –y = 0,其中a 为实数,当这两条直线的夹角在(0 ,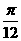 )变动时,a的取值范围是( ).
)变动时,a的取值范围是( ).
A.(0
,-1) B.(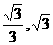 ) C.
(
) C.
(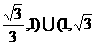 ) D.
(1,
) D.
(1, 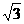 )
)
(12)过抛物线y =2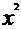 的焦点F作一直线,交抛物线与M , N两点.若线段MF 与FN 的长分别是m ,n,则
的焦点F作一直线,交抛物线与M , N两点.若线段MF 与FN 的长分别是m ,n,则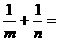 ( ).
( ).
A.4 B.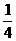 C.8 D.2
C.8 D.2
4. 求经过直线x=-2与已知圆x2+y2+2x-4y-11=0的交点的所有圆中,具有最小面积的圆的方程。
3. 自点P(-3,3)发出的光线l经x轴反射,其反射线所在直线正好与圆x2+y2-4x-4y+7=0相切,求光线l所在直线的方程。
1. 已知:x、y满足x+3y-10=0,则x2+y2的最小值为______________
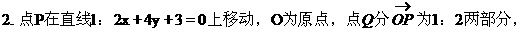 求动点Q的轨迹方程。
求动点Q的轨迹方程。
3. 过点P(2,4),作圆(x-1)2+(y-1)2=1的切线,则圆的切线方程是______________。
解:1. 判断直线与圆的位置关系,应看圆心到直线的距离与圆的半径的大小关系即可。
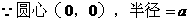


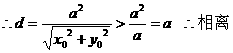
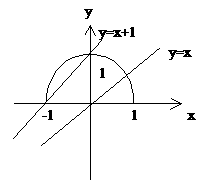
解:2. 数形结合为最佳方法:
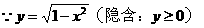
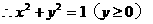
y=x+b表示一簇与y=x平行的直线,当y=x向上运动到b=1时,直线与曲线有两个交
解3:∵点P(2,4)在圆外
∴过点P与圆相切的直线有两条,当斜率存在时,设方程为y-4=k(x-2)
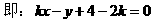
圆心(1,1)
∵圆心到切线的距离等于半径
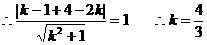
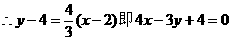
当斜率不存在时,过点P(2,4)的直线为:x=2
∴所求圆的切线方程为:4x-3y+4=0或x=2

例3. (1)已知圆过点P(2,1),与直线x-y=1相切,且它的圆心在直线y=-2x上,求这个圆的方程。
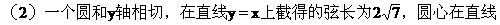
x-3y=0上,求此圆的方程。
解:(1)设所求圆的方程为:(x-a)2+(y-b)2=r2
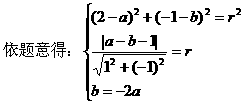
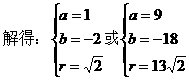
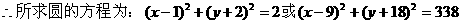
解:(2)设所求圆的方程为:(x-a)2+(y-b)2=r2
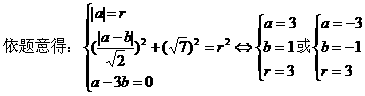
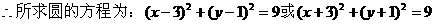
例4. 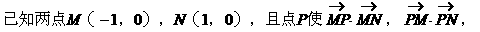
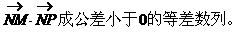
求点P的轨迹。
解:设P(x,y)
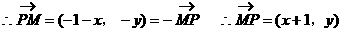
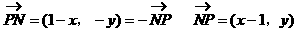
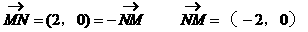
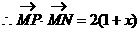
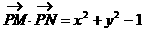
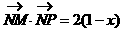
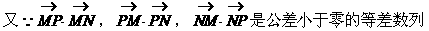
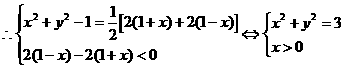
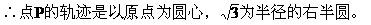
[模拟试题]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com