
题目列表(包括答案和解析)
2.x∈R,那么(1-|x|)(1+x)>0的充要条件是:
A.|x|<1 B.x<1 C.|x|>1 D.x<-1或|x|<1
1.下列命题中,正确的个数为:
①如果a>b,c>d 那么a-d>b-c
②如果a>b,ab>0,则<
③如果a>b>0,c<d<0,则ac<bd
④如果a>b,那么c-2a<c-2b
A.1 B.2 C.3 D.4
17解:设动圆圆心P(x,y)p 半径为r
由已知C1(-3,0) 半径 r1=3 C2(3,0) 半径r2=1
则|PC1|=r1+r=3+r |PC2|=r2+r=1+r
∴|PC1|-|PC2|=(3+r)-(1+r)=2 根据双曲线定义
∴P点为以C1 C2为焦点的双曲线的右支
∴2a=2 a=1 2c=6 c=3 ∴b2=c2-a2=8
所求P点轨迹方程为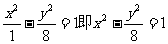 (x>0)
(x>0)
18,解由椭圆几何意义可知,△F1BF2的周长为|BF1|+|BF2|+|F1F2|
即a+a+2C=2a+2C=4+2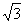 ∴a+c=2+
∴a+c=2+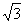 ①
①
∵△F1BF2为等腰三角形,顶角F1BF2=120°∴∠F1BO=60°
∴a=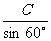 ∴C=
∴C=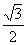 a ②
a ②
由①②可知 a=2 c=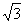 ∴b=1
∴b=1
故所求椭圆方程为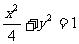 或
或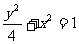
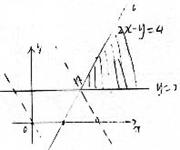 19,解:设所购甲,乙两种食品分别为x, y千克则丙食物为10-x-y千克成本
19,解:设所购甲,乙两种食品分别为x, y千克则丙食物为10-x-y千克成本
 =7x+6y+5(10-x-y)由题意 x, y满足的线性条件
=7x+6y+5(10-x-y)由题意 x, y满足的线性条件
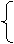 为400x+600y+400(10-x-y)≥4400 即 y≥2
为400x+600y+400(10-x-y)≥4400 即 y≥2
800x+200y+400(10-x-y) ≥4800 2x-y≥4
目标函数 =7x+6y+5(10-x-y)=2x+y+50
=7x+6y+5(10-x-y)=2x+y+50
作出上述不等式所确定的平行或如图令2x+y=m 则直线2x+y=m经过平行域中的A点时m最小
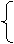 而 y=2
而 y=2
2x-y=4 得A(3 2) ∴ min=2×3+2+50=58
min=2×3+2+50=58
故甲乙丙三种食品各3千克,2千克,5千克是成本最低,最低成本58元
20、解:设点(x .y)则|CA|-|CB|=±2 根据双曲线定义可知点C的轨迹方程为双曲线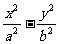 =1 由2a=2 a=1 2C=|AB|=2
=1 由2a=2 a=1 2C=|AB|=2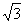 ∴C=
∴C=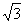 ∴b2=2 故C点轨迹方程为x2-
∴b2=2 故C点轨迹方程为x2-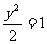
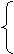 由x2-
由x2-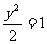
y=x-2 得x2+4x-6=0 ∵△=42+4×6>0 ∴直线与曲线有两交点
设D(x1,y1) E(x2 y2) 则x1+x2=-4 x1·x2=-6 故
|DE|=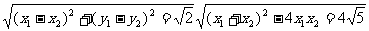
|
 21、解(1)设A(x1,y1) B(x2, y2)则 y=kx+1
21、解(1)设A(x1,y1) B(x2, y2)则 y=kx+1
3x2+y2=1
由韦达定理 x1+x2=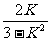 x1·x2=
x1·x2=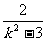 则y1y2=(kx1+1)(kx2+1)
则y1y2=(kx1+1)(kx2+1)
=k2x1x2+k(x1+x2)+1=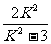 +K·
+K· 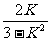 +1=1 又AB为直径的圆过原点
+1=1 又AB为直径的圆过原点
∵DA⊥OB ∴ x1x2+y1y2=0 即 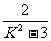 +1=0 K=±1
+1=0 K=±1
(2)假设存在实数使A B两点关于y=2x对称, 则AB中点在y=2x上
由(1)可知中点M(±1 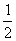 ) ∴
) ∴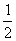 =2·
=2·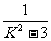 即K=±
即K=±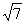
而AB与y=2x垂直∴KAB=-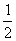 与K=±
与K=±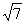 矛盾故假设不成立
矛盾故假设不成立
∴不存在实数K满足上述条件
8、过椭圆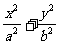 =1(a>b>0)中心的直线与椭圆交于A,B两点,设椭圆焦点分别为F1(-c,0),F2(c,0),则四边形面积最大值( )
=1(a>b>0)中心的直线与椭圆交于A,B两点,设椭圆焦点分别为F1(-c,0),F2(c,0),则四边形面积最大值( )
A ab B 2ab C bc D 2ab
9,如果椭圆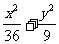 =1的弦被点(4,2)平分,那么这条弦所在直线的方程是( )
=1的弦被点(4,2)平分,那么这条弦所在直线的方程是( )
A x-2y =0 B x+2y-4=0 C 2x+3y-12=0 D x+2y-8=0
10,我国发射的神州号宇宙飞船的运行轨道是以地心为一个焦点的椭圆,设地球的半径为R,飞船的近地点,远地点距地面分别为r1,r2,则飞船运行轨迹短轴长为 ( )
A 2r1r2 B r1r2 C2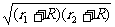 D
D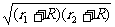
二,填空题(共四小题,每小题4分,共16分)
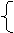 13,曲线x=2cosθ 上的点到直线4x+3y-12=0的距离最大值_____________
13,曲线x=2cosθ 上的点到直线4x+3y-12=0的距离最大值_____________
Y=2sinθ
14,设F1,F2是双曲线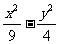 =1的焦点,AB是过左焦点F1的弦,且A,B两点都在左支上,若△ABF2的周长为30,则|AB|_________________
=1的焦点,AB是过左焦点F1的弦,且A,B两点都在左支上,若△ABF2的周长为30,则|AB|_________________
15,若椭圆两准线间的距离等于焦距的4倍,则椭圆的离心率为_________
16经过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的两个交点且面积最小的圆的方程________________
三解答题(共五个大题,64分)
17:(12分)一动圆与两定圆C1:(x+3)2+y2=9和C2:(x-3)2+y2=1都外切,求动圆圆心p的轨迹方程。
18;(12分)已知椭圆中心在原点,对称轴为坐标轴,椭圆短轴端点B与两焦点F1,F2组成三角形的周长为4+2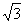 且∠F1BF2=120°,求椭圆的方程。
且∠F1BF2=120°,求椭圆的方程。
19;(12分)下表给出甲,乙,丙三种食物中维生素A,B的含量及成本
|
|
甲 |
乙 |
丙 |
|
维生素A(单位/千克) |
400 |
600 |
400 |
|
维生素B(单位/千克) |
800 |
200 |
400 |
|
成本(元/千克) |
7 |
6 |
5 |
营养师想买这三种食物共10千克,使之所含维生素A不少于4400单位,维生素B不少于4800单位,问这三种食物各购买多少时,成本最低,最低成本是我少?
20:(14分)已知点A(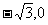 )B(
)B(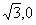 ),动点C到A,B两点的距离的差的绝对值为2,点C的轨迹与直线y=x-2交于D, E两点,求线段DE的长
),动点C到A,B两点的距离的差的绝对值为2,点C的轨迹与直线y=x-2交于D, E两点,求线段DE的长
21:(14分)直线y=kx+1与双曲线3x2-y2=1相交于不同的两点A,B
(1) 若以AB为直径的圆恰好过原点,求k的值
(2) 是否存在实数k,使A,B两点关于直线y=2x对称,若存在求k 的范围,若不存在,说明理由。
高二数学其中考试实验班答案
1, 直线2x-y=0与x-3=0的夹角为( )
A arctan2
B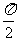 -arctan2 C
arctan
-arctan2 C
arctan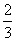 D
D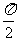 -arctan
-arctan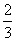
2, 不等式(x3-1)(x -1)(x+2)>0 的解集( )
A {x|x>-2} B{x|x>-2且x≠1}
C{x|x<-2或x>1} D{x|-2<x<1}
3,若直线x+ay-2=0,与(3a-1)x-ay-1=0平行,则a的值为( )
A6 B 1/6 C 0或6 D 0或1/6
4,若0<a<1,0<b<1则 a+b,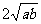 ,a2+b2,2ab中最大的一个是( )
,a2+b2,2ab中最大的一个是( )
A a+b B 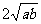 C a2+b2 D 2ab
C a2+b2 D 2ab
5,若图中l1, l2,l3,l4的斜率分别为k1 k2 k3 k4则( )
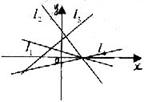 A K3>K4>K2>K1 B K4>K3>K1>K2
A K3>K4>K2>K1 B K4>K3>K1>K2
C K3>K4>K1>K2 D K4>K3>K2>K1
6,点p(x1,y1)关于直线x+y+1=0对称的点的坐标为
( )
A (-y1-1 ,-x1-1) B (y1-1,-x1-1) C (-y1+1,-x1+1) D (y1+1,x1+1)
7、A=C≠0B=0是Ax2+Bxy+Cy2+Dx+Ey+F=0表示圆的( )
A、充分不必要条件 B、必要不充分条件
C、充要条件 D、既不充分又不必要条件
22.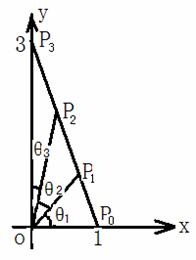 已知两点
已知两点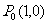 ,
,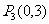 ,
,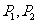 为线段
为线段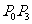 上的两点 设
上的两点 设
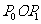 =
=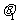 ,
,
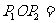
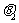 ,
, 
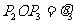 ,
,
①若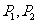 为线段
为线段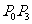 的三等分点,求:
的三等分点,求: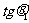 ,
,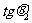 ,
,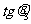 的值;
的值;
②若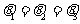 ,求
,求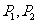 两点的坐标。
两点的坐标。
解:① 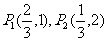
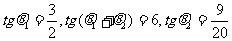
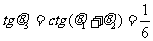
②
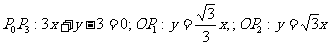
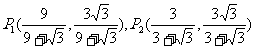
21.某租赁公司拥有汽车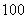 辆,当每辆车的月租金为
辆,当每辆车的月租金为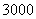 元时,可全部租出,当每辆车的月租金每增加
元时,可全部租出,当每辆车的月租金每增加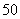 元时,未租出的车将会增加一辆,租出的车每辆每月需维护费
元时,未租出的车将会增加一辆,租出的车每辆每月需维护费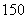 元,未租出的车每辆每月需要维护费
元,未租出的车每辆每月需要维护费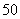 元
元
①当每辆车的月租金定为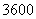 元时,能租出多少辆车?
元时,能租出多少辆车?
②当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
解:① 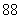 辆
辆
② 月租金定为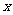 元,月收益为
元,月收益为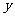 元
元
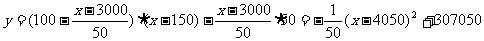
月租金定为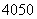 元,最大月收益是
元,最大月收益是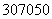 元。
元。
20.已知数列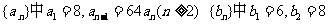 ,前
,前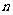 项和
项和

①判断两数列各是什么数列,并求出它们的通项公式;
②能否找到一个不为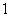 的整数
的整数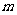 使
使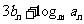 为常数?若找不到,请说明理由;若能找到,试求
为常数?若找不到,请说明理由;若能找到,试求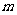 与这个常数。
与这个常数。
解:① 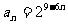 ,
,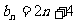
② 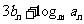
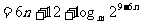 ,
,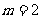 ,
,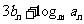
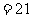
19.正三棱柱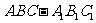 所有棱长均为4,
所有棱长均为4,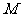 是
是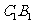 的中点,
的中点,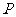 是侧棱
是侧棱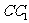 上的一点,
上的一点,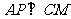
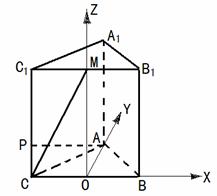 ①建立适当的坐标系,求
①建立适当的坐标系,求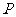 点的坐标;
点的坐标;
②求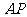 与底面
与底面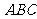 所成角的大小。
所成角的大小。
解:① 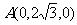
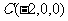
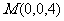
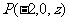
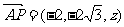
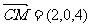
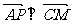
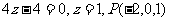
② 
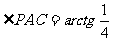
18.有关于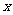 的一元二次方程
的一元二次方程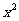 -(
-(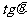 +i)
+i)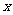 -(2+i)=0(
-(2+i)=0(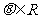 ,
,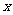
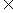
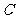 )
)
①若此方程有一实数根,求锐角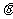 的值;
的值;
②求证:对任意的实数的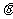 ,原方程不可能有纯虚数根。
,原方程不可能有纯虚数根。
解:① 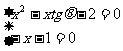 ,
,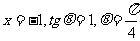
② 设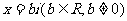 ,则
,则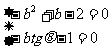 ,
,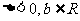
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com