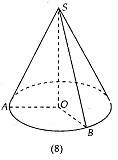
观察图(8)可以看出：它有一个圆面，一个顶点，其他为曲面；可看作是直角△AOS绕其直角边OS旋转而成的．

1、定义

以直角三角形的一条直角边所在直线为旋转轴，其余两边旋转形成的曲面所围成的几何体叫做圆锥．

2、圆柱的记法

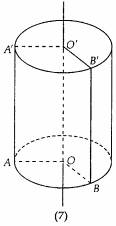
用表示它的轴的字母表示，如图(7)可记为圆柱OO'．

观察图(7)可知：它有两个互相平行的平面，且这两个“平面”是等圆．图形可以看作是矩形AOO'A'绕 OO' 旋转而成的．

1、定义

以矩形的一边所在直线为旋转轴，其余三边旋转形成的曲面所围成的几何体叫做圆柱．

3、棱锥的记法

(1)用顶点和底面各顶点的字母表示．

如图(4)可记为三棱锥P-ABC；图(5)可记为四棱锥P-ABCD；图(6)可记为五棱锥P一ABCDE等．

(2)用对角面表示．

如图(5)可记为四棱锥P-AC；图(6)可记为五棱锥P-AC等．

2、棱锥的分类

底面为三角形、四边形、五边形… …的棱锥分别叫做三棱锥、四棱锥、五棱锥… …，其中三棱锥又叫做四面体．

观察下图，

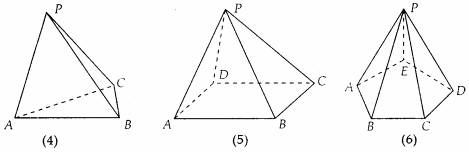
可以看出，上面三个图中的共同特点：

(1)均由平面图形围成；

(2)其中一个面为多边形；

(3)其他各面都是三角形；

(4)这些三角形有一个公共顶点．

1、定义

一般地，有一个面是多边形，其余各面都是有一公共顶点的三角形，由这些面所围成的几何体叫做棱锥．

棱锥是多面体中重要的一种，它有两个本质特征：(1)有一个面是多边形；(2)其余的各面是有一个公共顶点的三角形．两者缺一不可，因此棱锥有一个面是多边形，其余各面都是三角形，但是也要注意：“有一个面是多边形，其余各面都是三角形”的几何体未必是棱锥．

3、棱柱的记法

(1)用表示底面各顶点的字母表示棱柱．

如图(1)可表示为棱柱ABCD-A₁B₁C₁D₁；图(2)可表示为棱柱ABCDEF-A₁B₁C₁D₁E₁F₁；图(3)可表示为棱柱ABCDE－A₁B₁C₁D₁E₁．

(2)用棱柱的对角线表示棱柱．

如图(1)可表示为棱柱AC₁或棱柱BD₁等；图(2)可表示为棱柱AC₁或棱柱AD₁或棱柱AE₁等；图(3)可表示为棱柱AC₁或棱柱AD₁等．

2、棱柱的分类

底面是三角形、四边形、五边形 … … 的棱柱分别叫做三棱柱、四棱柱、五棱柱……

观察下图可以看出，

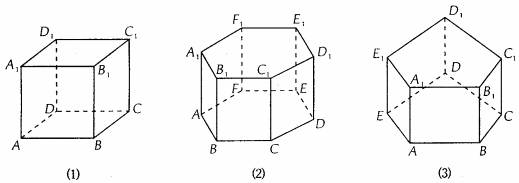
上面各图中都有两个面互相平行，其余各面都是平行四边形．

1、定义

一般地，有两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的几何体叫做棱柱．在棱柱中，两个互相平行的面叫做棱柱的底面，简称底；其余各面叫做棱柱的侧面；相邻侧面的公共边叫做棱柱的侧棱；侧面与底面的公共顶点叫做棱柱的顶点．棱柱中不在同一平面上的两个顶点的连线叫做棱柱的对角线．

19、已知四棱锥P-ABCD的底面是边长为4的正方形，PD⊥底面ABCD，PD=6，M、N分别为PA、PB的中点.

(1) 求证：MN⊥CD.

(2) 求二面角M-DN-C的平面角的正切值.