1、二面角

　　　 (1)从一条直线出发的两个半平面所组成的图形叫做二面角，这条直线叫做二面角的棱，这两个半平面叫做二面角的面，如图所示，即为一个二面角α-l-β。

(2)以二面角的棱上任意一点为端点，在两个面内分别作垂直于棱的两条射线，这两条射线所成的角叫做二面角的平面角，如图所示，若OA⊥l，OB⊥l，则∠AOB是二面角α-l-β的平面角。

说明：

①画二面角的平面角时，使平面角的两边分别平行于表示两个半平面的平行四边形的一组对边，即表明垂直于二面角的棱。

②平面角∠AOB的大小与O点的位置无关。

③二面角的大小是通过它的平面角来度量的，二面角的平面角是多少度，就说这个二面角是多少度，由此可知，二面角的取值范围是。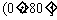

　　　 直线和平面所成的角的定义：平面的一条斜线和它在平面上的射影所成的锐角，叫做这条直线和这个平面所成的角。

　　　 特别地，如果一条直线垂直于平面，我们说它们所成的角为直角；一条直线和平面平行，或在平面内，我们说它们所成的角是0°的角，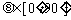

2、性质

　　　 (1)由直线和平面垂直的定义知：直线垂直于平面内的任意直线。

(2)直线与平面垂直的性质定理：垂直于同一平面的两条直线平行。

　　　 用符号可表示为a⊥α，b⊥αa//b。

　　　 说明：性质定理可看成是命题“a⊥α，a//bb⊥α”的逆命题。

1、判定

　　　 (1)利用定义：如果一条直线和一个平面内的任意一条直线都垂直，则此直线与这个平面互相垂直。

(2)可作定理用的命题：如果两条平行直线中的一条垂直于一个平面，那么另一条也垂直于这个平面。

用符号可表示为a//b，a⊥αb⊥α。

(3)直线与平面垂直的判定定理：一条直线与一个平面内的两条相交直线都垂直，那么这条直线就垂直于这个平面。

用符号可表示为。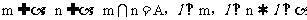

　　　 如果直线l和平面α内的任意一条直线都垂直，我们就说直线l与平面α垂直，记作l⊥α。

　　 和两个平行平面同时垂直的直线，叫做这两个平面的公垂线．公垂线夹在平行平面间的部分．叫做这两个平面的公垂线段．两个平行平面的公垂线段的长度，叫做两个平行平面的距离．

[典例解析]

　 例1. 在正方形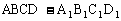中，已知正方体的棱长为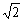，M、N分别在其对角线AD₁与DB上，若AM=BN=x。

　　　 (1)求证：MN//平面CDD₁C₁；

(2)设MN=y，求y=f(x)的表达式；

(3)求MN的最小值，并求此时x的值；

(4)求AD₁与BD所成的角。

　　　 (1)证明：作MP⊥DD₁，NQ⊥CD，连结PQ，如图所示。

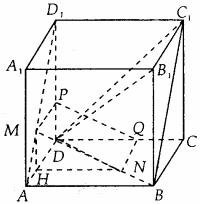
　　　 ∵正方形ADD₁A₁与ABCD有公共边AD，

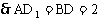
　　　 又∵AM=NB=x，∵D₁M=DN=2－x

　　　 又∵AD⊥DD₁，AD⊥CD，MP⊥DD₁，NQ⊥CD，

　　　 ∵MP//AD//NQ

　　　 ∴D₁M：AD₁=MP：AD，DN：DB=NQ：BC

　　　 ∴MP=NQ

　　　 ∴四边形MNQP为平行四边形

　　　 ∵MN//PQ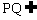，平面DCC₁D₁

　　　 ∴MN//平面DCC₁D₁

　　　 (2)解：作MH⊥AD，连结NH

　　　 ∵MH//AA₁//DD₁，∴AH：HD=AM：MD₁=BN：ND

　　　 ∴HN//AB

　　　 又∵AA₁⊥AB，∴MH⊥HN

　　　 在Rt△MAH中，∠MAH=45°，∴MH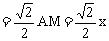

　　　 同理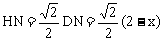

　　　 在Rt△MHN中，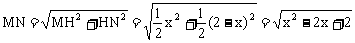

　　　 即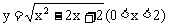

　　　 (3)解：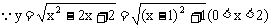

　　　 ∴当x=1时，y有最小值1，即MN的最小值为1。

　　　 (4)解：连结，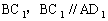

　　　 ∴异面直线AD₁与BD所成的角为DB与BC₁所成的锐角或直角。

　　　 连结C₁D，则△C₁DB为等边三角形，

　　　 即异面直线AD₁与BD所成的角为60°。

　　　 点评：(1)中想证线面平行可利用线线平行，如上面所证，也可通过面面平行来推线面平行，面MNH//面CDD₁C₁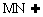，面MNH，∴MN//面CDD₁C₁；

(4)中AD₁与BD所成角不要写成∠C₁BD，而是∠C₁BD或其补角。

　 例2. 如图所示，在棱长为2cm的正方体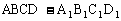中，A₁B₁的中点是P，问过点A₁作与截面PBC₁平行的截面也是三角形吗？求该截面的面积。

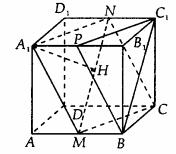
　　　 解：取AB、C₁D₁的中点M、N，连结A₁M、MC、CN、NA₁。由于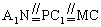，所以四边形A₁MCN是平行四边形。

　　　 又∵，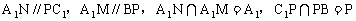

　　　 ∴平面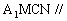平面PBC₁

　　　 因此，过A₁点作与截面PBC₁平行的截面是平行四边形。

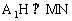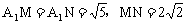　　　 又连结MN，作于H，由于，则。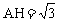

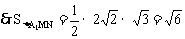
　　　 故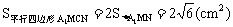

　　 点评：本题是利用面面平行知识解决截面的问题，使我们加深对线面平行、面面平行性质的理解．

专题6　 直线与平面垂直、平面与平面垂直

2、性质

　　　 (1)如果两个平面平行，那么其中一个平面内的直线与另一个平面平行。

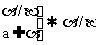
(2)如果两个平行平面都和第三个平面相交，那么它们的交线平行

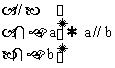
1、判定

　　　 (1)如果一个平面内的两条相交直线都平行于另一个平面，那么这两个平面平行。

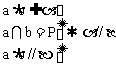
　　　 (2)垂直于同一条直线的两个平面平行，即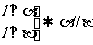

　　　 (3)如果一个平面内有两条相交直线分别平行于另一个平面内的两条直线，那么这两个平面平行。

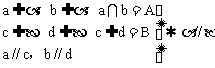
2、两平面相交--有一条公共直线

1、两平面平行--没有公共点