
题目列表(包括答案和解析)
2、公理 4
平行于同一条直线的两条直线平行.它是证明“对应边平行且方向相同的两个角相等”即等角定理的基础,也是论证平行问题的主要根据.
1、定义
同一平面内,两条不相交的直线称为平行直线.
2、若从是否共面的角度看,也可分两类:
(1)在同一平面内--
(2)不同在任一平面内--异面直线.
空间两条不重合的直线有三种位置关系:相交、平行、异面.
1、若从有无公共点的角度看,可分两类
(1)有且仅有一个公共点--相交直线;
(2)没有共点--
2、平面的基本性质
(1)公理 1:对直线 a 和平面α,若点 A、B∈a , A、B∈α,则 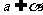
(2)公理 2:若两个平面α、β有一个公共点P,则α、β有且只有一条过点P的公共直线 a。
(3)公理 3及三个推论即为平面的确定条件:
① 不共线的三点可确定一个平面;
② 一条直线和其外一点可确定一个平面;
③ 两条相交直线可确定一个平面;
④ 两条平行直线可确定一个平面.
1、平面的基本特征:无限延展性.
设球半径为R,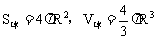
[典例解析]
例1. 已知正四棱锥底面正方形的边长为4cm,高与斜高的夹角为30°,如图,求正四棱锥的侧面积和表面积。(单位: )
)
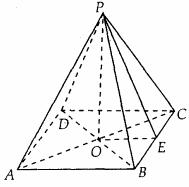
分析:利用正棱锥的高、斜高、底面边心距组成的直角三角形求解,然后代入公式。
解:正棱锥的高PO、斜高PE,底面边心距OE组成Rt△POE。
∵OE=2cm,∠OPE=30°,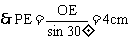
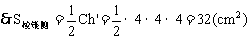
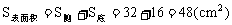
点评:正四棱锥中有四个Rt△,应引起重视,即原题图中Rt△POB、Rt△POE、Rt△PBE、Rt△OBE。
例2. 一个正四棱台两底面边长分别为m、n,侧面积等于两个底面积之和,则这个棱台的高为( )
A.
 B.
B.
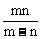 C.
C.
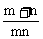 D.
D.
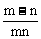
分析:利用直角梯形,转化为直角三角形,结合面积公式求解。
解:如图所示,设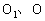 分别为棱台上、下底面中心,
分别为棱台上、下底面中心,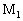 、M分别为
、M分别为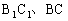 的中点,连结
的中点,连结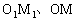 ,则M1M为斜高。
,则M1M为斜高。
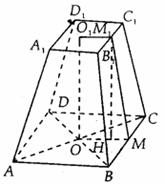
过M1作M1H⊥OM于H点,则M1H=OO1
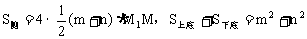
由已知得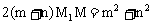
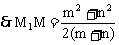
在Rt△M1HM中,MH=OM-O1M1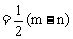
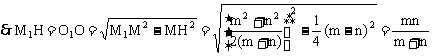
∴应选A。
点评:在正四棱台中有三个直角梯形应注意,一个是O1OMM1,一个是O1OBB1,一个是B1BMM1,它们都可以转化成直角三角形,利用直角三角形求解。
例3. 如图,一个三棱柱形容器中盛有水,且侧棱AA1=8,若侧面AA1B1B水平放置时,液面恰好过AC、BC、A1C1、B1C1的中点,当底面ABC水平放置时,液面高为多少?
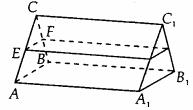
分析:当三棱柱的侧面AA1B1B水平放置时,液体部分是四棱柱,其高为原三棱柱的高,侧棱AA1的长为8。
解:设AC、BC边的中点分别为E、F,设当底面ABC水平放置时,液面高度为h。
由条件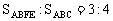 及两种状态下液体体积相等可得
及两种状态下液体体积相等可得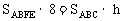 ,∴h=6。
,∴h=6。
点评:等积法是立体几何中的常用方法,在柱、锥中经常通过灵活转换底面,顶点来求高或点到面的距离,应熟练掌握。
例4. (1)用一块矩形铁皮作圆台形铁桶的侧面,要求铁桶的上底半径是24cm,下底半径为16cm,母线长为48cm,则矩形铁皮的长边长最少是多少?
(2)一扇形铁皮AOB,半径OA=72cm,圆心角∠AOB=60°,现剪下一个扇环ABCD作圆台形容器的侧面,并从剩余的扇形COD内剪下一个最大的圆刚好做容器的下底(圆台下底面大于上底面),则OC应取多少?
分析:圆台侧面展开图为一扇环,扇环两弧长分别为圆台上、下底面圆的周长。
解:(1)如图(1),设圆台的侧面展开图的圆心角为∠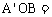 α,OA=x。
α,OA=x。
由相似三角形知识得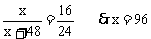
则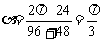 ,
, 为等边三角形。
为等边三角形。
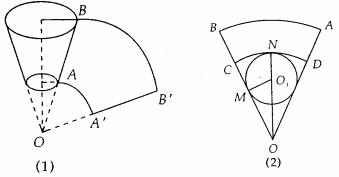
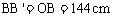 ,即矩形铁皮的长边长最少为144cm。
,即矩形铁皮的长边长最少为144cm。
(2)如图(2),∵∠AOB=60°=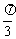
∴圆O1周长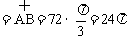 ,即
,即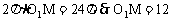
在Rt△O1MO中,∠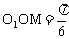 ,∴OO1=2O1M=24
,∴OO1=2O1M=24
点评:注意展开前后有关数学量的变与不变关系,是解决此类问题的突破口。
专题四 空间的平行与异面直线
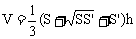 ,其中S为台体的上底面面积,S’为台体的下底面面积,h为台体的高。
,其中S为台体的上底面面积,S’为台体的下底面面积,h为台体的高。
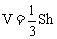 ,其中S为底面积,h为锥体的高。
,其中S为底面积,h为锥体的高。
V=Sh,其中,S为底面积,h为柱体的高。
评注:它既适合于棱柱,又适合于圆柱。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com