2、圆锥的正视图和侧视图都是三角形，俯视图是圆和圆心．

1、圆柱的正视图和侧视图都是矩形，俯视图为圆．

　　 三视图是观察者从不同位置观察同一个几何体，画出的空间几何体图形．

　　 三视图包括正视图、侧视图、俯视图三种．

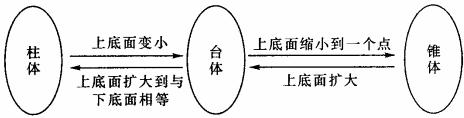
[典例解析]

例1. 下面两图绕虚线旋转一周后形成的立体图形是由哪些简单几何体构成的？

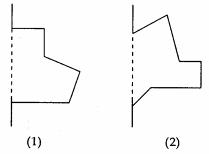
解：旋转后的图形如下图所示

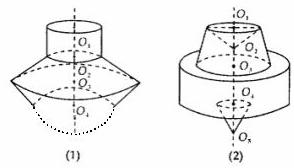
其中(l)由一个圆柱O₁O₂和两个圆台O₂O₃、，圆台O₃O₄组成；(2)由一个圆锥O₄O₅，一个圆柱O₃O₄及一个圆台O₁O₃中挖去圆锥O₁O₂组成．

点评：当一个平面图形绕某条直线旋转后会形成一个旋转体，如直角三角形绕其直角边旋转会形成一个圆锥，矩形绕其一边旋转会形成一个圆柱，直角梯形绕其直角腰旋转会形成一个圆台，半圆绕直径旋转会形成球等．

例2. 请画出如图几个几何体的表面展开图

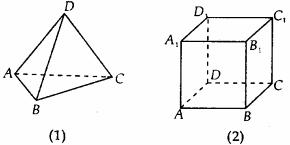
解：展开图如图所示

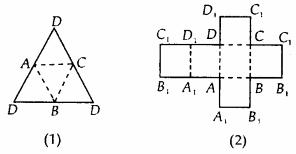
点评：立体图形的展开或平面图形的折叠是我们培养空间立体感的好方法，希望同学们注意这一方面的练习。

专题二　 三视图与直观图

2、球的记法

用表示球心的字母表示，如球O

从图(11)可以看出，此几何体是由半圆绕直径旋转而成的。

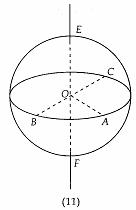
1、定义

以半圆的直径所在的直线为旋转轴，半圆面旋转一周形成的几何体叫做球体，简称球。

3、棱台的记法

(1)用各顶点表示：如四棱台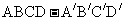

(2)用对角线表示：如四棱台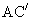

2、圆台的记法

用表示轴的字母表示，如圆台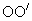

观察图(9)(10)可以看出图形是由平行于底面的平面去截锥体而得到的．

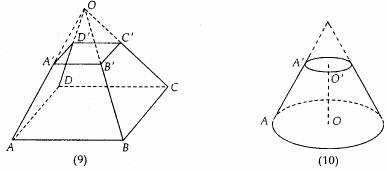
1、定义

用一个平行于棱锥(圆锥)底面的平面去截棱锥(圆锥)，底面和截面之间的部分所构成的几何体叫做棱台(圆台)。

2、圆锥的记法

用表示它的轴的字母表示．如图(8)的圆锥可记为圆锥SO．