
题目列表(包括答案和解析)
7.对于任意x1、x2∈[a,b],满足条件f(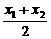 )>
)>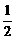 [f(x1)+f(x2)]的函数f(x)的图象是
[f(x1)+f(x2)]的函数f(x)的图象是
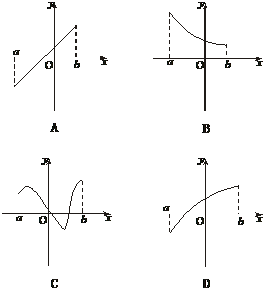
解析:对于A有f(x)为一次函数,显然f(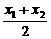 )=
)=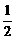 [f(x1)+f(x2)].
[f(x1)+f(x2)].
对于D如下图所示,任取x1<x2,则
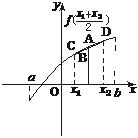
f(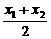 )的值为对应点A的纵坐标,
)的值为对应点A的纵坐标,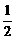 [f(x1)+f(x2)]的值为对应线段CD中点B的纵坐标,显然A在B上方,故选D.
[f(x1)+f(x2)]的值为对应线段CD中点B的纵坐标,显然A在B上方,故选D.
答案:D
6.设f(x)>0是定义在区间I上的减函数,则下列函数中增函数的个数是y=3-2f(x) y=1+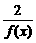 y=[f(x)]2 y=1-
y=[f(x)]2 y=1-
A.1 B.2 C.3 D.4
解析:因为f(x)>0且f(x)在I上是减函数,故y=3-2f(x),y=1+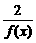 ,y=1-
,y=1- 为I上的增函数,故选C.
为I上的增函数,故选C.
答案:C
5.已知函数f(x)=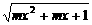 的定义域是一切实数,则m的取值范围是
的定义域是一切实数,则m的取值范围是
A.0<m≤4 B.0≤m≤1 C.m≥4 D.0≤m≤4
解析:要使函数有意义,只需对任意x∈R,不等式mx2+mx+1≥0恒成立.
当m=0时,1≥0,显然成立.
当m≠0时,只需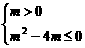
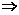
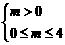
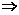 0<m≤4.
0<m≤4.
综上可知,0≤m≤4.
答案:D
4.函数f(x)=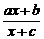 (a、b、c是常数)的反函数是f--1(x)=
(a、b、c是常数)的反函数是f--1(x)=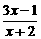 ,则a、b、c的值依次是
,则a、b、c的值依次是
A.2,1,3 B.-2,-1,-3 C.-2,1,3 D.-1,3,-2
解析:由f-1(x)=
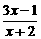 解得f(x)=
解得f(x)=  =
=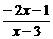 .
.
又f(x)=
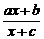 ,∴a=-2,b=-1,c=-3.
,∴a=-2,b=-1,c=-3.
答案:B
3.已知f(x)=3x+1(x∈R),若|f(x)-4|<a的充分条件是|x-1|<b(a、b>0),则a、b之间的关系为
A.a≤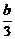 B.b≤
B.b≤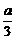 C.b>
C.b>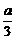 D.a>
D.a>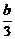
解析:|f(x)-4|<a等价于|x-1|<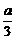 ,
,
由|x-1|<b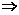 |x-1|<
|x-1|<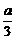 ,
,
∴b≤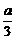 .
.
答案:B
2.函数f(x)=2x2-mx+3,当x∈[-2,+∞)时是增函数,当x∈(-∞,-2]时是减函数,则f(1)等于
A.-3 B.13 C.7 D.由m而定的常数
解析:由题意可知,x=-2是f(x)=2x2-mx+3的对称轴,即-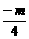 =-2,
=-2,
∴m=-8.∴f(x)=2x2+8x+3.
∴f(1)=13.
答案:B
1.下列各式中,表示y是x的函数的有
①y=x-(x-3);②y= +
+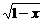 ;③y=
;③y=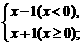 ④y=
④y=
A.4个 B.3个 C.2个 D.1个
解析:①③表示y是x的函数;在②中由 知x∈
知x∈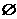 ,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
,因为函数定义域不能是空集,所以②不表示y是x的函数;在④中若x=0,则对应的y的值不唯一,所以④不表示y是x的函数.
答案:C
19.(本小题满分12分)某种细菌每隔两小时分裂一次(每一个细菌分裂成两个,分裂所需时间忽略不计),研究开始时有两个细菌,在研究过程中不断进行分裂,细菌总数y是研究时间t的函数,记作y=f(t).
(1)写出函数y=f(t)的定义域和值域;
(2)在所给坐标系中画出y=f(t)(0≤t<6)的图象;
(3)写出研究进行到n小时(n≥0,n∈Z)时,细菌的总数有多少个(用关于n的式子表示).
解:(1)y=f(t)定义域为t∈[0,+∞),
值域为{y|y=2n,n∈N*}.
(2)0≤t<6时,为一分段函数
y=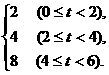
图象如下图.
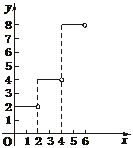
(3)n为偶数时,y=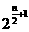 ;
;
n为奇数时,y=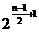 .
.
∴y=
18.(本小题满分12分)设f(x)=lg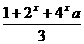 ,且当x∈(-∞,1]时f(x)有意义,求实数a的取值范围.
,且当x∈(-∞,1]时f(x)有意义,求实数a的取值范围.
解:欲使x∈(-∞,1]时,f(x)有意义,需1+2x+4xa>0恒成立,也就是a>
-[(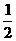 )x+(
)x+(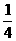 )x](x≤1)恒成立.
)x](x≤1)恒成立.
∵u(x)=-[(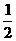 )x+(
)x+(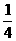 )x]在(-∞,1]上是增函数,
)x]在(-∞,1]上是增函数,
∴当x=1时,[u(x)]max=-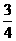 .
.
于是可知,当a>-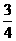 时,满足题意,
时,满足题意,
即a的取值范围为(-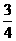 ,+∞).
,+∞).
17.(本小题满分12分)试讨论函数f(x)=loga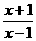 (a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
(a>0且a≠1)在(1,+∞)上的单调性,并予以证明.
分析:本题考查复合函数单调性的判定方法,判定的法则是同增异减,判定的关键是分清函数的复合过程.
解:设u=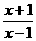 ,任取x2>x1>1,则
,任取x2>x1>1,则
u2-u1=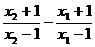
=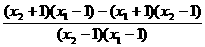
=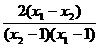 .
.
∵x1>1,x2>1,∴x1-1>0,x2-1>0.
又∵x1<x2,∴x1-x2<0.
∴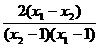 <0,即u2<u1.
<0,即u2<u1.
当a>1时,y=logax是增函数,∴logau2<logau1,
即f(x2)<f(x1);
当0<a<1时,y=logax是减函数,∴logau2>logau1,
即f(x2)>f(x1).
综上可知,当a>1时,f(x)=loga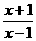 在(1,+∞)上为减函数;当0<a<1时,f(x)=loga
在(1,+∞)上为减函数;当0<a<1时,f(x)=loga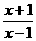 在(1,+∞)上为增函数.
在(1,+∞)上为增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com