
题目列表(包括答案和解析)
3、已知两点P(4,-9),Q(-2,3),则y轴与直线PQ的交点分有向线段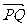 所成的比为( )
所成的比为( )
(A)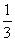 (B)
(B)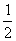 (C)2
(D)3
(C)2
(D)3
2、在四边形ABCD中, 其中
其中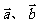 不共线,则四边形ABCD是( )
不共线,则四边形ABCD是( )
(A)梯形 (B)矩形 (C)菱形 (D)正方形
1、下列各式不能化为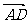 的是( )
的是( )
(A)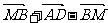 (B)
(B)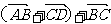
(C)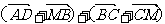 (D)
(D)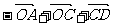
平面向量单元过关检测试卷
24、(本小题满分14分)
将一颗骰子先后抛掷2次,观察向上的点数,问:
(1)两数之和为8的概率;
(2)两数之和是3的倍数的概率;
(3)两数之积是6的倍数的概率。
(4)以第一次向上点数为横坐标x,第二次向上的点数为纵坐标y的点(x,y)在圆x2+y2=25的内部的概率。
解: 将一颗骰子先后抛掷2次,此问题中含有36个等可能基本事件
(1)记“两数之和为6”为事件A,则事件A中含有5个基本事件,所以
P(A)=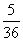 ;
;
答:两数之和为6的概率为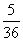 。
。
(2)记“两数之和是3的倍数”为事件B,则事件B中含有12个基本事件,所以
P(B)=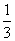 ;
;
答:两数之和是3的倍数的概率为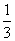 。
。
(3)记“向上的两数之积是6的倍数”为事件C,则事件C中含有其中的15个等可能基本事件,所以
P(C)=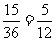 ,
,
答:两数之积是6的倍数的概率为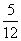 。
。
(4)基本事件总数为36,点(x,y),在圆x2+y2=25的内部记为事件D,则D包含13个事件,
所以P(D)=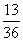 。
。
答:点(x,y)在圆x2+y2=25的内部的概率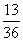 。
。
23、(本题满分12分)设有关于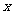 的一元二次方程
的一元二次方程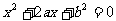 .
.
(1)若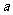 是从
是从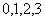 四个数中任取的一个数,
四个数中任取的一个数,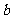 是从
是从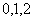 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
(2)若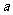 是从区间
是从区间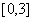 任取的一个数,
任取的一个数, 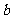 是从区间
是从区间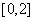 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
解:设事件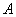 为“方程
为“方程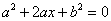 有实根”
有实根”
当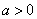 ,
,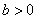 时,方程
时,方程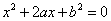 有实根的充要条件为
有实根的充要条件为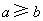
(Ⅰ)基本事件共12个:
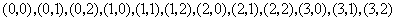 ,其中第一个数表示
,其中第一个数表示 的取值,第二个数表示
的取值,第二个数表示 的取值
的取值
事件A中包含9个基本事件,事件A发生的概率为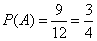
(Ⅱ)试验的全部结束所构成的区域为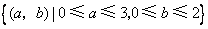
构成事件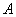 的区域为
的区域为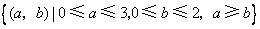
所以所求的概率为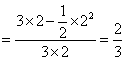
22、(12分) 已知方程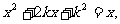 求使方程有两个大于1的实数根的充要条件,并写出它的一个必要不充分条件。
求使方程有两个大于1的实数根的充要条件,并写出它的一个必要不充分条件。
解:分析:△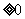 是方程有实数根的充要条件,但只是方程有两个大于1的实数根的必要非充分条件。因此还需结合实根大于1的性质寻求条件组。
是方程有实数根的充要条件,但只是方程有两个大于1的实数根的必要非充分条件。因此还需结合实根大于1的性质寻求条件组。
解:当△=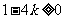 时,方程有两个实数根
时,方程有两个实数根 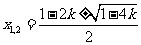 ,
,
所以,方程有两个大于1的实数根的充要条件为:
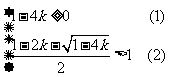
解(1),得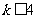 ;解(2),得
;解(2),得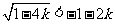 。
。
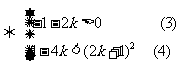
解(3),得 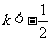 ;解(4),得
;解(4),得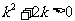 ,即
,即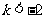 或
或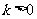 。
。
综合(1),(3),(4)得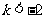 。
。
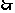 方程有两个大于1的实数根的充要条件是
方程有两个大于1的实数根的充要条件是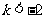 。
。
21、(12分)已知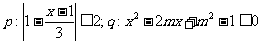 ,且p是q必要不充分条件,求实数m的取值范围。
,且p是q必要不充分条件,求实数m的取值范围。
解: (-1,9)
20、(10分)设x,yÎR,求证:|x+y|=|x|+|y|成立的充要条件是xy³0
19、( 10分)某班有50名学生,在学校组织的一次数学质量抽测中,如果按照抽测成绩的分数段[60,65),[65,70),…,[95,100)进行分组,得到的分布情况如图所示.求:
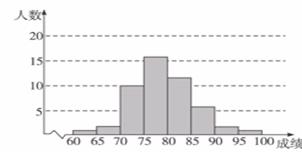
图
(1)该班抽测成绩在[70,85)之间的人数;
(2)该班抽测成绩不低于85分的人数占全班总人数的百分比。
解:从分布图可以看出,抽测成绩各分数段的人数依次为:
[60,65)1人;[65,70)2人;[70,75)10人;[75,80)16人;[80,85)12人;[85,90)6人;[90,95)2人;[95,100)1人.因此,
(1)该班抽测成绩在[70,85)之间的人数为38人.
(2)该班抽测成绩不低于85分的占总人数的18%.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com