
题目列表(包括答案和解析)
4. 如果集合A={x|ax2+2x+1=0}中只有一个元素,则a的值是 ( )
(A)0 (B)0 或1 (C)1 (D)不能确定
3.设函数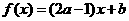 是
是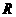 上的减函数,则有 ( )
上的减函数,则有 ( )
A、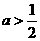 B、
B、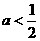 C、
C、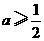 D、
D、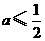
2.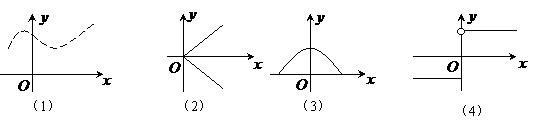 下列四个图像中,是函数图像的是 ( )
下列四个图像中,是函数图像的是 ( )
A、(1) B、(1)、(3)、(4) C、(1)、(2)、(3) D、(3)、(4)
1.已知全集U = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 }, A= {3 ,4 ,5 }, B= {1 ,3 ,6 },
那么集合 { 2 ,7 ,8}是 ( )
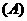

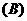
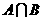

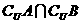
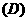
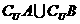
19.(本小题满分12分)已知函数f(x)=(4-3a)x2-2x+a,其中a∈R,求f(x)在[0,1]上的最 大值.
解:(1)当4-3a=0,即a=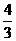 时,f(x)=-2x+
时,f(x)=-2x+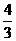 为减函数.所以,f(x)在[0,1]上的最大值为f(0)=
为减函数.所以,f(x)在[0,1]上的最大值为f(0)= 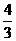 .
.
(2)当4-3a≠0,
即a≠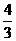 时,f(x)=(4-3a)(x-
时,f(x)=(4-3a)(x-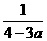 )2+a-
)2+a-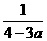 ,
,
此时函数图象的顶点坐标为(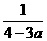 ,a-
,a-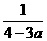 ).
).
①当a>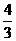 时,4-3a<0,f(x)的图象为开口向下的抛物线,且在[0,1]上递减,
时,4-3a<0,f(x)的图象为开口向下的抛物线,且在[0,1]上递减,
∴[f(x)]max=f(0)=a;
②当a≤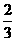 时,0<
时,0<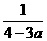 ≤
≤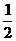 ,f(x)的图象开口向上且顶点横坐标在(0,
,f(x)的图象开口向上且顶点横坐标在(0,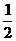 )内,
)内,
∴[f(x)]max=f(1)=2-2a;
③当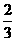 <a≤1时,
<a≤1时,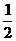 <
< 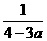 ≤1,f(x)的图象开口向上且顶点横坐标在(
≤1,f(x)的图象开口向上且顶点横坐标在(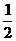 ,1]内,
,1]内,
∴[f(x)]max=f(0)=a;
④当1<a<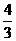 时,
时,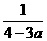 >1,f(x)的图象开口向上,且f(x)在[0,1]上递减,
>1,f(x)的图象开口向上,且f(x)在[0,1]上递减,
∴[f(x)]max=f(0)=a.
18.(本小题满分12分)某家电企业根据市场调查分析,决定调整产品生产方案,准备每周(按120个工时计算)生产空调、彩电、冰箱共360台,且冰箱至少生产60台.已知生产这些家电产品每台所需工时和每台产值如下表:
|
家电名称 |
空调 |
彩电 |
冰箱 |
|
每台所需工时 |
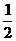 |
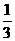 |
 |
|
每台产值(千元) |
4 |
3 |
2 |
问每周应生产空调、彩电、冰箱各多少台,才能使周产值最高?最高产值是多少?(以千元为单位)
解:设每周生产空调、彩电、冰箱分别为x台、y台、z台,每周产值为f千元,
|
其中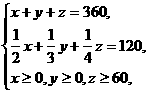
由①②可得y=360-3x,z=2x,
代入③得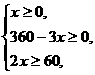 则有30≤x≤120.
则有30≤x≤120.
故f=4x+3(360-3x)+2·2x=1080-x,
当x=30时,fmax=1080-30=1050.
此时y=360-3x=270,z=2x=60.
答:每周应生产空调30台,彩电270台,冰箱60台,才能使每周产值最高,最高产值为1050千元.
17.(本小题满分10分)已知函数f(x)=x2-4ax+2a+30,
(1)求对一切实数x,f(x)的值均为非负实数的充要条件;
(2)在(1)的条件下,求方程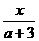 =|a-1|+1的根的取值范围.
=|a-1|+1的根的取值范围.
解:(1)依题意,f(x)≥0恒成立的充要条件是
Δ=(-4a)2-4(2a+30)=16a2-8a-120≤0,解得-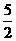 ≤a≤3即为所求.
≤a≤3即为所求.
(2)依题意得x=(a+3)(|a-1|+1)=
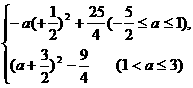
当-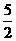 ≤a≤1时,
≤a≤1时,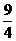 ≤x≤
≤x≤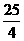 ;当1<a≤3时,4<x≤18.综合得
;当1<a≤3时,4<x≤18.综合得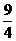 ≤x≤18.
≤x≤18.
16.(本小题满分10分)求函数y=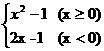 的反函数.
的反函数.
解:当x≥0时,y≥-1,
由y=x2-1,得x=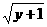 (y≥-1),
(y≥-1),
故y=x2-1(x≥0)的反函数是y=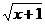 (x≥-1);
(x≥-1);
当x<0时,y<-1,
由y=2x-1得x=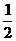 (y+1)(y<-1),
(y+1)(y<-1),
故y=2x-1(x<0)的反函数是y=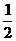 (x+1)(x<-1).
(x+1)(x<-1).
∴f-1(x)=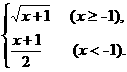
15.(本小题满分10分)某热水贮存器的容量是200升,每分钟放水34升,供应热水的锅炉每t分钟注入贮存器2t2升热水.问贮存器的最小贮存量是多少?如果每人洗浴时用水65升,而贮存器水量达到最小值时放水自动停止,那么这个贮存器一次最多可供几人洗浴?
分析:贮存器内的水量由进水量与原有水量的和减去放水量而得到,求二次函数的最值可用配方法.
解:设贮存器内水量为y升,则由题设有
y=2t2-34t+200=2(t-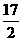 )2+
)2+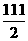 .
.
所以当t=8.5时,贮存器内水量y达到最小值,
此时放水停止.
总共实际放水为8.5×34=289(升).
又289÷65=4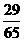 ,所以一次最多可供4人洗浴.
,所以一次最多可供4人洗浴.
14.定义在R上的函数f(x)满足关系式:f(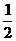 +x)+f(
+x)+f(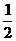 -x)=2,则f(
-x)=2,则f(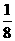 )+f(
)+f(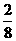 )+…+f(
)+…+f(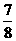 )的值为_______.
)的值为_______.
解析:分别令x=0,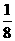 ,
,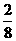 ,
,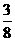 ,
,
由f(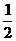 +x)+f(
+x)+f(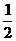 -x)=2,
-x)=2,
得f(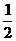 )+f(
)+f(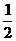 )=2,f(
)=2,f(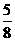 )+f(
)+f(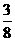 )=2,f(
)=2,f(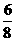 )+f(
)+f(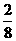 )=2,f(
)=2,f(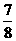 )+f(
)+f(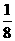 )=2,
)=2,
∴f(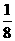 )+f(
)+f(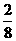 )+…+f(
)+…+f(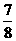 )=7.
)=7.
答案:7
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com