
题目列表(包括答案和解析)
5、已知长方体ABCD-A1B1C1D1的底面ABCD是边长为4的正方形,长方体的高AA1=3,则BC1与对角面BB1D1D所成角的正弦值等于( )
A、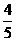 B、
B、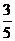 C、
C、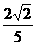 D、
D、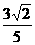
4、(1-x3)(1+x)10的展开式中,x5的系数是( )
A、-297 B、-252 C、297 D、207
3、一个三棱锥S-ABC的三条侧棱SA、SB、SC两两互相垂直且分别为1、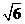 、3,已知该三棱锥的四个顶点都在一个球面上,则这个球的表面积为( )
、3,已知该三棱锥的四个顶点都在一个球面上,则这个球的表面积为( )
A、16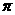 B、32
B、32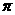 C、36
C、36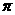 D、64
D、64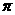
2、将4名教师分配到3所中学任教,每所中学至少1名教师,不同的分配方案共有( )种
A、24 B、36 C、48 D、72
1、设L、m、n是三条不同直线,α、β、γ是三个不同平面,则下列命题不成立的是( )
A、若L⊥α m⊥α 则L∥m
B、若m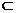 β,n是L在β内的射影 m⊥L 则m⊥n
β,n是L在β内的射影 m⊥L 则m⊥n
C、若m 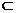 α,n
α,n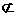 α, m∥n 则n∥α
α, m∥n 则n∥α
D、若α⊥γ β⊥γ 则α∥β
22.(本题满分13分)已知椭圆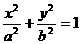 的离心率
的离心率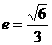 .
.
(Ⅰ)若椭圆准线间的距离为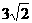 ,求椭圆方程;
,求椭圆方程;
(Ⅱ)直线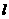 过点C(
过点C(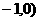 交椭圆于A、B两点,且满足:
交椭圆于A、B两点,且满足: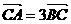 ,试求
,试求 面积的最大值.
面积的最大值.
附加题:(本题解答正确完整给10分,不答或答错不扣分)
有对称中心的曲线叫做有心曲线,显然圆、椭圆、双曲线都是有心曲线. 过有心曲线的中心的弦叫有心曲线的直径,(为研究方便,不妨设直径所在直线的斜率存在).
定理:过圆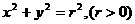 上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-1.
上异于直径两端点的任意一点与一条直径的两个端点连线,则两条连线的斜率之积为定值-1.
(Ⅰ)写出该定理在椭圆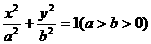 中的推广,并加以证明;
中的推广,并加以证明;
(Ⅱ)写出该定理在双曲线中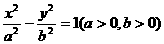 的推广;你能从上述结论得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论.
的推广;你能从上述结论得到有心圆锥曲线(包括椭圆、双曲线、圆)的一般性结论吗?请写出你的结论.
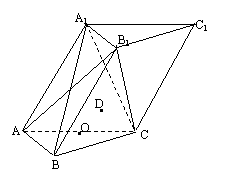
21.(本题满分13分)如图,在各棱长均为2的三棱柱ABC-A1B1C1中,点A1在底面ABC内的射影O恰为线段AC的中点.
(Ⅰ)求侧棱AA1与平面A1BC所成角的正弦值;
(Ⅱ)已知点D为点B关于点O的对称点,在直线AA1上是否存在点P,使DP∥平面AB1C?若存在,请确定点P的位置;若不存在,请说明理由.
20.(本题满分12分)设抛物线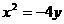 的准线与
的准线与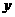 轴的交点为C,过点C作直线
轴的交点为C,过点C作直线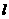 交抛物线于A、B两点,求线段AB中点M的轨迹方程.
交抛物线于A、B两点,求线段AB中点M的轨迹方程.
19.(本题满分14分)如图所示,多面体ABCDS中,面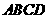 为矩形,SD⊥AD,SD⊥AB,且
为矩形,SD⊥AD,SD⊥AB,且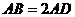 ,
,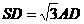 ,
,
M、N分别为AB、CD中点.
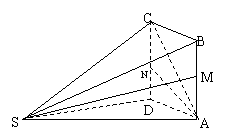 (Ⅰ)求证:SM⊥AN;
(Ⅰ)求证:SM⊥AN;
(Ⅱ)求二面角A-SC-D的余弦值;
(Ⅲ)若AB=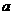 ,求点D到平面ASC的距离.
,求点D到平面ASC的距离.
18.(本题满分12分)已知复数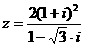 ,
,
(1)求|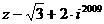 |的值;
|的值;
(2)若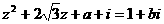 ,求实数
,求实数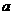 、
、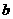 的值.
的值.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com