
题目列表(包括答案和解析)
2.若 、
、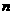 表示直线,
表示直线,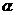 表示平面,则下列命题中,正确的个数为( )
表示平面,则下列命题中,正确的个数为( )
①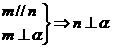 ②
②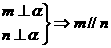 ③
③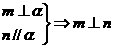 ④
④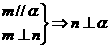
A.1个 B.2个 C.3个 D.4个
1.已知M={正四棱柱},N={长方体},Q={正方体},P={直四棱柱}.则下列关系中正确的是( )
A.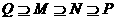 B.
B.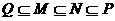
C.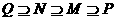 D.
D.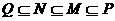
20、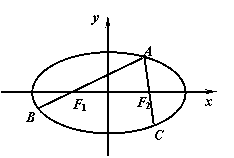 如图,A为椭圆
如图,A为椭圆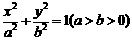 上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
上的一个动点,弦AB、AC分别过焦点F1、F2,当AC垂直于x轴时,恰好有AF1:AF2=3:1.
(Ⅰ) 求椭圆的离心率;
(Ⅱ) 设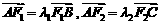 .
.
①当A点恰为椭圆短轴的一个端点时,求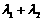 的值;
的值;
②当A点为该椭圆上的一个动点时,试判断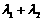 是否
是否
为定值?若是,请证明;若不是,请说明理由.
19、(文科班)设曲线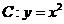 上的点
上的点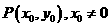 ,过
,过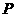 作曲线
作曲线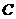 的切线。
的切线。
(1) 若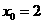 ,求过点
,求过点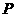 的切线方程;
的切线方程;
(2)设曲线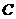 焦点为
焦点为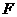 ,切线与
,切线与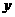 轴交于A,求证:
轴交于A,求证: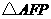 是等腰三角形。
是等腰三角形。
(理科班)在棱长为4的正方体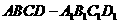 中,
中, 正方形
正方形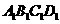 的中心,点
的中心,点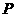 在棱
在棱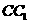 上,且
上,且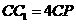 .
.
(1)求直线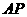 与平面
与平面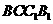 所成角的余弦值;
所成角的余弦值;
(2)设点 在平面
在平面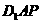 上的射影为
上的射影为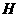 ,求证:
,求证: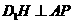 ;
;
(3)求点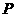 到平面
到平面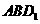 的距离.
的距离.
18、(文科班)已知曲线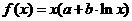 过点P(1,3),且在点P处的切线恰好与直线
过点P(1,3),且在点P处的切线恰好与直线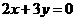 垂直. 求(Ⅰ) 常数
垂直. 求(Ⅰ) 常数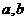 的值; (Ⅱ)
的值; (Ⅱ)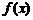 的单调区间.
的单调区间.
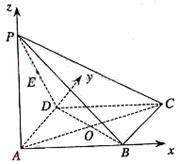
(理科班)如图,在四棱锥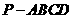 中,底面
中,底面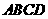 为矩形,侧棱
为矩形,侧棱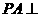 底面
底面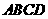 ,
,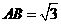 ,
,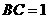 ,
,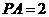 ,
,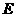 为
为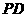 的中点.
的中点.
(Ⅰ)求直线 与
与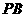 所成角的余弦值;
所成角的余弦值;
(Ⅱ)在侧面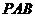 内找一点
内找一点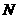 ,使
,使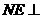 面
面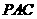 ,并求出点
,并求出点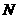 到
到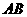 和
和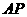 的距离.
的距离.
17、(文科班)同时掷3个骰子。求:(1)三个骰子的点数都是4的概率; (2)三个骰子的点数和小于5的概率。(3)三个骰子的点数至少有两个相同的概率;
(理科班)已知正方形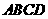 ,边长为2,正方形内任意一点的选取都是等可能的,任选一点
,边长为2,正方形内任意一点的选取都是等可能的,任选一点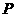 ,作
,作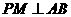 于
于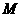 ,
,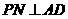 于
于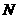 ,矩形
,矩形 的面积为
的面积为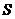 。
。
 (1)请建立适当的坐标系,设
(1)请建立适当的坐标系,设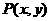 ,作出满足
,作出满足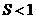 的
的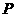 点的区域,并写出
点的区域,并写出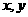 满足的条件;
满足的条件;
(2)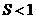 的概率大于0.5吗?试通过计算说明。
的概率大于0.5吗?试通过计算说明。
16、已知双曲线过点P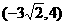 ,它的渐近线方程为
,它的渐近线方程为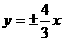
(1)求双曲线的标准方程;
(2)设F1和F2是这双曲线的左、右焦点,点P在这双曲线上,且|PF1|·|PF2|=32,求
∠F1PF2的大小.
15、已知条件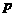 :
: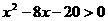 ,
,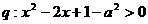 .若
.若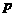 是
是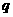 的充分而不必要条件,求正实数
的充分而不必要条件,求正实数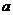 的取值范围.
的取值范围.
14、(文科班)已知函数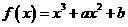 的图象在点
的图象在点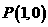 处的切线与直线
处的切线与直线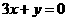 平行,则
平行,则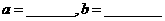 .
.
(理科班)若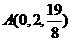 ,
,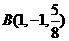 ,
,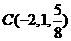 是平面
是平面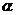 内的三点,设平面
内的三点,设平面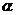 的法向
的法向
量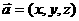 ,则
,则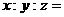 ________________.
________________.
13、分别在区间[1,6]和[2,4]内任取一实数,依次记为m和n,则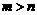 的概率为
.
的概率为
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com