26．解：(1)∵点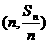在函数y = 3x－2的图象上，

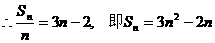　……………………………………3分

∴a₁= s₁ =1

当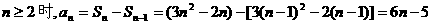

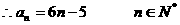　………………………………………… 6分

　 (2)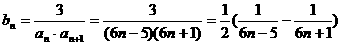　 …………8分

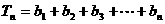
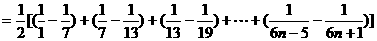
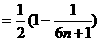
　　 因此，使得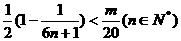成立的m必须且仅需满足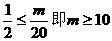，故满足要求的最小整数m为10.……………………12分

25．(Ⅰ)由a_n+2＝2a_n+1－a_nÞ

a_n+2－a_n+1＝a_n+1－a_n，可知{a_n}成等差数列，d＝＝－2

∴a_n＝10－2n．

(Ⅱ)由a_n＝10－2n≥0得n≤5　 ∴当n≤5时，S_n＝－n²+9n，

当n>5时，S_n＝n²－9n+40，

故S_n＝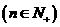　

(Ⅲ)b_n＝＝＝()

∴T_n＝ b₁+b₂+…+b_n

＝[(1－)+(－)+(－)+……+(－)]

＝(1－)＝＞＞T_n－1＞T_n－2＞……＞T₁.　　

∴要使T_n>总成立，需<T₁＝恒成立，即m<8，(m∈Z)．

故适合条件的m的最大值为7．

24、⑴由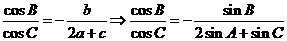

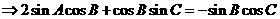
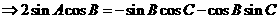
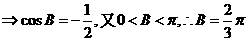
⑵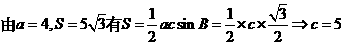

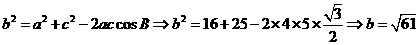
23. (本小题14分)

　 解:　 设A,C分别表示缉私艇,走私船的位置,设经过 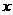　小时后在B处追上,　 则有

,

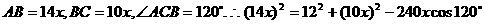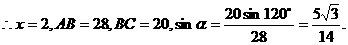
所以所需时间2小时,

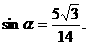
21．解：A = {x|x²－x－6<0} = {x|－2 < x < 3}

　 　B = {x|x² + 2x－8≥0} = {x≤－4或x≥2}………………………………… 2分

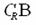
　　 ∴　　　 ={x|－4< x <2}

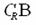
　　 A∩　　 = {x|－2 < x < 2}　 ………………………………………… 4分

又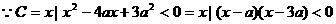

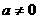
∴当a > 0时，C = {x |a < x < 3a}

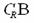　 当a < 0时，C = {x |3a < x < a}………………………………………6分

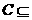∵(A∩　　 )

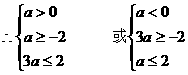　……………………………………………8分

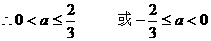　……………………………………………10分

22解：方程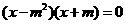的两根为-m<2m²，所以，

　 　①当-m<2m²，即m<-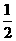或m>0时，原不等式的解集为；

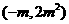　 　②当-m=2m²，即m=0或m=-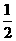时，原不等式的解集为；

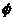　 　③当-m>2m²，即-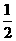<m<0时，原不等式的解集为；

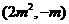20.解: 由题意得 ,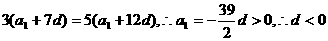

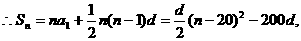
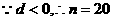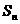时,有最大值.

19. 　()

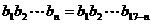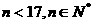13.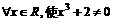 14. 48 　16.18; 17.10;

18.在分式的位置凑出分母x-1，在3x后面施加互逆运算：±3

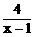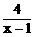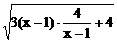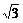原式=(3x-3)+3++1=3(x-1)++4≥2=4+4

1.B; 2.B; 3.B; 4.C; 5.D; 6.A 7.C 8.B 9.C 10.B 11.B12.A

27、设不等式组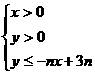所表示的平面区域为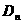，记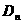内的格点(格点即横坐标和纵坐标均为整数的点)个数为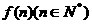

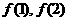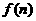(1)求的值及的表达式；

(2)记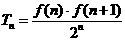，试比较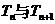的大小；若对于一切的正整数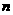，总有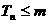成立，求实数的取值范围；

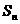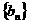(3)设为数列的前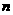项的和，其中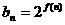，问是否存在正整数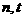，使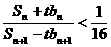成立？若存在，求出正整数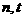；若不存在