
3. 若互不相等的实数a、b、c成等差数列, c、a、b成等比数列,且a+3b+c=10, 则a等于( )
A.4 B.-2 C.2或-4 D.-4
2. 给定两个向量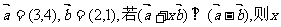 的值等于( )
的值等于( )
A.-3 B.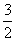 C.3 D.
C.3 D.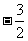
1. 已知角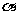 的终边过点P(-8m, -6sin30°),且cos
的终边过点P(-8m, -6sin30°),且cos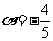 ,则m的值为( )
,则m的值为( )
A.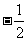 B.
B.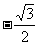 C.
C. 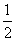 D.
D. 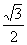
22.(本小题满分14分)
已知函数f(x)=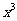 -
-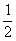 x2+bx+c.
x2+bx+c.
(1)若f (x)有极值,求b的取值范围;
(2)当f (x)在x=1处取得极值时,①若当x∈[-1,2]时,f (x)<c2恒成立,求c的取值范围;②证明:对[-1,2]内的任意两个值x1,x2,都有|f (x1)-f (x2)|<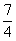 .
.
21.(本小题满分12分)
某地区的一种特色水果上市时间能持续5个月,预测上市初期和后期会因供不应求使价格呈连续上涨态势,而中期又将出现供大于求使价格连续下跌,现有三种价格模拟函数:
①f(x)=p·qx;
②f(x)=logqx+p;
③f(x)=(x-1)(x-q)2+p(以上三式中p、q均为常数,且q>2).
(1)为准确研究其价格走势,应选哪种价格模拟函数,为什么?
(2)若f (1)=4, f (3)=6,(1)求出所选函数f (x)的解析式(注:函数的定义域是[1,6].其中x=1表示4月1日,x=2表示5月1日,…,以此类推);(2)为保证果农的收益,打算在价格下跌期间积极拓宽外销,请你预测该水果在哪几个月内价格下跌.
20.(本小题满分12分)
已知各项均为正数的数列{an}前n项和为Sn,首项为a1,且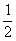 ,an,Sn成等差数列.
,an,Sn成等差数列.
(1)求数列{an}的通项公式;
(2)若an2=(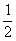 )bn,设cn=
)bn,设cn=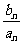 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.
19.(本小题满分12分)
若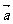 =
=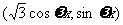 ,
,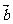 =
=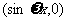 ,其中
,其中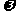 >0,记函数f(x)=(
>0,记函数f(x)=(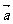 +
+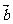 )·
)·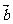 +k.
+k.
(1)若f(x)图象中相邻两条对称轴间的距离不小于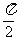 ,求
,求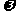 的取值范围.
的取值范围.
(2)若f(x)的最小正周期为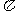 ,且当x
,且当x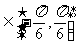 时,f(x)的最大值是
时,f(x)的最大值是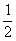 ,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象.
,求f(x)的解析式,并说明如何由y=sinx的图象变换得到y=f(x)的图象.
18.(本小题满分12分)
已知命题p: x(6-x)≥-16,命题q:x2+2x+1-m2≤0(m<0),若┓p是┓q的必要条件,求实数m的取值范围.
17.(本小题满分12分)
在△ABC中,a、b、c分别为∠A、∠B、∠C的对边,若a、b、c成等差数列,sinB=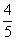 且△ABC的面积为
且△ABC的面积为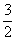 ,求b.
,求b.
16.设函数f(x)=sin(ωx+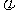 )(ω>0,
)(ω>0,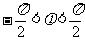 ),给出以下四个论断:
),给出以下四个论断:
①它的周期为π;②它的图象关于直线x=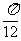 对称;
对称;
③它的图象关于点(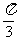 ,0)对称;④在区间(
,0)对称;④在区间(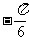 ,0)上是增函数.
,0)上是增函数.
以其中两个论断为条件,另两个论断作结论,写出你认为正确的一个命题:
__________________________________________(注:填上你认为正确的一种答案即可).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com